昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
引用 寒湘子 的回复内容：
……
函数…定义域是由函数定义和运算规则确定.这在逻辑上是“与”的概念，集合概念是“交集”，而不是刘老师的“并集”那是“或”的概念。
……
1、 “刘老师的“并集”那是“或”的概念。”，请把我的原话或原帖贴出来说话，寒湘子不要这样当面造谣式的发言：
2、是这个例4吧？？？
例4，已知f(x)=1/x+√（x+1），求f(x）的定义域。
略解：x≠0且x+1≧0，
∴f(x）的定义域为[-1，0）∪（0，+∞）
注意：答案一般用区间表示。
我再做一遍：
①函数1/x的定义域是x≠0；
②函数√（x+1）的定义域是x+1≧0；
③这样函数f(x)=1/x+√（x+1）的定义域是
函数1/x的定义域x≠0与函数√（x+1）的定义域x+1≧0的交集：
-1≤x＜0和0＜x
用区间方式表示即：
[-1，0）∪（0，+∞）
3、是寒湘子自己看错了吧？？？
4、那个“交集”本身是“两区间的并集”！
引用 寒湘子 的回复内容：
已知一个圆锥曲线，现用一个平面以不同角度切割圆锥。可以得到圆、椭圆、抛物线、双曲线。这些图形函数表示不相同，怎么讲几何变换会保证函数的类型和性质不变！
1、“几何变换会保证函数的类型和性质不变”， 请寒湘子把我的原话或原帖贴出来说话，寒湘子不要这样当面造谣式的发言；
2、函数图像的变换，与寒湘子说的“几何变换”所得的“圆锥曲线”，是两码事，不能换为一谈，
1）函数图像的变换，指函数图像在坐标系中位置的平移、旋转、翻转，……，
2）举例说幂函数y=x^a，变换后为(ey+b)=(cx+d)^a，令y'=ey+b，x'=cx+d，得y'=x'^a，还是幂函数；
3）所以说函数图像的变换，不改变函数的类型和性质！
3、寒湘子竟然把“初等基本函数图像的变换”，与“平面以不同角度切割圆锥所得圆锥曲线”胡扯在一起，这才真正是“胡扯”！！！
引用 寒湘子 的回复内容：
（7）基本初等函数
幂函数y=x^a(x>0)
指数函数y=a^x(a>0,a不等于1)
对数函数y=loga(x)(a>0,a不等于1)
六个基本三角函数：y=sinx,y=cosx,y=tgx,y=ctgx,y=secx(正割印象中是这样缩写，很多年没用，没有核实）,y=cscx(正割印象中是这样缩写，很多年没用，没有核实）
定义域都在定义时规定，因为表达复杂些不一一写出了，原谅。
上述函数必需按定义来理解，不符合定义就不能直接成为幂函数、指有数函数、对数函数，正弦函数等。
……
1、在讨论基本初等函数时，都给定了一个这种函数的定义式 ，所得讨论结果，例如图像、定义域、值域、性质等，是在定义式下讨论的结果；
2、如果是非定义式的基本初等函数，不能直接套用定义式讨论的结果，可以利用讨论的结果，否则是错误的：
举例说，y=2sinx的值域，可以利用定义式y=sinx讨论的结果值域是[-1，+1]，得出y=2sinx的值域是[-2，+2]；
3、举例说，寒湘子认为定义式y=sinx才是正弦函数，y=2sinx还真不是正弦函数，这种理解是十分错误的！
引用 寒湘子 的回复内容：
……
这个一讲大家都明白，所以刘老师关于函数的运算和代数运算不同，压根就是没有任何道理的。函数值的计算只能依据代数规则！
刘老师定义f(x)=loga(x),当(2然x可以等于2,f(2)=loga(2),刘老师又告诉我们要求f(x)-f(-x)=loga(x)-loga(-x),要么x=2带入得到：
loga（2）-loga（-2），要么就没有实数可以带入这样的表达式。
x=2不能带入，x=-2总可以带入了吧！同样得到：loga（-2)-loga（2）这样的怪胎！x不能用正数、负数和零带入，刘老师怎么还能求出这道题的解！不是无中生有？我有讲错刘老师吗？既使他错了，我也没说他说谎，而只是讲他错了。刘老师为什么说我说谎呢？
1、讨论函数时，第一要做的就是求函数的定义域；
举例说，
5、知道函数f(x)=lg(x-2)+√5-x的定义域是2＜x≤5，即定义区间(2,5]，有什么意义？
1）即x只能取定义区间(2,5]的数，才可以代入函数式f(x)=lg(x-2)+√5-x；
2）如果x取值不在定义区间(2,5]的数，就不可以代入函数式f(x)=lg(x-2)+√5-x；
3）举例说，x=6，不在定义区间(2,5]上，代入函数式
f(x)=lg(x-2)+√5-x=lg(6-2)+√5-6=lg(4)+√-1，
出现√-1，无意义；
4）举例说，x=3，在定义区间(2,5]上，代入函数式
f(x)=lg(x-2)+√5-x=lg(3-2)+√5-3=lg(1)+√2=√2，
函数f(x)=lg(x-2)+√5-x有意义，有确定的值√2；
8、函数式（f(x)-f(-x)）/x的定义域是“空集”，函数f(x)的定义域是x＞0，函数-f(-x)的定义域是x＜0；
1）所以x＞0时，函数式（f(x)-f(-x)）/x没有意义，函数式f(x)/x有意义；
2）所以x＜0时，函数式（f(x)-f(-x)）/x没有意义，函数式-f(-x)/x有意义；
3）我们的结论是，函数式（f(x)-f(-x)）/x是个分段函数，
x＞0时，函数式（f(x)-f(-x)）/x=f(x)/x有意义；
x＜0时，函数式（f(x)-f(-x)）/x=-f(-x)/x有意义；
4）寒湘子所谓“这样的怪胎！x不能用正数、负数和零带入，”，实际上就是求得的函数定义域是个“空集”，正数、负数和零都不是定义域上的数，用正数、负数和零带入当然出错了！
引用 寒湘子 的回复内容：
……随意根据辩论的要求，一会讲两个函数的差是空集，一会又能计算函数的值域，定义域都没有元素，值域怎么会有元素！一会求定义域是“交”一会又是“并”。不是满嘴胡说！可怜啊，刘老师，到了这把年龄，还不能自己相信自己，别人怎么会信！
1、主楼题目函数（f(x)-f(-x)）/x，定义域是“ 空集”，用寒湘子的“数学术语”说是个“怪胎”；
2、但是主楼题目函数式（f(x)-f(-x)）/x是个分段函数，
x＞0时，函数式（f(x)-f(-x)）/x=f(x)/x有意义；
x＜0时，函数式（f(x)-f(-x)）/x=-f(-x)/x有意义；
分段函数的值域是各段函数值域的“并集”
3、“定义域都没有元素，值域怎么会有元素！”，“定义域都没有元素”是针对函数式（f(x)-f(-x)）/x定义域是“空集”，“值域…有元素”是针对它是一分段函数而言的！
4、有一个是胡说的吗？
5、寒湘子自己不懂，不明白，还是装糊涂？？？
6、主楼题目不会解，说是错题，寒湘子真的很可怜！
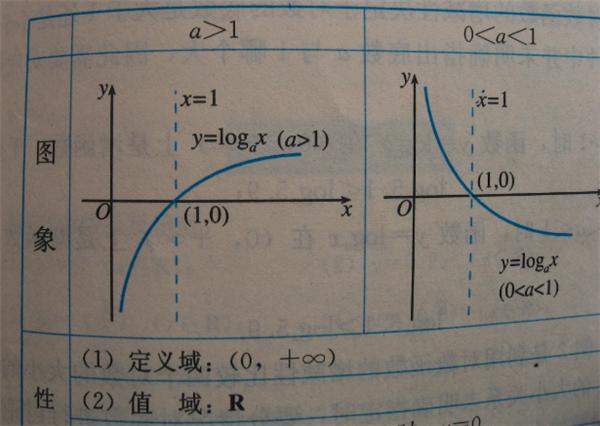
刘志斌把对数函数胡搅到平面直角坐标系的2、3象限，是一个很无知的谬误！
在正统数学理论里，对数函数 y=logax 只能在1、4象限有图象，2、3是绝不能有对数函数 y=logax 的图象的！
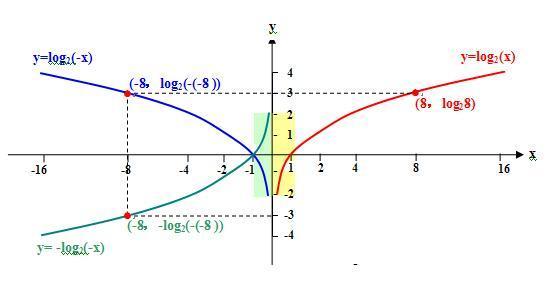
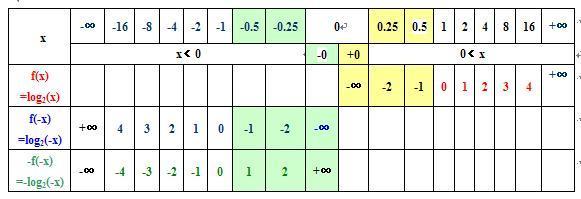
下面的图片和内容是老王在656楼已经说过的：
如果想在1、4和2、3象限同时画出类似对数的函数曲线，那么，这个函数应该是一个“复合函数”！
譬如： u是“x的绝对值” u = φ(x) =│x│ 自变量x取除0之外的一切实数，u按“对应法则”总是正数。正数就有对数！
所以，函数y=logau （u≠0） 是成立的！
∵ u又是x的函数， ∴ y=f(φ(x))＝loga(│x│) 此复合函数当自变量x在除0之外的实数范围内都有意义。
这是老王曾在657楼发表过的图片和内容：
唯有正数才有对数，负数和0没有对数；
除0之外的一切实数的绝对值是正数，所以，除0之外的任何实数之绝对值是有对数的。
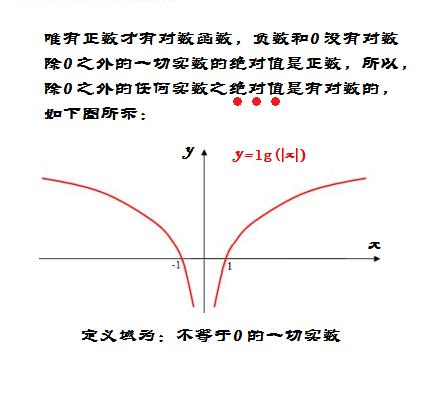
但是，这种关于y轴成轴对称的函数曲线，是不符合楼主题目之题意的！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
