昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
1、这个题目是在哪一个章节出现的题目？如果是在基本初等函数的内容，也可以这样理解：
1）因为f（1）=0，且在0到正无穷大是增函数，所以这个函数可以理解为f(x)=logaX，a＞1；
2）那么函数f(-x)=loga(-X)，a＞1，定义域为0到负无穷大是减函数；
3）这样f(x)-f(-x)是一个分段函数：
当x＞0时，f(x)-f(-x)=f(x)，这样，在区间（0，1）上，f(x)/x<0；
当x＜0时，f(x)-f(-x)= - f(-x)，这样，在区间（-1，0）上，-f(-x)/x<0；
4）图像如图：
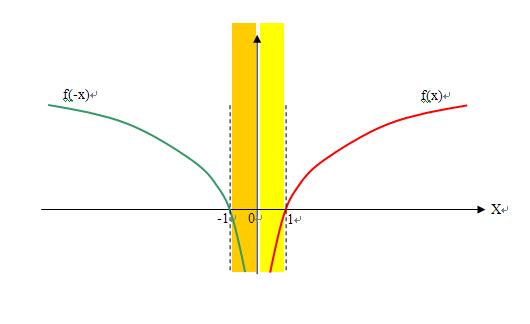
2、这个题目的核心是由f(x)的定义域，求得f(-x)的定义域，再求得分段函数f(x)-f(-x)的定义域；
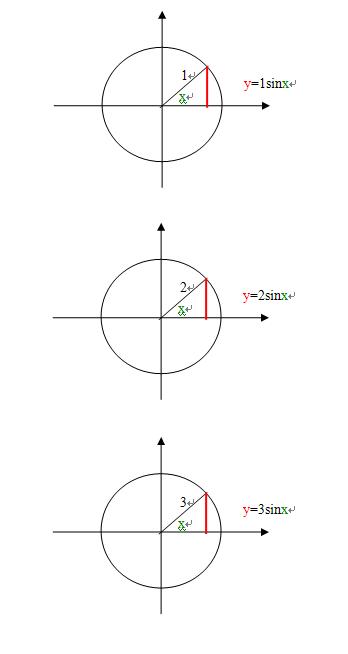
3、就好像sinx是对边y与斜边2的比值，比值sinx与“对边y与斜边2”的大小无关；
4、但是函数值对边y的大小与斜边2的大小是有关的，即y=2sinx；
5、所以y=sinx是正弦函数，是函数值对边y的大小恰好等于比值sinx的情况，而y=2sinx是正弦函数，是函数值对边y的大小等于2sinx的情况；
6、正弦函数值y就是对边，是与斜边R有关的，等于Rsinx，单位园上的6个三角函数只是个特别定义的三角函数，非普遍意义上的所有园上的6个三角函数！
7、 煙雨朦朦 说“y=2sinx真不是正弦函数”是个笑话！
8、2就是斜边，y就是对边，sinx是比值，y=2sinx当然是y对x的正弦函数，
其值域是（-2，+2）！！！
9、就好像1就是斜边，y就是对边，sinx是比值，y=sinx是y对x的正弦函数，
其值域是（-1，+1）一样！！！
刘老师，怎么说呢，“无中生有”的专家！
以下论断，你在题目条件中能够找出来吗？
1）因为f（1）=0，且在0到正无穷大是增函数，所以这个函数可以理解为f(x)=logaX，a＞1；
3）这样f(x)-f(-x)是一个分段函数：
当x＞0时，f(x)-f(-x)=f(x)，这样，在区间（0，1）上，（f(x)-f(-x)）/x<0；
当x＜0时，f(x)-f(-x)= - f(-x)，这样，在区间（-1，0）上，（f(x)-f(-x)）/x<0；
因为f定义为0到无穷大区间上的函数，必然导致f(x)、f(-x)不能都有意义。比如x=2，f(2)有意义，但f(-2)无意义，因为题目并没有讲x<0，f(x)=0。而且将一个一般函数理解为一个特殊函数也是错误的！要不刘老师将结论告诉大家。看是不是符合题意！
引用 煙雨朦朦 的回复内容：
……
题目定义了f(x)也就定义了f(-x)问题是当以f(x)-f(-x)出现时对于同一个x（注意当我们在函数中同时出现x和-x时，x是同一个值）f(x)与f(-x)必然有一个无法确定！
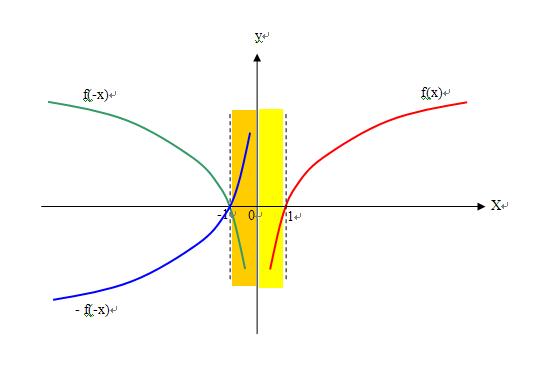
1、题目定义了f(x)，也就定义了f(-x) ，也就定义了-f(-x) ；
2、在（0，+∞）f(x)有意义-f(x)不存在，（-∞，0）f(-x)有意义f(x)不存在，（-∞，0）-f(-x)有意义f(x)不存在；而不是煙雨朦朦说的f(x)与f(-x)必然有一个无法确定！
3、当x＞0时，-f(-x)不存在，所以f(x)-f(-x)就是f(x)；
4、当x＜0时，f(x)不存在，所以f(x)-f(-x)就是- f(-x)；
5、这样当x＞0时，[f(x)-f(-x)]/x，可以理解为f(x)/x，在（0,1）区间上f(x)/x＜0；
6、这样当x＜0时，[f(x)-f(-x)]/x，可以理解为-f(-x)/x，在（-1,0）区间上-f(-x)/x＜0；
7、这个题目只能这样理解了！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
