昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
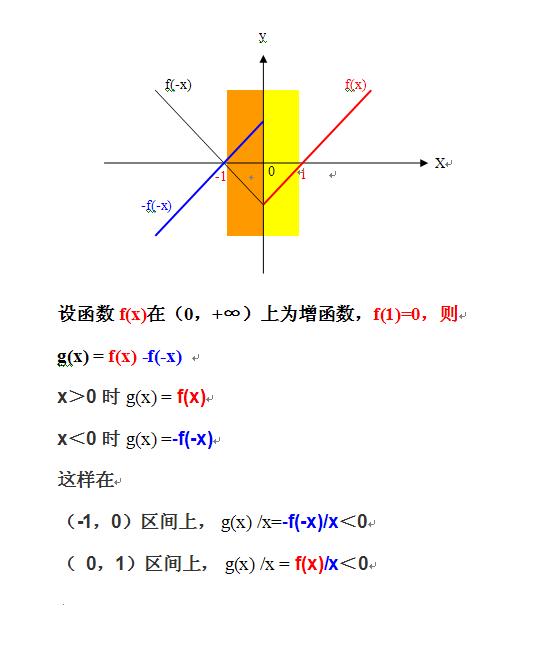
6、寒湘子（煙雨朦朦）最后的补充条件“补充当x<0，f(x)=0；x>0，f(x)是增函数。题目解为：-1<x<0或0<x<1。”，是个什么函数呢？什么函数也不是，是寒湘子（煙雨朦朦）随意编造的，实际上不存在这样的函数！
7、实际上表现出，寒湘子（煙雨朦朦）面对函数f(x)的定义域是x>0，不可理解的样子，他想知道函数f(x)的非定义域x＜0上是个什么？
8、在寒湘子（煙雨朦朦）提出最后的补充条件“补充当x<0，f(x)=0；x>0，f(x)是增函数。题目解为：-1<x<0或0<x<1。”后，不得不承认“分段函数”的存在，“分段函数”的表示方法，恰恰就是对函数不在其定义域上时怎么对待的方式和方法！
引用 寒湘子 的回复内容：
……
对数函数不可能满足原题的要求，原题虽然没有定义x<0 f(x)的属性，但是题目要求求(f(x)-f(-x))/x<0的解集，f(x)和f(-x)必须都有意义，显然对数函数不能满足……
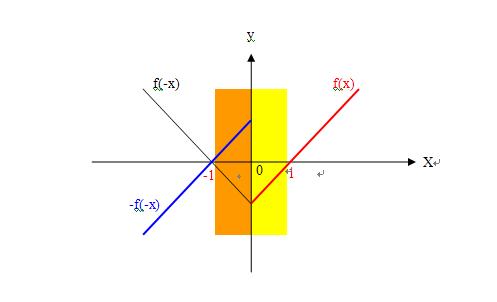
1、“题目要求求(f(x)-f(-x))/x<0的解集 ”，f(x)-f(-x)是一个新的函数，如图
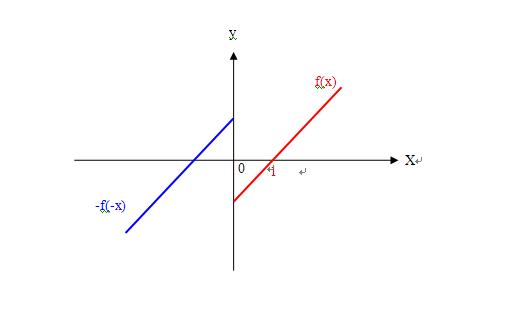
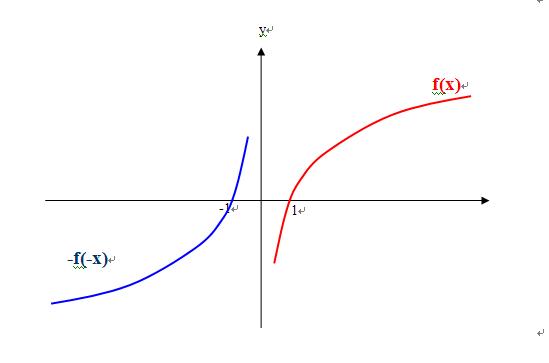
可以表示成分段函数g(x)=f(x)-f(-x)
x＞0时 g(x)=f(x) 是一个增函数，且g(1)=f(1) =0
x＜0时 g(x)=-f(-x) 是一个增函数，且g(-1)=-f(-(-1)) =-f(1)=0
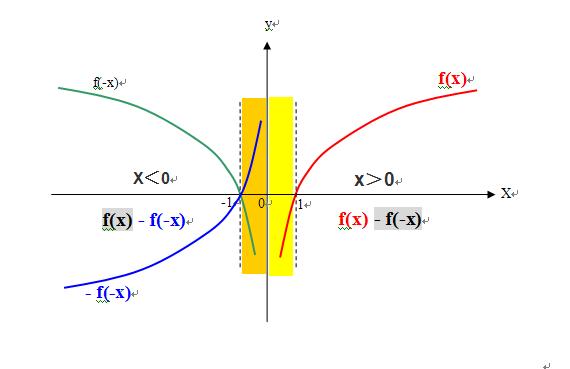
2、一个分段函数表示的就是，在不同的定义区间上有不同定义的函数；
3、“f(x)和f(-x)必须都有意义”，那就不是一个分段函数了；
4、分段函数的定义域，是各段函数定义域的并集；分段函数的值域，是各段函数值域的并集，举例说g(x)=f(x)-f(-x)
x＞0时 g(x)=f(x) 是一个增函数，且g(1)=f(1) =0
x＜0时 g(x)=-f(-x) 是一个增函数，且g(-1)=-f(-(-1)) =-f(1)=0
函数g(x)的定义域就是{x＞0、x＜0}，函数g(x)的值域 {f(x)‖x＞0，-f(-x) ‖x＜0}
引用 寒湘子 的回复内容：
…… 刘老师的观点是对数函数是唯一符合题意的函数！这一点我已反驳！……
1、“刘老师的观点是对数函数是唯一符合题意的函数！” ，寒湘子（煙雨朦朦）这么一说，就歪曲了我的原观点；
2、我说的很清楚，主楼题目出现在教材的那一章节？如果出现在基本初等函数哪一章，满足楼主题设函数f(x)条件的基本初等函数只有对数函数了！
3、我说的很清楚，如果离开题目出现的教材的章节，或者对于对数函数一无所知者，在理解主楼题意时，会联想到其它函数，而其它函数在x＜0时会有意义，会进入思考的“死胡同”，会像寒湘子（煙雨朦朦）那样“绝了至少5种条件下的解集的例子。”，得出“此题条件不足无解”的结论！
4、如果对对数函数的图像熟悉，就不会觉得函数在x＜0时没有定义不可理解！就不会进入思考的“死胡同”，就不会“绝了至少5种条件下的解集的例子。”，得出“此题条件不足无解”的结论！
引用 寒湘子 的回复内容：
……
（2）刘老师声称：做g(x)=f(x)-f(-x),f(x)和f(-x)可以有一个“无意义”或“不存在”，当f(-x)“无意义，g(h)=f(x);当f(x)“无意义”g(x)=-f(-x).这个“刘氏定理”在代数上是不符合代数运算律的！
……
1、说“ 不符合代数运算律”，说明寒湘子（煙雨朦朦）对主楼题意的错误理解；
2、这个题目显然不只是代数运算，是基本初等函数间的运算和复合，是考察对函数概念的掌握、理解、应用解题能力的题目；
3、题目给出函数f(x)，解题时要根据已知函数f(x)推导出函数f(-x)、-f(-x)，进而判断出新函数f(x)-f(-x)的定义域、值域，最终求得答案！
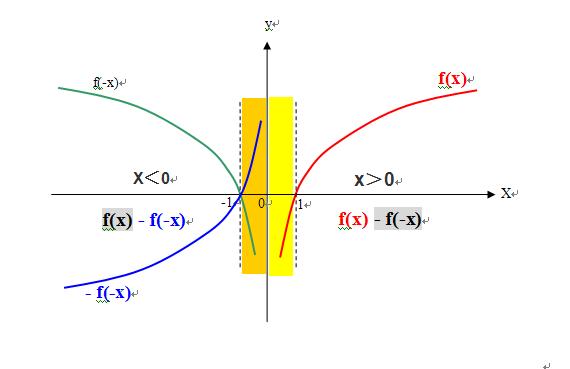
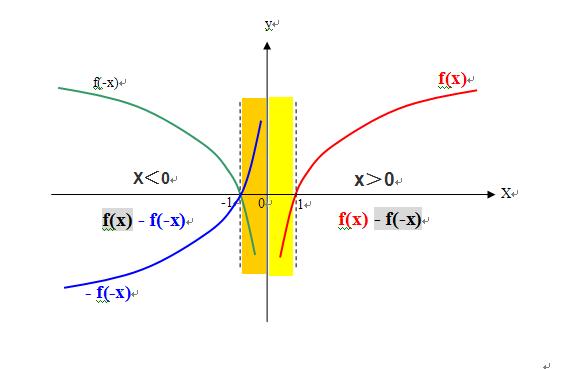
4、举例说：
1）第一步，要根据已知函数f(x)推导出函数f(-x)的定义域、值域、图像；
2）第二步，再根据函数f(-x)推导出函数-f(-x)的定义域、值域、图像；
3）第三步，再求得函数g(x)=f(x)-f(-x)的定义域、值域、图像；
4）最后求得题问的答案；
如图
引用 寒湘子 的回复内容：
这样我和刘老师观点就很清楚了，不要歪曲我的观点。请参阅2楼表述。是刘老师要宣布他可以解出来题目！来反对2楼观点！本来我的看法与他没有任何关系。
还是孔子那句老话：“知之为知之，不知为不知，是知（智）也”，何必自取其辱呢？
一个人不可能什么都懂，自己不懂就不要反对别人了！
“矢量控制真的是谎言吗？”
历史虚无主义，要不得！搞懂了，再说吧！
1、寒湘子（煙雨朦朦）的话，一语道破了这场旷日持久的辩论的原因 ；
2、一道高中的数学题的发言，成为寒湘子（煙雨朦朦）发泄的话题，他千方百计的要证明给大家，对方“…不可能什么都懂…！”
3、企图用“一道高中的数学题”，来证明“矢量控制不是谎言”，也太显得“矢量控制确实是谎言”，竟然荒唐到这种地步需要“一道高中的数学题”的帮助！
4、矢量控制是不是谎言，不是谁说就能算数的，谁说了也不算数，要用“事实”说话！就好像说“鬼”是真的一样，却说不出“鬼”到底是个什么样！？那能是真的吗？
5、寒湘子（煙雨朦朦）的“用心”毫无意义，欺骗“不懂”的人无用，想欺骗“懂”的人那是掩耳盗铃自欺欺人！
我来跟大家一起通过实例来理解一下函数的基本概念：
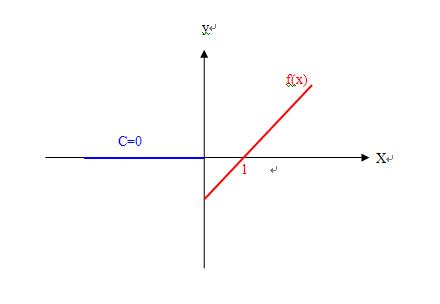
1、举例说主楼题目函数f(x)=logaX，a＞1，loga1=0，定义域为x＞0；
2、那么就有与之以y轴为对称的函数f(-x)=loga(-X)，a＞1，loga(-(-1))=loga1=0，定义域为x＜0；
3、那么就有与f(-x)以x轴为对称的函数-f(-x)=-loga(-X)，a＞1，-loga(-(-1))=-loga1=0，定义域为x＜0；
4、大家看到函数f(x)→函数f(-x)→函数-f(-x)的演变过程中，不变的是f()=loga()，a＞1；
5、我们说函数f(x)、函数f(-x)、函数-f(-x)是同类对数函数，就是说f()=loga()，a＞1是相同的，是没有变的；
6、我们说函数f(x)、函数f(-x)、函数-f(-x)是不同的对数函数，就是说它们的图像位置、定义域、值域不同，自变量x取相反数或者因变量y取相反数；
11、函数f(x)总是在其定义域上有意义，不在其定义域上的函数f(x)怎么理解？
1）不在其定义域上的函数f(x)，能不能说它f(x)=0；
2）不在其定义域上的函数f(x)，只能说它不存在，当然不能认为它f(x)=0；
3）不在其定义域上的函数f(x)，只能说它不存在，是不是还可以研究它是个什么样？
4）不在其定义域上的函数f(x)，只能说它不存在，就是说不用讨论，讨论本身就是错误的；
5）不在其定义域上的函数f(x)，能不能说它不确定？
6）不在其定义域上的函数f(x)，只能说它不存在，而不是不确定，因为不确定就是说还有很多可能；
7）所以分段函数的解析式，在不同定义区间，有不同的表示式，是一个“动”画面，一会儿是云、一会儿是雨、一会儿是太阳、……
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
