有些数学题目的“解”并不是唯一的！

　　譬如说，一元二次方程“Ax^2+Bx+C=0”的解，就有x1, x2 这两个“解”；

　　再譬如说，二元一次方程“x-2y+4=0”的解是一对 一对的实数(x，y)，能够满足等式“x-2y+4=0”的实数对(x，y)有无穷多！

　　例如　(-4，0)；(-2，1)；(2，3)；(4，4)；……等等无穷无尽的实数对，都是二元一次方程“x-2y+4=0”的“解”！

　　在直角坐标平面内，方程“x-2y+4=0”的图象是一条直线，组成这条直线的所有的点(x，y)都是方程“x-2y+4=0”的“解”！

　　楼主的题目所给已知条件“f(x)在0到正无穷大是增函数，f(1)=0”并没有把题设函数f(x)完全框定，所以，题目的“解”就不是唯一的！

　　刘志斌不懂这基本的数学知识，还恶意的对老王的正确观点进行诋毁！

　　下面的截屏图片是刘志斌在230楼恶意的对老王正确观点进行诋毁和胡批的证据：

　　刘志斌荒谬的认为，题目设“f(x)在0到正无穷大是增函数，f(1)=0”那么所设函数f(x)的定义域就必定是“0到正无穷大”。这只能说明刘志斌搞不懂函数的“单调区间”和“定义域”这两个不同概念之间的联系和区别！　

　　在某版本的高中数学教科书上有这样一道习题：证明函数f(x)=x^2-1在[0，+∞)是增函数，且f(1)=0 。

证明：①、设    x1、x2 是[0，+∞)上任意两点，且x1＜x2　,

　　　　　　　则，f(x1)－f(x2)＝(x1)^2-1－(x2)^2+1＝(x1)^2－(x2)^2

　　　　　　　∵　0≤x1＜x2　∴ (x1)^2＜(x2)^2      

　　　　　　　∴   (x1)^2－(x2)^2＜0 　即：f(x1)＜f(x2)

　　　②、当 x=1时， f(1)=(1)^2-1＝0

　　   所以，函数f(x)=x^2-1在[0，+∞)是增函数，且f(1)=0 。

　　倘若刘志斌也因为这高中数学课本上有“函数f(x)=x^2-1在[0，+∞)是增函数，且　f(1)=0 ”便荒谬的妄下断言：“此函数f(x)的定义域为0到正无穷大”，那么，恐怕就真要让高中生们笑掉大牙啦！因为，高中生们都非常的明白：半开区间[0，+∞) 只是函数f(x)=x^2-1的一个“单调区间”而已。

　　高中生们都非常的明白：函数f(x)=x^2-1的定义域是(-∞，+∞)，而不是仅限于半开区间[0，+∞)！ 　

　　题目并没有表示过：所设函数f(x)的定义域是‘在0到正无穷大’！相反的，题目的核心内容“求(f(x)-f(-x))/x＜0时x的范围”还暗示了一个很重要的线索。这个线索告诉我们：题设函数f(x)的定义域并不是仅限于“在0到正无穷大”！它一定延伸到 x＜0的区域！

　　所以，并不是老王给原题目所设函数定义域添加了x＜0的区域！而是题目原本就蕴含着“所设函数f(x)在x＜0的区域也有定义”这一信息的！

　　因为不等式‘(f(x)-f(-x))/x＜0 ’中的一对记号‘f(x) ’和‘f(-x) ’代表的是：当函数的自变量在定义域内取一对互为相反的数值‘x’和‘-x’时分别对应的俩‘函数值’。

　　我们都知道，互为相反的数‘x’和‘-x’必定对称的分布在原点左右两侧，即：互为相反的数必定对称分布在 x＜0 和 x＞0 的两个区域。

　　至于f(x)的定义域向左延伸到多远，题目并没有加以限定！所以，老王所例举的一个分段函数的定义域(-∞，+∞)并不与题设f(x)在0到正无穷大是增函数这一条件相冲突！

　　题目既然没有对f(x)的定义域向左延伸的范围做任何限定，刘志斌又凭什么根据来判定老王所举函数不符合题意呢？！

　　而事实上，老王所举的函数既符合题设‘f(x)在0到正无穷大是增函数，f(1)=0’又有使不等式(f(x)-f(-x))/x＜0  获得“成立”的范围！所以，老王所举的函数f(x)完全符合题意！

　　倘若题设函数f(x)的定义域真如刘志斌所误解的那样仅限于开区间(0，+∞)，那么，这个题目就是一个“无解的题目”！但事实上，<研讨会宣传员-3259>的这个题目所设函数f(x)的定义域并不是仅限于‘在0到正无穷大’（[0,+∞)右半开区间），更不是象刘志斌所误解的：仅限于(0，+∞)开区间！

　　老王所例举的分段函数完全符合题目给出的条件“f(x)在0到正无穷大是增函数，f(1)=0”，并且，还能让题目核心部分的不等式“(f(x)-f(-x))/x＜0”获得成立！

　　但是，刘志斌总是要诋毁和打压辩论对手，愣要把对手所做的正确的题解给胡批成他刘志斌所谓的“错误”！ 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　原题目的题设“f(x)在0到正无穷大是增函数，f(1)=0”并不含有定义域不能超出“单调递增”区间的意涵！相反地，题目在其核心部分却蕴涵了“该函数f(x)的自变量在定义域内可取得互为相反的数的值”这一信息！大家都知道，互为相反的数必定是对称分布在原点两侧的！也就是说题目所指函数f(x)的定义域必定不是仅限于“0到正无穷大”！

　　所以，老王例举的函数在y轴左侧的部分定义域并不是老王违背题意,自己添加补充的！而是题目本来就蕴涵着“f(x)的定义域跨着原点左右两侧”这一信息的！

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　刘志斌把老王所例举的函数经水平翻转，胡搅出另一个根本不符合题意的，映射法则为的函数来！

　　刘志斌这个绕y轴翻转过来的函数根本不符合题意，是因为第1、它的曲线并不经过点(1，0) ，即 f(1)≠0；第2、它的自变量在整个实数范围内都根本不可能使题目核心部分的那个不等式“(f(x)-f(-x))/x＜0”有获得成立的范围！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　本来题目是“求(f(x)-f(-x))/x＜0时x的范围”，可刘志斌却将其胡搅为：“求(刘志斌所谓的)函数f(x)-f(-x)在0到负无穷大区间，”?

　　原题目核心的不等式“(f(x)-f(-x))/x＜0”左边分式的“分子”是同一个函数关系f(x)下的俩函数值之差“f(x)-f(-x)”，刘志斌却将它故意曲解为“函数在0到负无穷大区间”！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　请网友们对照一下老王在所举函数f(x)的定义域内任意列出一组自变量值抽检“题解”符合题意情况的原图内容：

　　在同一个函数(总体层面上的)映射关系下，自变量取一对互为相反的数的值所分别对应的俩函数值“f(x)与f(-x)”之差。

　　譬如：若自变量的取值为x=-2，则函数值f(x)=f(-2)，那么，自变量的取值为

‘-2’的相反数‘2’所对应的函数值即为f(-x)=f(2)。即自变量取一对互为相反的数的值(‘-2’和‘2’)时，分别对应的俩函数值之差为：“f(-2)-f(2)=3.5-1.5＝2”

　　老王再表达得更明白些：

　　把自变量值＜0的区域染成绿色，表示适用分段层次的法则①：y=x^2-0.5 ；

　　把自变量值≥0的区域染成蓝色，表示适用分段层次的法则②：y=0.5x^2-0.5 。

　　通过对照，大家都能看清楚：老王对<研讨会宣传员-3259>的题目的理解是按正统教科书上的理论来理解的：在同一个算式中的符号“f(x)”和“f(-x)”是同一个函数关系下的俩函数值。

　　而刘志斌却是自己瞎胡搅出一套与正统理论相抵触的“刘志斌理论”来曲解的！刘志斌把同一个算式中的符号“f(x)”和“f(-x)”故意曲解为两个不同的“函数”即指坐标平面上两条不同的曲线。

　　刘志斌的曲解，与正统理论是完全抵触的！

　　x是定义域内的任意一个取值，可以取‘-2’，当然也可以取‘2’！我们现在就来看看当自变量值取x=2时的情况：

　　在同一个函数(总体层面上的)映射关系(分段①：y=x^2-0.5   当自变量值＜0；分段②：y=0.5x^2-0.5  当x≥0)之下，自变量取一对互为相反的数的值，所分别对应的俩函数值“f(x)与f(-x)”之差。

　　譬如：若自变量的取值为x=2，则函数值f(x)=f(2)，那么，自变量的取值为‘2’的相反数‘-2’所对应的函数值即为f(-x)=f(-2)。即自变量取一对互为相反的数的值(‘2’和‘-2’)时，分别对应的俩函数值之差为：“f(2)-f(-2)=1.5-3.5＝-2”

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　老王当初贴出的抽检举例图片虽然没有用染色的办法来凸显所例举的分段函数，在定义域的不同区间段对应各分段的对应法则，但仍然是表达得很清楚的：

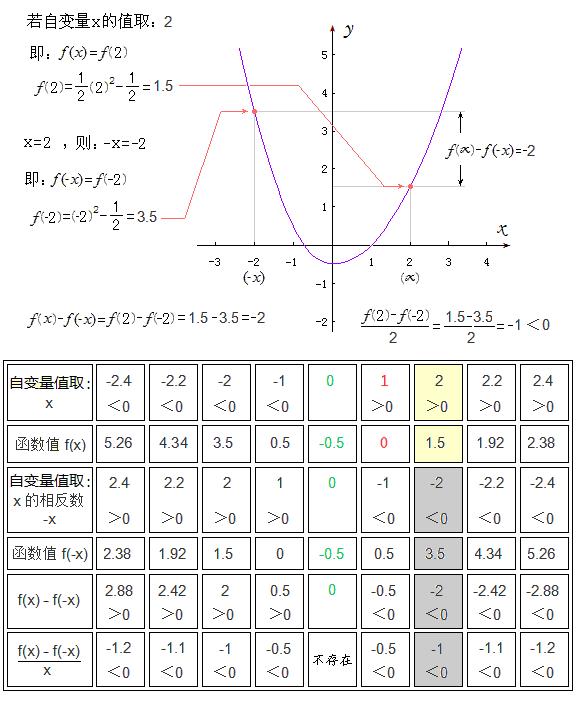
　　这已经是表达得很明白的啦！但是，刘志斌还是故意的将同一个不等式中表示同一个‘函数关系’下的俩函数值符号“f(x)”和“f(-x)”乱搅成“两条不同曲线”各自代表的‘函数’：

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　题目核心:‘求(f(x)-f(-x))/x<0时x的范围’中的符号“f(x)”及“f(-x)”表示同一个函数f(x)（即题设所指的在[0，+∞)区间具有‘单调递增’性质，且f(1)=0，的函数）之自变量分别取互为相反的数“x”及“-x”时，依照函数f(x)的映射法则所对应的“函数值f(x)”及“函数值f(-x)”！

 　　因此，我们在解不等式“(f(x)-f(-x))/x<0”时必须依照同一个函数f(x)的映射法则（对于分段函数来说，就是‘总体层面上的映射法则’）来运算！否则“运算”就是错误的！

　　题目核心内容：“求(f(x)-f(-x))/x<0时x的范围”中的符号“f(x)”及“f(-x)”分明就是同一个函数f(x)（即题设所指的在[0，+∞)区间具有‘单调递增’性质，且f(1)=0 的函数）之自变量分别取互为相反的数“x”及“-x”时，依照函数f(x)的映射法则所对应的“函数值f(x)”及“函数值f(-x)”！但是，刘志斌却恶意的、竭力的否认这不等式中“f(x)”和“f(-x)”之“函数值名份”！

　　下面就是刘志斌恶意否认在同一个不等式中的符号“f(x)”和“f(-x)”之“函数值名分”的截屏证据：

　　刘志斌有什么（可以经得住检验的）凭据说题目核心内容里这个不等式：

‘(f(x)-f(-x))/x＜0’中的符号‘f(x)’和‘f(-x)’不是同一个函数关系下的俩“函数值”？！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　为了针锋相对的反驳刘志斌的谬误言论，老王举例来说明符号‘f(x)’和‘f(-x)’是同一个函数关系下的俩“函数值”！例如，函数y=f(x)=x^2的图象如下：

　　仔细观察函数y=f(x)=x^2的图象，可以看到y=x^2的图象关于y轴对称，从函数

y=f(x)=x^2本身来说，其特点是当自变量取一对相反数时，函数y取同一值.

　　例如，　f(-2)=4， 　　　 f(2)=4，　　    即 f(-2)=f(2)；

　　　　　　f(-1)=1， 　　　 f(1)=1，　　    即 f(-1)=f(1)；

　　　　　　f(-0.5)=0.25，     f(0.5)=0.25 ，  即 f(-0.5)=f(0.5)；

　　　　　　　　　　　　　　　……

　　如果，要象这样用具体的数据来说明函数y=f(x)=x^2当自变量取一对相反数时，函数y取同一值，的这一性质，那是不可能把所有互为相反的自变量值所对应的函数值列举完的！这就需要我们用一个字母来代表自变量在定义域内任意的一个取值！很自然的我们就想到用字母x来代表自变量在定义域内的任意一个取值，而用‘-x’来代表它的相反取值！则，它们分别对应的‘函数值’理所当然的就是‘f(x)’和‘f(-x)’!

　　用符号‘f(x)’和‘f(-x)’表示自变量在定义域内任意的一对互为相反的取值‘x’和‘-x’所分别对应的函数值，实质就是把定义域内无限多对互为相反数分别所对应的函数值之间的数量关系转化为简洁的俩函数值之间的数量关系。

　　由于(-x)^2=x^2 ，所以f(-x)=f(x) . 　请注意，这个等式左右两边的符号‘f(-x)’和‘f(x)’都是同一个函数y=x^2 映射关系下的俩“函数值”！

　　一般地，如果对于函数f(x)的定义域内任意一个x，其相反数-x也在定义域内，且 f(-x)=f(x)，那么函数f(x)就叫做偶函数。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　老王再举例来说明符号‘f(x)’和‘f(-x)’是同一个函数关系下的俩“函数值”！例如，函数y=f(x)=x^3的图象如下： 

　　仔细观察函数y=f(x)=x^3的图象，可以看到y=x^3的图象关于原点对称，从函数

y=f(x)=x^3本身来说，其特点是当自变量取一对相反数时，函数值也得到一对相反数.

　　例如，　f(-2)= -8， 　　　 f(2)=8，　　    即 f(-2)= -f(2)；

　　　　　　f(-3/2)= -27/8，     f(3/2)=27/8，   即 f(-3/2)= -f(3/2)；　

　　　　　　f(-1)= -1， 　　　 f(1)=1，　　    即 f(-1)= -f(1)；

　　　　　　　　　　　　　　　　　　……

　　由于(-x)^3= -x^3，所以f(-x)= -f(x) .  

　　 请网友们注意：这里等式‘ f(-x)= -f(x)’左右两边的‘f(-x)’和‘f(x)’是同一个函数关系“y=f(x)=x^3”下的俩“函数值”！

　　一般地，如果对于函数f(x)的定义域内任意一个x，其相反数-x也在定义域内，且 f(-x)= -f(x)，那么函数f(x)就叫做奇函数。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　老王再举例来说明符号‘f(x)’和‘f(-x)’是同一个函数关系下的俩“函数值”！例如，函数y=f(x)=(x-1)^2 的图象如下：

　　观察函数y=f(x)=(x-1)^2的图象，可以看到y=(x-1)^2的图象既不关于y轴对称，也不关于原点对称。

　　从函数y=f(x)=(x-1)^2本身来说，当自变量取一对相反数时，函数值y既不是同一值，也不是一对相反数.

例如，　f(-2)=9， 　　　f(2)=1，　　    即 f(-2)≠f(2)，　   且f(-2)≠－f(2)；

　　　　f(-1.5)=6.25，    f(1.5)=0.25，   即 f(-1.5)≠f(1.5)， 且f(-1.5)≠－f(1.5)；

　　　　f(-0.5)=2.25，    f(0.5)=0.25 ，  即 f(-0.5)≠f(0.5)， 且f(-0.5)≠－f(0.5)；

……

　　 由于(-x-1)^2≠(x-1)^2，且(-x-1)^2≠ -(x-1)^2 ，所以f(-x)≠f(x)，且f(-x)≠ -f(x) .

 　　请网友们注意：这里的两个不等式‘f(-x)≠ -f(x)’及‘ f(-x)≠f(x)’，其不等号左右两边的‘f(-x)’和‘f(x)’是同一个函数关系“y=f(x)=(x-1)^2”下的俩“函数值”！

 　　一般地，如果对于函数定义域内任意一个x，若有f(-x)≠ -f(x)，且f(-x)≠f(x)，那么函数f(x)既不是奇函数，也不是偶函数！此种情况我们就说函数f(x)不具有奇偶性。  

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　最后再举例说明：当函数f(x)的定义域仅限于原点一侧时，则函数f(x)的值域内不存在‘f(-x)’！

　　例如，函数y=f(x)=ln x 的图象如下：　　　　

　　观察函数y=f(x)=lnx的图象，可以看到y=lnx的图象既不关于y轴对称，也不关于原点对称。

　　在函数f(x)=lnx 的定义域{x│x＞0 }之内，自变量的任意一个取值x，它的相反数‘-x’都落在定义域之外（同理，泛指的f(x)=logax都一样具有这个性质）！

　　所以，对数函数y=f(x)=lnx 、对数函数y=f(x)=lgx 、对数函数y=f(x)=logax ，都不存在‘f(-x)’ ！

　　一般地，如果对于函数定义域内任意一个x，其相反数“-x”都落在定义域之外，那么该函数的值域内就绝无“函数值f(-x)” ! 该函数f(x)也当然的既不是奇函数，也不是偶函数！此种情况当然是函数f(x)不具有奇偶性的情况！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　综上所述，符号‘f(-x)’是“函数值的符号”。“函数值f(-x)”只在函数定义域有互为相反数‘x’和‘-x’的前提下才有存在的意义！

　　请参见正统教科书上关于函数相关知识的论述：

　　f(x)是偶函数的标志是：当自变量x取一对互为相反的数的值时，函数的值不变，就是f(-x)=f(x) 。

　　这里很明显，等式f(-x)=f(x)中的“f(x)”表示当自变量的取值为“x”时对应的“函数值”；而等式中的“f(-x)”则表示当自变量的取值为前者的相反的数值“-x”时对应的“函数值”！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　再参见教科书的这段论述：

　　f(x)是奇函数的标志是：当自变量取一对互为相反的数的值时，函数的值也是互为相反的数，就是f(-x)=－f(x) .

　　这句“函数的值也是互为相反的数，就是f(-x)=－f(x)”非常明确的告诉我们：句中等式‘f(-x)=－f(x)’左右两边的符号‘f(-x)’和‘f(x)’都是同一个函数关系“y=f(x)=x^3”下分别和‘-x’、‘x’相对应的俩“函数值”！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　一般地，对于函数f(x)，要有“x与-x都属于函数的定义域”这个前提，才有谈“f(-x)=f(x)”或“f(-x)=－f(x)”的基础！

　　同理，要有“x与-x都属于函数的定义域”这个前提，才有谈“f(-x)≠f(x)”或

“f(-x)≠－f(x)”的基础！

噢。。。

这个高中数学不但难倒了楼主，也难倒了工控论坛的高手。

您看论战又开始了

　　楼主的这个题目并不怎么‘难’！但是，经刘志斌的一阵胡搅，就把原本是比较简单的概念，搅得混淆不清，让你们分不清原题目的本来意涵，你这才觉得题目有点“难”了！ 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 　　设在一个变化过程中有两个变量x与y，如果对于x在某一范围内的每一个确定的值，y都有唯一确定的值与它对应，那么就称y是x的函数。

　　“y是x的函数”记作：y=f(x)  .　x的函数有时也简记作：f(x) . 

　　在这个记号“f(x)”的括弧中的x叫做自变量，而“f( )”也只是一种记号，它表示因变量y与自变量x之间有某一种映射关系，即对应法则。在不同的函数中对应法则f( )的具体含义不一样。

　　譬如，在函数f(x)=3x中，对应法则f( )就表示“函数值是自变量的3倍”，而在函数f(x)=1/x  (x≠0)中，对应法则f( )就表示“函数值是自变量的倒数”。　

请网友们注意：

　　记号“f(x)”既用来表示函数（例如，“y是x的函数”：y=f(x).），也用来表示“函数值”即自变量在定义域内任意取一值x所对应的“函数值”。

　　而记号“f(-x)”则纯粹是人们在研究讨论函数奇偶性时引入的一个“函数值记号”（例如，我们说奇函数的特点是“当自变量在定义域内取一对儿相反数‘x’、‘-x’时，函数的值也是一对儿互为相反的数”即：f(-x)= -f(x) ）！

　　所以，寒湘子批评：刘志斌把同在一个不等式(f(x)-f(-x))/x＜0中出现的记号f(x)

和f(-x)说成两个函数，这说明(刘志斌)没有弄懂函数的概念。

　　寒湘子所做的这个批评，是完全正确的！我们热烈的鼓掌支持！！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~　　

　　如果要在同一个式子里表示两个不同的函数，就得使用不同的记号来对它们加以区别！这是起码的常识！

　　刘志斌不懂这起码的常识，还夹着屎犟说“1、f(x)和f(-x)是两个函数”！刘志斌自己没有弄懂函数概念，却反讥寒湘子没有弄懂函数概念！

　　寒湘子批评刘志斌时，所指的是题目核心部分那个不等式‘(f(x)-f(-x))/x＜0’中的函数值记号f(x)和f(-x)。这f(x)和f(-x)是同一个函数关系(即同一映射法则)下的俩函数值。

　　而刘志斌却胡搅的用两个不同映射法则的函数：y=x^3  (如下截图中的红色曲线) 和 y=－x^3  (如下截图中的绿色曲线) 来搪塞！　　

　　下面这截屏图片是234楼刘志斌采取胡搅函数概念的贯用手段来搪塞刘自己将题目之不等式中‘f(-x)’曲解为‘有别于题设函数f(x)的另一个函数’这一谬误，所留下的证据：

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~　

　　我们以教科书上的正统理论为依据！请参阅教科书上的这段论述：

　　f(x)是奇函数的标志是：当自变量取一对互为相反的数的值时，函数的值也是互为相反的数，就是f(-x)=－f(x) .

　　这句“函数的值也是互为相反的数，就是f(-x)=-f(x)”非常明确的告诉我们：句中等式‘f(-x)= -f(x)’左右两边的记号‘f(-x)’和‘f(x)’都是同一个函数（譬如，y=f(x)=x^3）映射法则下分别和‘-x’、‘x’相对应的俩“函数值”！

　　用上面的理论依据来分析刘志斌的这条曲线y=f(x)=x^3   ：

　　奇函数、偶函数上所表现的对称性是对一个函数自身曲线分布在y轴左右两侧的两部分而言的，并不是指两个函数的相互对称性 ！

　　刘志斌把表示同一条函数曲线上，位于y轴两侧且与y轴等距离的一对函数值的记号‘f(x)’和‘f(-x)’曲解为“两条曲线”、‘两个不同映射法则的函数’确实显露出刘志斌没有弄懂函数的概念！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

　　用记号‘f(x)’表示函数y=x^3 时，有f(x)=x^3 ，对应法则f( )就表示“函数值是自变量的3次幂”(例如：刘志斌的红色曲线y=f(x)=x^3) ；

　　用记号‘f(x)’表示函数值时，法则记号‘f( )’括弧内的x代表自变量在定义域内任意的某个取值．

　　当需要表示自变量取定义域内任意的一对互为相反数的值所分别对应的俩函数值时，我们分别用‘x’和‘-x’填到记号‘f( )’的括弧内形成对应的俩函数值记号‘f(x)’和‘f(-x)’．

  　请注意：函数值记号‘f(x)’括弧中的内容x是函数定义域内任意的某一取值，所以，x既可以大于0，也可以小于0，还可以等于0．所以，函数值记号‘f(-x)’括弧中的内容‘-x’并不一定代表负数！且括弧中的内容‘-x’的负号也并不代表“映射法则的含义”！它仅仅只是相对于自变量任意的某一取值‘x’而言的相反数的记号而已！

　　‘f(-x)’的映射法则，仍然还是‘f(x)’的映射法则—‘f( )’！以y=x^3为例来说，都是“函数值＝自变量取值的3次幂”！　

　　例如，当x=2时，f(x)=f(2)=2^3=8 ，则f(-x)=f(-2)=(-2)^3＝-8 .

　　很明显：坐标为(2，8)即(2，f(2))的点p在y=x^3曲线上(第1象限)；坐标为(-2，-8)即(-2，f(-2))的点p' 同样的也在y=x^3曲线上(第3象限) ．

　　也就是说，f(x)=x^3与f(-x)=(-x)^3是同一个函数y=x^3 上的俩函数值！刘志斌却恶意的胡搅出一条在2、4象限的绿色曲线来楞充f(-x)=(-x)^3 ，难道在“刘志斌理论”里，点p'(-2，-8) 不在第3象限上？！

　　连高中学生都知道 ，凡横纵坐标皆小于0的点都必定在第3象限！可刘志斌却不懂得这个很基础、很简单的知识！愣要打胡乱说：f(-x)=(-x)^3 不是曲线y=x^3上的函数值（y=x^3曲线上的点p'(-x，f(-x))的纵坐标f(-x)，参见上面的分析图曲线上的p'点）!

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　记号‘f(-x)’原本是人们在研究讨论函数奇偶性问题时引入的一个‘函数值’记号。表示同一函数当自变量取一对儿互为相反数‘x’和‘-x’时，其中‘-x’所对应的‘函数值’。

　　刘志斌弄不懂‘f(-x)’的概念，指鹿为马的把曲线y= -x^3标成“f(-x)=(-x)^3”就堂而皇之的把同一条曲线y=x^3上点p'(-x，f(-x))’的纵坐标‘f(-x)’歪曲成另一条曲线y= -x^3  。却以自己的曲解为“准绳”，迫寒湘子举例来证明这两条不同映射法则的曲线不是两个函数！

　　这里要说明一点：楼主的题目所设的函数f(x)并不是y=x^3，也不是y=-x^3．刘志斌是用这两条不同映射法则的曲线来胡搅题目之不等式“(f(x)-f(-x))/x＜0”中的俩记号‘f(x)’和‘f(-x)’的概念。

　　刘志斌不懂：如果需要在同一个式子中表达不同映射法则的两个函数时，就得把两个不同的映射法则用不同的记号区分开来！譬如，对于函数y=x^3 其法则可采用f( )表示，再对于另一个函数y= -x^3 其法则就可采用另一个记号如g( ) 来表示. 

例如：y=f(x)=x^3  ，y=g(x)= -x^3 

　　记号‘y=g(x)’同样也是表示‘y是x的函数’，x既可以表示正数,也可以表示负数以及0，即：x可以表示自变量在(-∞，+∞)上的任意一个取值。

　　所以，在用记号y=f(x)或记号y=g(x)表示‘y是x的函数’时，完全不需要给自变量名‘x’前加一个负号‘-’！  

 　　只有在函数f(x)定义域内存在有互为相反数‘x’和‘-x’的前提下，当自变量取一对相反数‘x’、‘-x’时，才有分别对应的‘函数值f(x)’和‘函数值f(-x)’。

　　函数值记号‘f(-x)’括弧中的内容‘-x’表示自变量的取值，x前的‘-’号，仅仅只是相对于函数值记号‘f(x)’来说，表示两者各自对应的自变量取值是互为相反的数！‘-x’并不一定代表负数，‘-’号也不代表‘映射法则’！

　　对于函数y=g(x)= -x^3来说，其自变量同样可以取任意一对互为相反的数的值‘x’和‘-x’，那末，这俩自变量值所分别对应的俩‘函数值’就是‘g(x)’和‘g(-x)’! 

　　总之，在同一式子里不论是‘f(x)’与‘f(-x)’组成一对儿也好，或者‘g(x)’与‘g(-x)’构成一对儿也罢，它们都是表示同一函数当自变量取一对儿互为相反的数的值时所分别对应的俩‘函数值’！即同一函数曲线上分处于y轴左右两侧，且与y轴等距离的点的纵坐标。 并不是表示映射法则不同的两个函数！

　“f(x)在0到正无穷大是增函数”仅仅只能说明该函数f(x)在右半开区间 [0，+∞）具有“单调递增”的性质而已！并不是该函数“定义域”的完整信息！因为函数“单调区间”的概念并不等于“定义域”的概念！

　　参见教科书上的练习题：证明二次函数f(x)=ax^2+bx+c  (a＜0)在(-∞,-b/(2a)] 上是增函数．

　　对于这函数f(x)=ax^2+bx+c  (a＜0) 在(-∞,-b/(2a)] 上是增函数．我们都绝不可能将函数f(x)=ax^2+bx+c  (a＜0) 的定义域误解成：“半开区间(-∞,-b/(2a)] ”！

　　因为我们都知道：二次函数f(x)=ax^2+bx+c  (a≠0) 的定义域是(-∞，+∞) !

　　同理，我们都绝不可能把<研讨会宣传员-3259>所给题设“f(x)在0到正无穷大是增函数”误解成“f(x)的定义域在0到正无穷大”！因为函数‘单调区间’的概念并不等于‘定义域’的概念！况且，题目核心部分还有个不等式‘ (f(x)-f(-x))/x＜0’，这就是题目给我们的一条非常重要的线索：函数f(x)的定义域内存在“互为相反的数(x和-x)”！而题设函数f(x)的单调递增区间[0, +∞)上任何俩实数都不可能形成一对“互为相反的数(即x和-x)”！因此，毫无疑问地，这题设函数f(x)的定义域并不是仅限于题设函数f(x)的单调递增区间[0, +∞)，当然更不是仅限于半开区间(0, +∞)！

　　刘志斌在题目核心部分有不等式‘(f(x)-f(-x))/x＜0’的前提下，还坚称函数f(x)的“定义域”的完全信息是题目给定的“在0到正无穷大”，刘志斌这才是‘睁着眼说瞎话’！

 　　刘志斌睁着眼说瞎话：“函数f(x)的‘定义域’的完全信息是题目给定的‘在0到正无穷大’”这刘志斌的瞎话才是地地道道的“胡说八道”！！

　　题设‘f(x)在0到正无穷大是增函数’仅仅是描述函数在半开区间[0，+∞)上有单调递增的性质而已，况且，“在0到正无穷大”并不是开区间(0，+∞)！ x轴上的开区间(0，+∞)的另一种表示为 　“ {x│x>0 }　”，而对应的“在0到正无穷大”则应表示为“{x│x≥0} ”，即题设函数f(x)在x=0处有定义！

　　刘志斌瞎咧咧：“4、那么对数函数lgx就是满足题意‘f(x)在0到正无穷大是增函数,f(1)=0’的一个函数”。这刘志斌的瞎咧咧才是地地道道的“胡说八道”！  

　　难道刘志斌不知道：对数记号‘lgx’并不是函数记号！  

　　难道刘志斌不知道：对数函数y=lgx 在x=0处没有定义！  

　　难道刘志斌不知道：负数和0都没有对数！  

　　对于<研讨会宣传员-3259>所给的这个题目，解题的人只能根据题目所给的线索（1、f(x)在0到正无穷大是增函数，2、f(1)=0，3、f(x)的定义域上有使不等式 (f(x)-f(-x))/x＜0时x的范围）来展开解题思路，去寻找符合题意的函数！  

　　刘志斌不懂这个规矩吗？刘志斌忘了自己是解题者，而不是出题者！不能由你刘志斌随意的对题意进行篡改的！  

　　原本的题意中，f(x)在实数“0”处有定义，刘志斌将其篡改为f(x)在实数“0”处没有定义；  

　　原本的题意中，f(x)定义域内有互为相反的数(x和-x)，刘志斌将其篡改为f(x)定义域内无互为相反的数；  

 　　原本的题意中，f(x)值域内有x和-x分别对应的‘函数值f(x)’和‘函数值f(-x)’，刘志斌将其篡改为f(x)值域内无‘函数值f(-x)’。  

　　刘志斌总误以为自己的‘理解’就是‘准绳’！刘志斌把题目所设函数f(x)误解为‘对数函数’然后就肆意的去篡改题目原本的意涵，让题目变为服从于刘志斌自己荒谬的‘误解’的表述形式！

　　刘志斌对题目中‘f(x)在0到正无穷大是增函数’’这一句子将‘在0到正无穷大’(即,在[0，+∞)右半开区间的意思)  篡改为‘在(0，+∞)开区间’的意思 ；

　　原本‘f(x)在0到正无穷大是增函数’是一个完整的、不可分割的“单句”，它陈述题设函数f(x)在右半开区间[0，+∞)上有单调递增的性质。刘志斌为了令题目服从于他自己的‘误解’，就肆意地把这一“单句”硬生生的拆分成两段：1) f(x)在0到正无穷大；2) 增函数， 

　　在第18楼，刘志斌曾是这样篡改的：1) 定义域是(0,+∞)；2)  是一个增函数；

　　在第72楼，刘志斌又是这样篡改的：1) “在0到正无穷大”定义区间上， 2) “增函数”， 

　　刘志斌把‘f(x)在0到正无穷大是增函数’这样一个不可分割开来的一个陈述单句，硬生生地拆分成：“1) f(x)在0到正无穷大；2) 是增函数”这两段，使之变成利于刘志斌之‘误解’的两个条件句！

　　刘志斌忘了自己是解题者，而不是出题者，解题者只能根据题设条件解题，而不能肆意篡改原题设的意涵，令题设来服从于刘志斌自己的‘误解’，从而变异成与原题设意涵不同的‘新条件’！

　　对数函数的定义域(0，+∞)并不百分百的符合题目陈述的函数f(x)‘在0到正无穷大’这右半开区间[0，+∞)上‘单调递增’的这一条件！

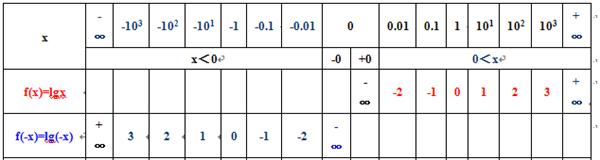
　　大家都知道，对数函数在实数“0”处没有定义！即对数函数f(x)=logax  (a＞1)的曲线向下无限延伸、向左无限靠近y轴，其横坐标“x”也永远无法到达实数“0” 处！刘志斌怎么办呢？刘志斌异想天开的把实数“0”分裂成‘两个数：-0和+0’ !　以为这样就可以达到将对数函数定义域蒙混为符合“在0到正无穷大”：[0，+∞）的目的！刘志斌这样的胡搅，实在是个大笑话！

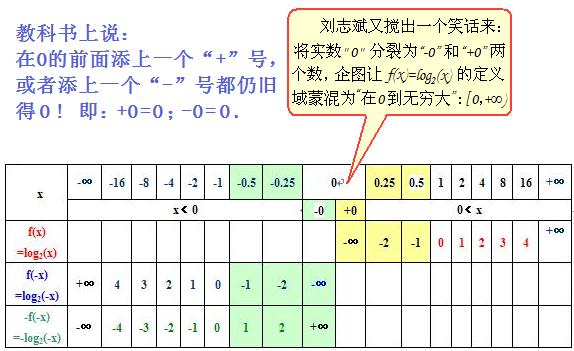
　　上面这张表格是刘志斌多次重复过的“函数表格”其中自变量数值“0”被刘志斌分裂为“-0”和“+0”！

　　看看这教科书上是怎么说的：在一个数前面添上一个“-”号，就成为原数的相反数；在一个数前面添上一个“+”号，跟原数没有区别。

　　在0的前面添上一个“+”号或者添上一个“-”号，仍旧得0，就是  +0=0 ，-0=0 。

wanggq的看法基本正确，只有一点，我首先指出题目的不完备。如果只限于题目的条件，题目是无解的！如果补充某些条件使题目可解。那么就不是原题了，所有看法我已经表白！不再一一论述！

　　寒湘子(即<烟雨朦朦>)也曾说过：实际上我们可以证明，如果函数是f(x)=x^n-1，n是正整数（显然符合题目全部条件），问题无解！ 

　　例如，f(x)=x-1，(f(x)-f(-x))/x=2>0； f(x)=x^2-1，(f(x)-f(-x))/x=0 等等，没有满足(f(x)-f(-x))/x<0的x值！

　　其实，函数f(x)=x^n-1  (n是正整数)，只能说是显然符合题设条件“f(x)在0到正无穷大是增函数，f(1)=0”，还不能说“显然符合题目全部条件”！

　　我们将寒湘子这“符合题目全部条件”的结论暂且搁置一边，先肯定寒湘子所例举的函数f(x)=x^n-1  (n是正整数)，显然符合题设条件“f(x)在0到正无穷大是增函数，f(1)=0”，且没有对题目补充某些条件！寒湘子该不会否认吧？ 

　　f(x)=x^n-1  (n是正整数) 这样的函数，其定义域是(-∞，+∞)。在刘志斌的意识里，用这样的函数来解这个题目，就是“给原题目已知函数f(x)补充了0到负无穷大区间”！其实，这正是刘志斌缺乏正确的函数基础知识的表现！

　　寒湘子和刘志斌不一样，刘志斌弄不懂“单调区间”与“定义域”这两个不同概念之间的联系和区别，而寒湘子是懂的！

　　所以，寒湘子和我们一样，不会把题设函数f(x)误解为定义域仅限于原点右边一侧的函数f(x) 。寒湘子所举的例子f(x)=x-1 和 f(x)=x^2-1  都符合“f(x)在0到正无穷大是增函数，f(1)=0”  。但是，寒湘子例举的这两个函数却都没有满足题目：“所设f(x)上有(f(x)-f(-c))/x<0时”！

　　寒湘子下结论说“如果只限于题目的条件，题目是无解的！如果补充某些条件使题目可解。那么就不是原题了”

　　那么，如果没有对原题目补充某些条件，题目当真就无解吗？大家看了下述的一例函数就会明白：不对原题目补充任何条件，该题目也是会有解的！

　　对照寒湘子所举的例子f(x)=x-1 和 f(x)=x^2-1 ，现在老王也例举一个定义域为(-∞，+∞)的函数：f(x)=3x^4-8x^3+6x^2-1  寒湘子该不会误认为此例函数给原题目“补充了某些条件”吧！

　　我们可以证明，f(x)=3x^4-8x^3+6x^2-1　第一，在0到正无穷大是增函数，第二，f(1)=0，　第三，自变量x在除0 之外的实数范围内都能满足(f(x)-f(-x))/x＜0 。即：当函数是f(x)=3x^4-8x^3+6x^2-1时，题目是有解的！

　　此解为：(f(x)-f(-x))/x＜0时x的范围是 {x│x∈R，且x≠0}

　　寒湘子所谓的“如果函数是f(x)=x^n-1 （n是正整数）显然符合题目全部条件”是对题目“全部条件”的误解！因为题设的两个条件“f(x)在0到正无穷大，”和“f(1)=0 ，”并不是题目“全部”的条件。

　　寒湘子在审题时忽视了题目的核心内容“求(f(x)-f(-x))/x<0时x的范围”。这核心内容分明蕴涵着题目的第3个条件：“题目所设f(x)有(f(x)-f(-x))/x<0时”！

　　寒湘子的例1： f(x)=x-1，(f(x)-f(-x))/x=2>0 ，即：f(x)=x-1上没有(f(x)-f(-x))/x<0时；

　　寒湘子的例2： f(x)=x^2-1，(f(x)-f(-x))/x=0 ，即：f(x)=X^2-1上没有(f(x)-f(-x))/x<0时；

　　一般地，f(x)=x^n-1 （n是正整数） 当n是奇数时，(f(x)-f(-x))/x=2x^(n-1) >0；当n是偶数时，(f(x)-f(-x))/x=0。不论n是奇或是偶，都没有满足题目“所设f(x)上有(f(x)-f(-x))/x<0时”这个“重要条件”！

　　请注意：函数曲线上有“(f(x)-f(-x))/x<0 时”也算是这个题目的一个‘条件’！而且这个‘条件’就蕴含在题目核心内容“求(f(x)-f(-x))/x<0时x的范围”之中！

引用 wanggq 的回复内容： 　　根据原题目“题设”中的条件： 　　1)、f(x)在...

没错，支持下！

　　题目所给出的条件，除了有：

　　1)、“f(x)在0到正无穷大是增函数,”

　　 2)、“f(1)=0,” 

　　之外，还有第三个条件！这第三个条件就蕴涵在题目的核心内容之中！

　　这题目核心部分“求(f(x)-f(-x))/x＜0 时 x的范围”中所蕴含的条件是：

　　3)、所设函数f(x)的自变量在定义域内有满足使(f(x)-f(-x))/x＜0时 的范围。

　　（这蕴含在题目核心部分“求(f(x)-f(-x))/x＜0 时 x的范围”中的第3个条件可不是老王自己添加的，而是老王用慧眼从原题目的字里行间看出来的！）

　　即便原题目有上述的3个条件，但这3个条件也不能完全确定出原题目之函数f(x)具体的映射法则！

　　但是，刘志斌却振振有词的胡扯什么：“1、f(x)在0到正无穷大；2、是增函数；3、函数过（1，0）点。原题目明显就是说的对数函数！”

　　题目中的“f(x)在0到正无穷大是增函数”是一个完整的、不可分割的“单句”！它只表示1个意思：“f(x)在右半开区间[0,+∞)上有单调递增的性质”即第1个条件。

　　刘志斌故意的把题目的第1个条件硬生生的拆分为“1、f(x)在0到正无穷大；2、是增函数；”两段，形成两个条件！

　　再把原题目的第2个条件“f(1)=0，即：f(x)过(1，0)点”冒充为“第3个条件”！

　　从而将原题目真正的第3个条件“f(x)的定义域上有使(f(x)-f(-x))/x＜0时的范围”给隐匿起来！这说明刘志斌在恶意的篡改题目！

　　题目一经篡改，刘志斌就可以堂而皇之的谎称：“原题目明显就是说的对数函数”！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

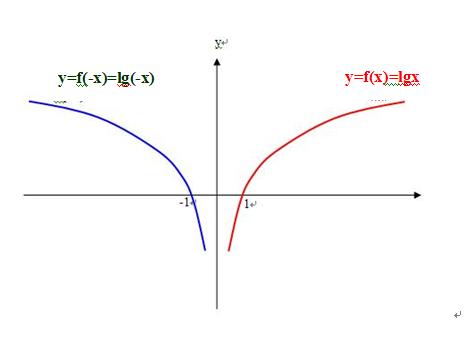
　　请看，刘志斌荒谬的对同一个对数函数f(x)=logax胡搅出多条曲线来：

 　　刘志斌在他的曲线图(同一个坐标系)上：

　　y轴右侧的曲线上标注的是“f(x)=logax” ,其定义域是x＞0 即定义域是开区间(0,+∞)，自变量在这个区间上不可能取得互为相反的数值，所以无从谈起f(-x)！

　　正如烟雨朦朦对“单边型定义域”这类函数指出的：对于x＞0，f(-x)没有定义；对于x＜0，f(x)也是没有定义的 !


　　刘志斌对y轴左侧的曲线上标注的是“f(-x)=loga(-x)” ，这就是刘志斌犯的一个错误！

　　在同一个曲线图中讨论函数时，相同的记号“f( )”只表示同一个“函数对应法则”！ 既然刘志斌在右侧曲线上已经标注了f(x)=logax，而f(x)=logax是不存在“f(-x)”的！刘志斌又怎么胆敢指鹿为马地给y轴左侧的曲线标上“f(-x)”呢 ? ! 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　正确的做法应该是：用另一个字母来作y轴左侧曲线的“函数对应法则”的记号，如“h( )” 以示区别于右侧曲线的“f( )”！因为它们本来就是两个不同“对应法则”的函数：

　　f(x)=logax，函数的对应法则为：“因变量y是自变量x的对数”，定义域为x＞0 .

　　h(x)=loga(-x)，函数的对应法则为：“因变量y是自变量x相反数的对数”，定义域为x＜0 .

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　其实，这个h(x)已经不是自变量x的对数了，它只是一个“中间变量”的对数！要把这个问题弄清楚，就应该温习一下“复合函数”的概念：

　　如果y是u的函数：y=g(u). 而u又是x的函数：u=ρ(x)　且ρ(x)的值域使g(u)有定义，那么，y通过u的联系也是x的函数：y=h(x) . 我们就称y=h(x)是由函数g(u)及ρ(x)复合而成的函数，简称复合函数.记作y=g[ρ(x)]，其中的u 叫做“中间变量”.
　　
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　现在有：y=g(u)=logau，函数的对应法则为,“因变量y是自变量u的对数",定义域为u＞0 .

　　而函数u=ρ(x)=-x   函数的对应法则为:“因变量u是自变量x的相反数”,定义域限为x＜0 ，

　　由函数g(u)及ρ(x) 复合而成的函数h(x)=g[ρ(x)]=loga(-x)，同样也不存在“h(-x)”！因为自变量在定义域(x＜0)上也不可能取得互为相反的数值！也就无从谈起“h(-x)”！

　　刘志斌把题目所涉函数f(x)定义域曲解为开区间(0，+∞)，并断言该函数f(x)就是对数函数logax (a＞1)才是“多么可笑的”曲解！“多么可笑的”断言！ 

　　刘志斌却反过来胡批老王的正确见解是“多么可笑的一段话”，下面是截屏证据：

　　题目之题设“f(x)在0到正无穷大是增函数，”并不是描述函数的定义域！况且，这句“在0到正无穷大”表达的是右半开区间[0,+∞)，与开区间(0,+∞)还是有点儿区别的！

　　函数是增函数还是减函数，是对定义域内某个区间而言的。

　　函数y=x^2 “在0到正无穷大是增函数”，难道刘志斌也可以曲解为函数y=x^2 的定义域是“在0到正无穷大”右半开区间？！难道刘志斌也可以曲解为函数y=x^2 的定义域是开区间(0，+∞) ？！

　　刘志斌曲解题设的函数f(x)定义域为(0，+∞) 才是“多么可笑的”曲解！！

　　所以，不能象刘志斌那样，单凭题目中提及函数“在0到正无穷大是增函数”，就荒谬的把函数的定义域判定为“在0到正无穷大”！更不能象刘志斌那样把函数的定义域曲解为开区间(0，+∞) ！

　　如果题目所指的函数f(x)的定义域真的是“在0到正无穷大”，或如刘志斌所曲解的开区间(0，+∞)，那么，题目的核心内容“求(f(x)-f(-x))/x＜0时x的范围”就毫无意义！

　　因为这不等式里的“f(x)”与“f(-x)”分别是自变量在函数f(x)定义域内的两个互为相反的数的值“x”与“-x”对应的俩“函数值”!　而“在0到正无穷大”右半开区间内，或(0，+∞)开区间内都绝无可能存在有与“x”相反的数“-x”!

　　正因为题目中有核心内容“求(f(x)-f(-x))/x＜0时x的范围”存在，所以，题目所设的函数f(x)的定义域必定延伸到x＜0的区域！

　　老王可以举出很多完全符合题目之题设：“f(x)在0到正无穷大是增函数，

f(1)=0　”，且符合“有使(f(x)-f(-x))/x ＜0时x的范围”的函数例子： 

　　譬如，分段函数f(x)=f1(x)=x^2-0.5  (当x＜0)；f(x)=f2(x)=0.5x^2-0.5  (当x≥0).

　　又譬如，函数f(x)=3x^4-8x^3+6x^2-1 .

　　再譬如，函数f(x)=x-ln[(1+x)/2]-1 .　

　　……等等！

　　老王所举的这些函数例子，每一个函数f(x)都能完全符合题设“f(x)在0到正无穷大是增函数，f(1)=0 ”，并且符合“有使(f(x)-f(-x))/x＜0时x的范围”！

　　刘志斌自认为有“本事”来否定“符合题设f(x)在0到正无穷大是增函数，f(1)=0，并且有使(f(x)-f(-x))/x＜0时x的范围的函数f(x)有很多”！那么，刘志斌怎么不敢晒出你的“本事”来“证”出老王所举各例函数不符合题设，或没有(f(x)-f(-x))/x＜0时x的范围（哪怕你仅仅是只“证”出1例不符合题设，或没有(f(x)-f(-x))/x＜0时x的范围）？！

　　刘志斌拿不出任何“真凭实据”来否定老王所举诸例函数f(x)其中之任何1例，只在那里无根无据的乱喊乱叫个啥子“多么可笑的一段话”。这只能说明刘志斌对函数基本概念的无知！

　　相反，刘志斌所举的“对数函数f(x)=logax”在x=0处无定义，所以，刘志斌例举的这个对数函数虽然符合f(1)=0，但它并不真正符合题设的“f(x)在0到正无穷大是增函数”！在单调递增性这方面，它仅只为“在大于0到正无穷大是增函数”。

　　而且，刘志斌胡搅的对称于y轴的图形根本就不可能有“让(f(x)-f(-x))/x＜0时x的范围”！所以，刘志斌的曲解才是“多么可笑的”一个谬误解！

这个题目只是讨论实变函数。在实变函数范围，负数的对数函数是没有意义的。但是在复变函数里，负数的对数函数是有意义的，但是复数一般的讲，就不能和0论大小！除非复数刚好落在实数轴上。你不能讲i>0而-i<0。这里i是-1的平方根！至于刘老师的原话我没有去查，不对楼主本身的话做评论。根据题目既然一个表达式要小于0，它就不可能是非实复数。

　　　<研讨会宣传员-3259>的这篇帖子叫什么来着？叫《昨天一道高中的数学题……》！在高中数学里研究的函数叫“一元实函数”简称函数！寒湘子就别扯到“复函数”去了！

　　看看刘志斌胡搅的这个“对数函数y=f(-x)=lg(-x)”公然的与正统理论中的对数函数y=f(x)=lgx 相抵触：

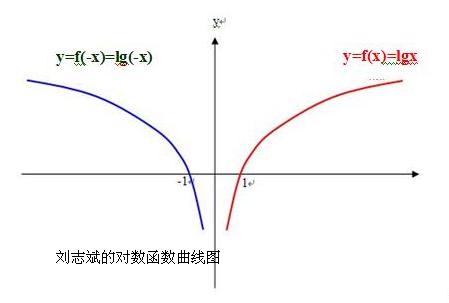
　　在正统理论里，零和负数没有对数！所以，对数函数的定义域是开区间(0，

+∞),对数函数的曲线完全不可能跑到平面直角坐标系的第2、3象限去！

　　下面是教科书上的对数函数的图象：

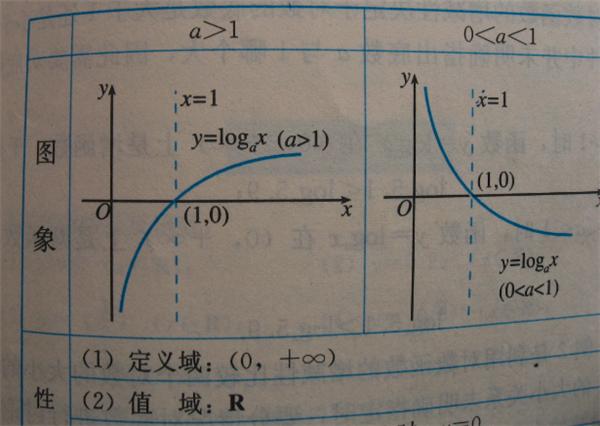
　　符号“y=f(x)”表示“y是x的函数”，符号“y=f(x)=lgx”表示“y是以10为底，x的对数函数”，在对数函数的定义域(0，+∞)内绝无x的相反数“-x”的存在！所以，也就绝无对数函数值“f(-x)”即绝无“f(-x)=lg(-x)”的存在！

引用 寒湘子 的回复内容： 

       这个题目只是讨论实变函数。在实变函数范围，负数的对数函数是没有意义的。……

1、wanggq说“正统科学体系中，学者们都一致信守“负数没有对数”的理念，刘志斌却认为那是他们钻牛角尖！不懂函数图象的翻转和移动！而我刘志斌“刘大师”非常有能耐，学者不能的，我刘志斌“刘大师”却能，所以“刘大师”就开天辟地创立了新的“对数函数loga(-x)”!”；

2、wanggq认为对数函数“loga(-x) ”的-x是“负数”，负数没有对数，所以wanggq认为是开天辟地创立了新的“对数函数loga(-x)”!”；

3、寒湘子应声附和，“在实变函数范围，负数的对数函数是没有意义的。……”；

4、按照wanggq的观点，x是正数，loga(x) 一定有意义， 寒湘子你说是吧？？？

5、寒湘子请回答，loga(x)一定有意义，loga(-x)一定无意义，是这样吗？

6、我把wanggq和寒湘子好有一比，就像两个把自己耳朵掩住，心里想这下谁也听不见，大着胆子盗铃的“伙伴”一样！

7、我们在学对数函数时，loga(x) 的图像在1、4象限，因为它的x只能是正数；

8、我把对数函数loga(-x) 的图像画在2、3象限，因为它的-x只能是正数；

9、wanggq看不懂，乱喊叫可以理解，寒湘子应声附和也不懂吗？？？

10、看看下图，哪个是负数的对数？-x是负数吗？