昨天一道高中的数学题,我竟然不会做了 点击:23739 | 回复:1402
楼主最近还看过
在学术界都认为:关于y轴对称的函数,在x≠0时,其“f(x)-f(-x)”的值是绝不可能与自变量的值x异号的!
但是,刘志斌“牛”得很!他自认为“学术界所不能的事情,我‘牛大师’却能!把概念搅一搅,不就能啦?!”
刘志斌假借把“f(x)-f(-x)”看作“f(-x)”与“-f(-x)”的代数和:
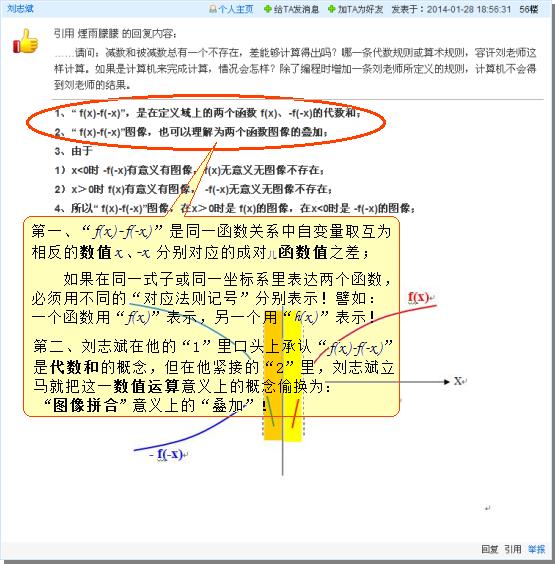
刘志斌口头上承认表达式f(x)-f(-x)是‘代数和’,但是,刘志斌在实际的运算操作上却并不遵循代数运算的规则!恶意的将‘代数和’这一数值运算意义上的概念偷换为“图象拼合”意义上的“叠加”!
在同一表达式或同一坐标系里, f(x)、f(-x) 是同一函数关系中自变量取互为相反的数值x、-x分别对应的成对儿函数值。
所以,“f(x)-f(-x)”是同一函数关系中自变量取互为相反的数值x、-x分别对应的成对儿函数值之差!
刘志斌却打胡乱说:“1、“ f(x)-f(-x)”,是在定义域上的两个函数 f(x)、-f(-x)的代数和”
如果你是在同一表达式或同一坐标系里表达“不同对应法则”的两个函数,那么你就必须用不同的“对应法则记号”分别表示!譬如:一个函数用f(x)表示,另一个函数用h(x)表示,以区别于f(x) !
同一函数中成对儿函数值之间的运算是在同一定义域中进行的运算,所以题目中“f(x)-f(-x)”的运算是有意义的运算。
而两个函数之间的运算,必须是限制在两个函数的公共定义域上的运算才是有意义的运算!否则,其运算是无意义的、不能成立的!
刘志斌把题目所指的同一函数关系中,自变量取互为相反的数值x、-x分别对应的成对儿函数值f(x)、f(-x)误读为“两个不同对应法则的函数”。
并且,刘志斌分别赋予他所谓的“两个函数”相互没有交集的定义域。即“两个函数”没有公共定义域!那么这“两个函数”就没有相互运算的意义!
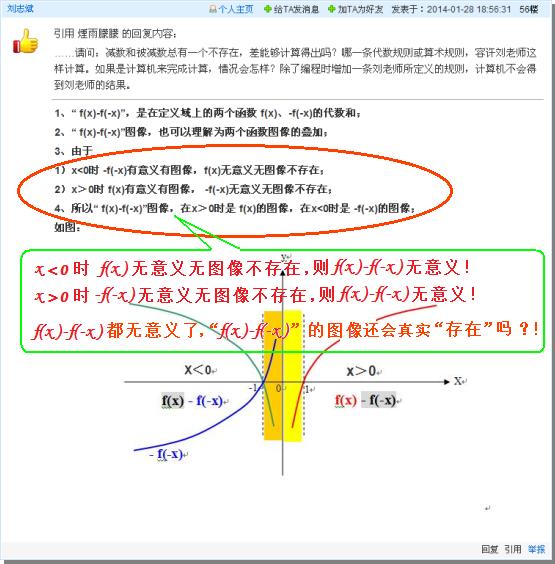
<烟雨朦朦>质疑刘志斌的没有公共定义域的“两个函数”的运算“减数和被减数总有一个不存在,差能够计算得出来吗?” 刘志斌针对该质疑的回复,纯粹是偷换概念的胡搅乱弹:『1、‘f(x)-f(-x)’是在定义域上的两个函数 f(x)、-f(-x)的代数和;2、“ f(x)-f(-x)”图像,也可以理解为两个函数图像的叠加;3、由于1)x<0时 -f(-x)有意义有图像,f(x)无意义无图像不存在;2)x>0时 f(x)有意义有图像, -f(-x)无意义无图像不存在;4、所以“ f(x)-f(-x)”图像,在x>0时是 f(x)的图像,在x<0时是 -f(-x)的图像;』
即便你刘志斌把“f(x)-f(-x)”看成“f(x)+[-f(-x)]”,你刘志斌同样不能回避“参与运算的两个两个‘数’之中任何一个‘数’无意义或曰不存在时,该‘运算’是否还有意义?”的问题!
举例说,0是不能作除数的!譬如‘2’除以‘0’ 即‘2/0’ 是无意义的。根据除法是乘法的逆运算,我们可以将‘2/0’看成是“与0相乘,其积为‘2’的数 ” 因为任何一个数与0相乘,其积都不可能为‘2’ , 所以‘2/0’ 这个“数”是不存在的!
那末,当减数无意义、不存在之时,如运算:3-(2/0) 是无意义的!看成代数和运算: 3+(-(2/0)) 也是无意义的!
当被减数无意义、不存在之时,如运算:(2/0)-5 是无意义的!看成代数和运算:(2/0)+(-5) 也是无意义的!
同理,“1)、x<0时 ,f(x)无意义无图像不存在”那末,运算“f(x)-f(-x)”就失去意义!
“2)、x>0时, -f(-x)无意义无图像不存在”那末,运算“f(x)-f(-x)”也失去意义!
没有意义的运算“f(x)-f(-x)”是没有结果的!既然没有结果,那就没有对应的图像!
刘志斌却打胡乱说:『x<0时 -f(-x)有意义有图像,f(x)无意义无图像不存在,所以“ f(x)-f(-x)”图像是 -f(-x)的图像;x>0时 f(x)有意义有图像, -f(-x)无意义无图像不存在,所以“f(x)-f(-x)”图像是f(x)的图像”』
难道在刘志斌的意识里,失去意义的运算还会得出“运算结果”?并还会由这个根本不存在的所谓的“结果”而得到其“图像”?!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
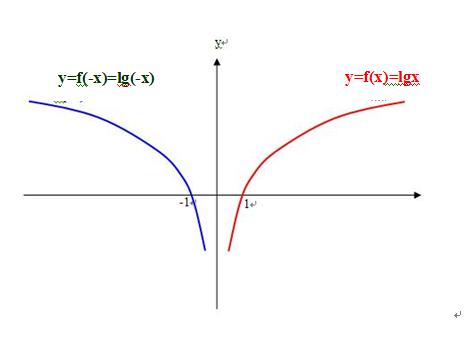
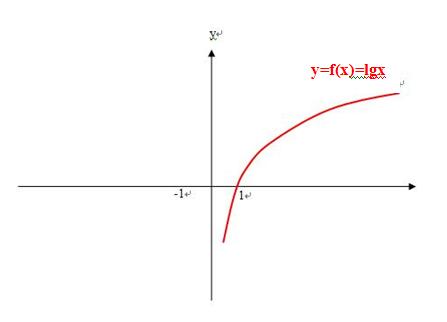
刘志斌曾经竭尽挖苦诋毁之能事,踏削<烟雨朦朦>不了解对数函数知识、想不到“f(x)=logax”, 而是想到一些:f(x)=lxl-1 、f(x)=x-1 、f(x)=x^2-1、 f(x)=x^3-1、……
其实,是刘志斌自己不了解函数的基础知识,才荒谬的以为“符合f(x)在0到正无穷大是增函数,f(1)=0 条件的函数只有对数函数”!
他刘志斌并不知道:“符合f(x)在0到正无穷大是增函数,f(1)=0 条件的函数f(x)事实上是数不胜数的!”并不如他刘志斌所乱说‘是唯一的’!
刘志斌与<烟雨朦朦>激烈争论达80个帖子,才认识到他刘志斌曾经竭尽挖苦诋毁之能事踏削的<烟雨朦朦>所举函数例子,其实都是符合“f(x)在0到正无穷大是增函数,f(1)=0 ”条件的!
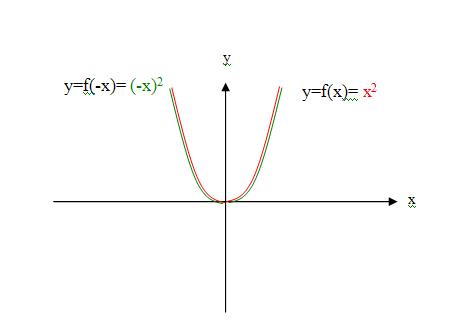
于是,刘志斌为了弥补他第一个答案所存在的“f(x)、f(-x)总有一个无意义,以及f(0)无意义”的弊病,因而抄袭了<烟雨朦朦>所举的例子f(x)=lxl-1来作为他第二个答案中,解题用的函数f(x). 如右下图的曲线所示:
懂得函数定义的同学们都能看出来:上面左图曲线与右图(除去“-f(-x)”之外的)曲线各自表达的“映射关系”完全是同一个“映射”!
图象直观的告诉我们:f(x)= IxI-1 不折不扣的符合“f(x)在0到正无穷大是增函数,
f(1)=0” !
需要加以说明如下几点:
1、<烟雨朦朦>举出诸多符合题设“f(x)在0到正无穷大是增函数,f(1)=0 ”的函数例“ f(x)=IxI-1 、f(x)=x-1 、f(x)=x^2-1、 f(x)=x^3-1、……”目的是要表达:不折不扣符合“f(x)在0到正无穷大是增函数,f(1)=0” 条件的函数f(x)并不是如刘志斌所乱说‘唯一只有对数函数’,而事实上是数不胜数的!且刘志斌举的函数f(x)=logaX只能算是打了折扣的、擦边球式的“符合条件”!
2、虽然符合“f(x)在0到正无穷大是增函数,f(1)=0”条件的函数f(x)数不胜数,但是,在它们之中,不符合“有使(f(x)-f(-x))/x<0时x的范围”的函数f(x)也是数不胜数的!
3、例如: f(x)=IxI-1曲线是关于y轴成对称的图形,但凡关于y轴成对称图形的函数f(x),其f(x)-f(-x)≡0 ,故不符合“有使(f(x)-f(-x))/x<0时x的范围”!
4、<烟雨朦朦>所举出的诸多函数例中,没有提到‘对数函数f(x)=logaX ’ 并不是<烟雨朦朦>想不到对数函数f(x)=logaX ,而是<烟雨朦朦>坚决的否定f(x)=logaX 用来解答本题目的“可能性”!因为‘单边型定义域’的函数f(x)使表达式f(x)-f(-x)完全没有意义!刘志斌用‘对数函数f(x)=logaX ’来解答本题目,从根本上就已经犯错啦!
5、刘志斌做第二个答案时,抄袭仿照烟雨朦朦的“f(x)=IxI-1”曲线原本是能使得表达式f(x)-f(-x)有意义的,但由于刘志斌的胡搅,又让刘志斌给搅得荒谬和糟糕透了!
函数“f(x)=IxI-1”定义域是 { x│x∈R },在“f(x)=IxI-1”定义域内任意某取值x 其相反数‘-x’也都在该定义域内。所以,对于整个定义域,f(x)-f(-x)都是有意义的!
例如设: x=2 , 有 f(x)=f(2)=│2│-1=1 则:-x=-2 , 有 f(-x)=f(-2)=│-2│-1=1
∴ f(2)-f(-2)=0 即:f(x)-f(-x)=0
函数“f(x)=IxI-1”的自变量x也可以取任何的某一负数
例如设: x=-2 , 有 f(x)=f(-2)=│-2│-1=1 则:-x=2 , 有 f(-x)=f(2)=│2│-1=1
∴ f(-2)-f(2)=0 即:f(x)-f(-x)=0
但是,刘志斌主张的乱弹理论是怎样运算这个例子的呢?刘志斌的运算逻辑是这么荒谬透顶的:
『 设函数f(x)在(0,+∞)上是增函数,f(1)=0 则 g(x)=f(x)-f(-x),x>0时 g(x)=f(x),x<0时 g(x)=-f(-x)』
设 x=2 时, 有 f(x)=f(2)=│2│-1=1 ;f(-x)=f(-2)=│-2│-1=1
若按“刘志斌理论”的逻辑来运算:x>0时 g(x)=f(x) 即 f(x)-f(-x)=f(x)
f(x)-f(-x)=f(2)-f(-2)=1-1=f(x)=f(2)=1 这按刘志斌的运算逻辑来运算出的结果明显是混账结果!
设 x=-2 时, 有 f(x)=f(-2)=│-2│-1=1 ;f(-x)=f(2)=│2│-1=1
若按“刘志斌理论”的逻辑来运算:x<0时 g(x)=-f(-x) 即 f(x)-f(-x)=-f(-x)
f(x)-f(-x)=f(-2)-f(2)=1-1=-f(-x)=-f(2)=-1 这按刘志斌的运算逻辑来运算出的结果明显是混账结果!
众所周知:但凡关于y轴成对称图形的函数曲线,因为f(-x)≡f(x),所以,当x≠0 的情形下,(f(x)-f(-x))/x≡0 !
只要把这一众所周知的结论跟刘志斌的先后俩答案比照一下,便清楚的显现出刘志斌胡搅的俩答案都是错误的!!
刘志斌的曲线图上多出一条所谓的“-f(-x)”曲线又是什么会事呢?把f(x)-f(-x)看成代数和,就能够改变函数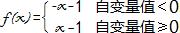 使题目核心的不等式(f(x)-f(-x))/x<0 不能获得成立的事实吗?根本就是不可能改变的!
使题目核心的不等式(f(x)-f(-x))/x<0 不能获得成立的事实吗?根本就是不可能改变的!
对于偶函数f(x),有:f(x)-f(-x)≡0 . “f(x)-f(-x)” 的图像是重合于x轴的一条直线。很明显,在x≠0 时,“f(x)-f(-x)”的值“0”,绝不可能与x异号!即:偶函数绝不可能使(f(x)-f(-x))/x<0 有获得成立的x的范围!
大家都知道:“减去一个数,等于加上这个减数的相反数”!
举例说:5减去3等于2 . 即 5-3=2 , 我们可以把5-3看作“5”加上“-3” !即 “5”与“-3”的代数和:5+(-3),其代数和仍然等于2 , 也仍然写作“5-3=2” !
这是根据“代数运算”去括号的法则:括号前是“+”号的,该“+”号连同括号一起去掉时,括号内各项不变号。如:5+(-3)=5-3=2
再举例说:3减去3等于0 . 即 3-3=0 , 我们可以把3-3看作“3”加上“-3” !即 “3”与“-3”的代数和,其代数和仍然等于0 , 仍然写作“3-3=0 ” !
可见,把一个减法表达式看成“代数和”表达式,其运算结果与原减法表达式运算结果是相同的!绝无可能变成另一种结果!这是因为“减法运算”与“代数和运算”同属于“代数运算”的范畴,同属于数值概念意义上的运算!
刘志斌却妄图假借把“f(x)-f(-x)”看作“f(-x)”与“-f(-x)”的代数和,就能让“f(x)-f(-x)”变成另一种结果!事实证明刘志斌的胡搅是一种无知的表现!
5、函数图像在坐标系中的位置变换包括平移、翻转、旋转,函数图像的形状变化包括伸缩;
1)平移
水平平移:设函数f(x),则函数f(x+a)的图像为已知函数f(x)的图像向左(a>0)移动a各单位;
竖直平移:设函数f(x),则函数f(x)+a的图像为已知函数f(x)的图像向上(a>0)移动a各单位;
2)翻转
水平翻转:设函数f(x),则函数f(-x)的图像为已知函数f(x)以y轴翻转180°所得图像;
垂直翻转:设函数f(x),则函数-f(x)的图像为已知函数f(x)以x轴翻转180°所得图像;
3)旋转
任意角旋转
90°角旋转:设函数y=f(x),则函数x=f(-y)的图像为已知函数f(x)以原点为转轴逆时针旋转90°所得图像;
180都角旋转:设函数f(x),则函数-f(-x)的图像为已知函数f(x)以坐标原点为轴旋转180°所得图像;
4)伸缩
水平伸缩:设已知函数f(x),则函数f(ax)(a>0)的图像为已知函数f(x)的图像沿水平方向压缩a倍;
竖直伸缩:设已知函数f(x),则函数af(x)(a>0)的图像为已知函数f(x)的图像沿竖直方向扩大a倍;
6、下来看看主楼题目属于那种情况:
1)原题“f(x)在0到正无穷大是增函数,f(1)=0,求(f(x)-f(-x))/x<0时x的范围”;
2)已知函数“f(x)在0到正无穷大是增函数,f(1)=0,”;
3)求解“求(f(x)-f(-x))/x<0时x的范围”;
4)所以已知函数f(x)的定义域为x>0,图像在2、4象限,单调递增函数,与x轴有一交点f(1)=0;求解函数为f(-x)、-f(-x),所以此题目属于已知函数f(x),求函数f(-x),属于函数变换中的水平翻转问题;
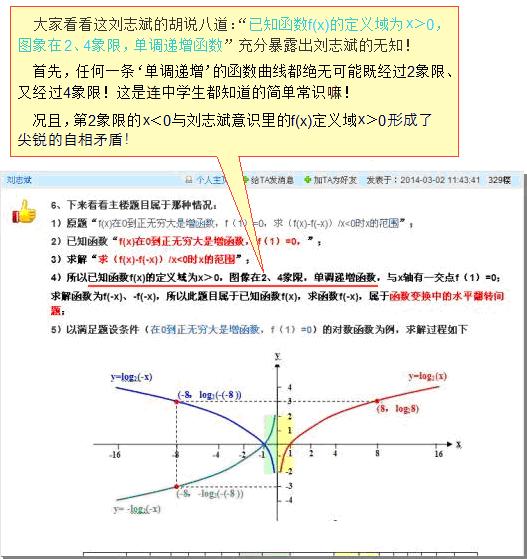
5)以满足题设条件(在0到正无穷大是增函数,f(1)=0)的对数函数为例,求解过程如下
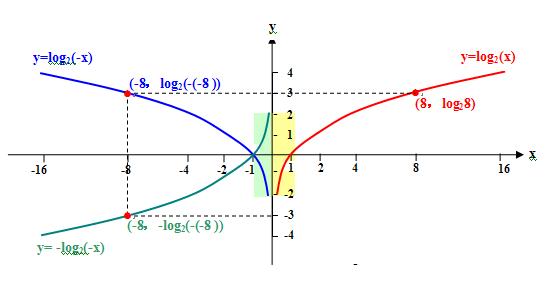
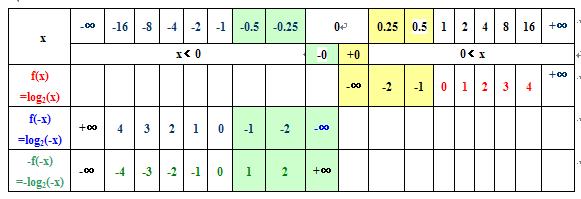
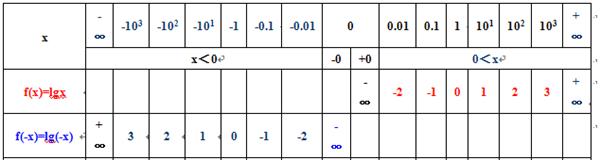
-1< x<0 f(x)-f(-x))/x = -f(-x)/x < 0 如图中绿色部分;
0 <x<1 f(x)-f(-x))/x = f(x)/x < 0 如图中黄色部分;
题目设“f(x)在0到正无穷大是增函数”意思是说函数f(x)在半开区间[0,+∞)上有单调递增的性质。并不是说函数f(x)的定义域是开区间(0,+∞)!
刘志斌把函数“单调区间”的概念误当成函数“定义域”的概念,是一个很低级的错误,是基本知识不够的表现:
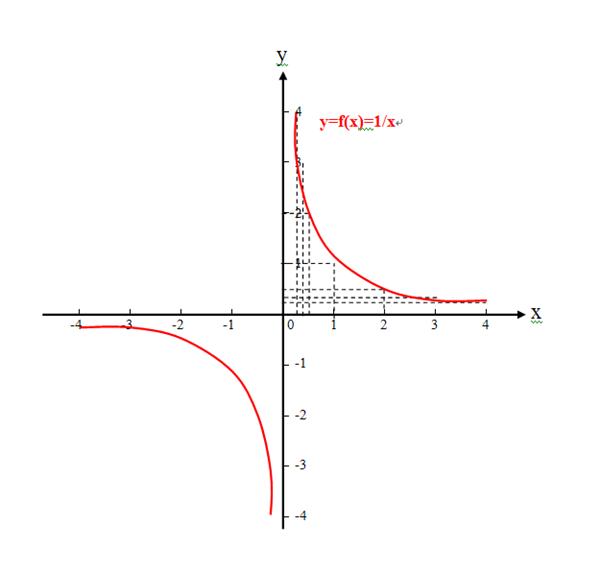
举例来说,教科书上要求学生证明函数f(x)=1/x 在(0,+∞)上是减函数,
刘志斌是否也要说:2)、已知函数f(x)=1/x 在(0,+∞)是减函数;
3)、……
4)、所以已知函数f(x)的定义域为x>0 ,
(请对照图片上绿线框内刘志斌的错误言论:2)、已知函数f(x)在0到正无穷大是增函数;……4)、所以已知函数f(x)的定义域为x>0,)
刘志斌把函数“单调区间”的概念混淆为函数“定义域”的概念是一个很低级的常识错误!
老王已经多次提醒过刘志斌了!现在再一次的提醒刘志斌,
函数的“单调区间”概念≠ “定义域”概念!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
高中的学生都知道:反比例函数f(x)=1/x 的定义域是:{ x∈R,且x≠0 }!
某个题目说f(x)=1/x在(0,+∞)是减函数,并不是表达该函数的“定义域”是
(0,+∞)!!
而仅仅只是对函数f(x)=1/x 在(0,+∞)区间上的单调性质进行一个描述而已!
同理,楼主的题目中“f(x)在0到正无穷大是增函数”也仅仅是对f(x)在[0,+∞)区间的“单调性质”进行描述而已!
刘志斌之前一直夹着屎犟:『 11、任何情况下,f(x)、f(-x)是两个函数……12、任何情况下,f(x)、f(-x)都不是一个函数……13、任何情况下,f(x)、f(-x)都不是一个函数f(x)图像上的两个函数值;』
322楼、323楼刘志斌的发言已经自己否定他自己在之前的这些胡言乱语啦!
刘志斌不敢再坚持说“任何情况下,f(x)、f(-x)是两个函数……任何情况下,f(x)、f(-x)都不是同一个函数……任何情况下,f(x)、f(-x)都不是同一个函数f(x)图像上的两个函数值;”不得不转而承认:
『1、当一个函数f(x)的定义域为(-∞, +∞)时,当自变量x取两个相反数x、-x时,对应的函数值分别为f(x)、f(-x);
…… 2)f(x)=-f(-x),f(x)、f(-x)互为相反数,……』
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
既然现在刘志斌已经承认符号f(-x)是表示函数值,那么,对于定义域为(-∞, +∞)的函数f(x), 其自变量取互为相反的数值x、-x 分别对应函数值f(x)、f(-x),现在争论的双方就已经没有争议啦!
但是,并不仅限于定义域为(-∞, +∞)的情况才有成对儿的函数值f(x)、f(-x),我们可以将认识扩展到定义域中有“关于0点对称的区间”的情况。
譬如:函数f(x)=x-ln[(1+x)/2]-1 的定义域为(-1, +∞) 。请大家注意,开区间(-1, 1) 是“关于0点对称的区间”,并且区间(-1, 1)包含于定义域(-1, +∞) 。所以,自变量在开区间(-1, 1) 内取任何互为相反的数值x、-x分别对应的成对儿函数值也表示为f(x)、f(-x) !如下图所示涂有底色背景的区间(-1,1)内对应存在成对儿函数值f(x)、f(-x):
而左闭右开区间[1,+∞),虽然也包含于该函数定义域(-1,+∞),但是,区间[1,+∞)内的任何某一取值x 其相反的数值-x,全都落在定义域之外啦!所以在区间[1,+∞)内只存在对应函数值f(x),而不存在对应函数值“f(-x)”!
对于该函数f(x)定义域(-1,+∞) 之外的左开右闭区间(-∞,-1],既不存在对应的“函数值f(x)”,也不存在对应的“函数值f(-x)” !
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
关于奇函数、偶函数的定义:
设函数f(x)的定义域X是一个对称的数集(但不一定是(-∞,+∞)),即对于任何x∈X,都有-x∈X。对于函数f(x) (x∈X):
1、如果恒有f(-x)=-f(x),则称函数f(x)为奇函数;
2、如果恒有f(-x)= f(x),则称函数f(x)为偶函数。
判断函数f(x)的奇偶性,要依据奇函数或偶函数的定义,看当x∈X时,是否恒有:f(-x)=-f(x), 或 f(-x)=f(x) 。
f(-x)=-f(x) 恒成立时,函数f(x)是奇函数;f(-x)=f(x)恒成立时,函数f(x)是偶函数。
如果一个函数是奇函数,或者是偶函数,那么这个函数的定义域一定是关于0点对称的。例如函数y=1/x是奇函数,它的定义域关于0点对称。 如果一个函数的定义域不关于0点对称,那么它不具有奇偶性。例如函数y=x^(-1/2)既不是奇函数也不是偶函数,因为它的定义域为(0,+∞),即x取负值无意义,所以它不满足奇函数的或偶函数的定义; 再例如函数f(x)=x-ln[(1+x)/2]-1既不是奇函数也不是偶函数,因为它的定义域为(-1,+∞),不是对称的数集,所以它不满足奇函数的或偶函数的定义 。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
322楼、323楼刘志斌虽然不得不承认“f(x)、f(-x) 分别为自变量取互为相反数x、-x时,分别对应的函数值”,但是,刘志斌仍然忘不了继续的胡搅:
『2、对于任意一个函数f(x),自变量当自变量x取两个相反数x、-x时,对应的函数值分别为f(x)、f(-x):
1)f(x)=f(-x),f(x)为偶函数;
2)f(x)=-f(-x),f(x)、f(-x)互为相反数,f(x)为奇函数;
3)f(x)≠f(-x),但是 f(x)、f(-x)都有意义;
4)f(x)、f(-x)不都有意义,举例说对数函数,』
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
刘志斌的『2、对于任意一个函数f(x),自变量当自变量x取两个相反数x、-x时,对应的函数值分别为f(x)、f(-x) 』把重要的前提“定义域内有互为相反的数值x、-x可取。即x、-x是同属于定义域的元素”抛开来谈“-x对应的函数值f(-x)”,为他的『f(x)=logax,f(-x)=loga(-x) 』诡辩做铺垫!
刘志斌的『1)f(x)=f(-x),f(x)为偶函数;2)f(x)=-f(-x),f(x)、f(-x)互为相反数,f(x)为奇函数; 』也把重要的前提“定义域内恒有f(-x)=f(x),或恒有f(-x)=-f(x)”抛开来谈偶函数或奇函数。
如果象刘志斌那样不讲究“前提条件”,抛开重要的前提条件来判定函数的奇偶性,就很可能作出误判!
譬如,函数f(x)=√(x^2+2x+1)+√(x^2-6x+9) 定义域为(-∞,+∞),自变量在定义域内取一对儿互为相反的数值x、-x ,分别对应的函数值为f(x)、f(-x).
设 x=-1 则 -x=1 分别代入f( )=√[( )^2+2( )+1]+√[( )^2-6( )+9] 得:
f(x)=f(-1)=√[(-1)^2+2(-1)+1]+√[(-1)^2-6(-1)+9]
=√0+√16 = 4
f(-x)=f(1)=√[(1)^2+2(1)+1]+√[(1)^2-6(1)+9]
=√4 +√4 = 4
即 f(-x)=f(x) ,但是,我们不能像刘志斌那样因为该函数有f(-x)=f(x),就盲目的判定函数f(x)=√(x^2+2x+1)+√(x^2-6x+9) “为偶函数”!
我们马上就可以看到该函数的自变量取另一对儿互为相反的数值x、-x时,有f(-x)≠f(x) !
设 x=-2 则 -x=2 分别代入f( )=√[( )^2+2( )+1]+√[( )^2-6( )+9] 得:
f(x)=f(-2)=√[(-2)^2+2(-2)+1]+√[(-2)^2-6(-2)+9]
=√1 +√25 = 6
f(-x)=f(2)=√[(2)^2+2(2)+1]+√[(2)^2-6(2)+9]
=√9 +√1 = 4
即 f(-x)≠f(x),这就足以否定先前盲目作出的“f(x)为偶函数”之“判定结果” !
f(-2)=6;f(2)=4 很明显,f(-x)≠f(x),且f(-x)≠ -f(x)! 所以:
函数f(x)=√(x^2+2x+1)+√(x^2-6x+9) 既不是奇函数,也不是偶函数。
记号“y=f(x)”代表“y是x的函数”,有时简记作“f(x)”。当你定义 f(x)=logax 时,那就已经确立了函数f(x)的对应法则为:“y是x的对数”!法则记号“f( )”就代表“y是x的对数”!
在同一表达式或同一坐标系里,同一个记号“f( )”仅表示同一个“对应法则”!在表示“x的对数”这一对应法则的前提下,记号“f( )”就不应该用到y轴左侧的曲线上!
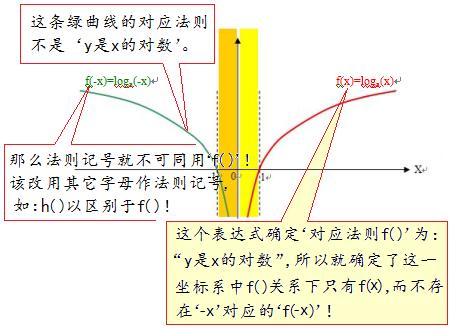
“x的对数”函数f(x),其定义域为:{ x│x>0 } ,这种“单边型”的定义域内根本不存在互为相反的数值。因此,对“x的对数”函数f(x)无从谈起“-x 对应的函数值f(-x)”!
323楼里,刘志斌分明是已经知道对于“x的对数”函数来说,f(-x)没有意义!
f(-x)没有意义,也就使表达式f(x)-f(-x)没有意义!使题目核心“求(f(x)-f(-x))/x<0时x的范围” 没有答案!!但是,刘志斌仍然不死心,仍然坚持胡搅:把不等式中的“f(x)” 对应成 f(x)=logax ,把同一式子中的“f(-x)”对应成 f(-x)=loga(-x) !
刘志斌坚持要把同一式子中的f(x)、f(-x) 胡搅成“两个函数”,完全不把教科书上的正统理论放在眼里!
如果要在同一个式子里表示两个不同的函数,就得使用不同的“法则记号”来对它们加以区别!这是起码的常识!
正统教科书解释“f(-x)”为“函数的值”即当函数y=f(x)的自变量在定义域内取一对互为相反的数值时,其自变量值“-x”所对应的“函数值f(-x)”!
当函数y=f(x)是偶函数时,函数值f(-x)≡函数值f(x)。即同一个函数在自变量取每一对儿互为相反的数的值时,俩自变量值分别对应的俩函数值都相等。也就是说偶函数自身是关于y轴对称的。
而刘志斌在325楼再次重复的坚持曲解“f(-x)”:“4、对于任意一个已知函数f(x),都有一个函数f(-x),函数f(-x)的图像与已知函数f(x)的图像以y轴为对称即f(x)=f(-(-x)):
即刘志斌曲解f(-x)不是原函数y=f(x)中的函数值,而是“另一个函数y=f(-x)”,两个函数以y对称。
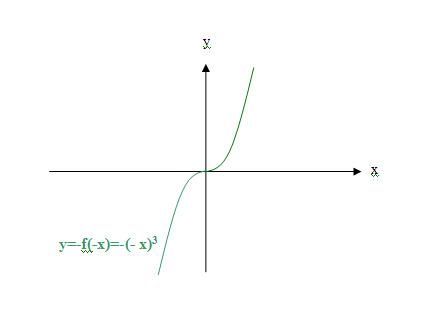
刘志斌以函数y=f(x)=x^2为例,荒谬地糊弄出所谓的“另一个函数y=f(-x)=(-x)^2 ”来以示区别于原函数y=f(x)=x^2 !
但凡明白数学的人们都能看出来:刘志斌这所谓的“另一个函数y=f(-x)=(-x)^2”,与原函数y=f(x)=x^2 根本就是同一个函数!
因为俩解析式清楚的表明:第1、它们的定义域相同,都是(-∞,+∞);第2、它们的值域相同,都是[0,+∞);第3、它们的对应法则相同,都是“因变量等于自变量的2次方幂”!3个要素都相同,充分证明它们是同一个函数!
要表达“因变量等于自变量的2次方幂”仅只用“f(x)=x^2”就足够了!
难道刘志斌还以为表示一个自变量名用一个字母x还不够吗?!还需要给自变量名“x”的前面再添个负号“-”才能完整的表达“因变量等于自变量的2次方幂”这一函数关系吗?!
326楼,刘志斌有继续的重复胡搅:“2)如果已知函数f(x)为奇函数,那么函数f(-x)的图像与已知函数f(x)的图像以y轴为对称,即f(x)=f(-(-x)),f(-x)也是个奇函数”
寒湘子曾经批评:刘志斌把同在一个不等式(f(x)-f(-x))/x<0中出现的记号f(x)
和f(-x)说成两个函数,这说明(刘志斌)没有弄懂函数的概念。
寒湘子所做的这个批评,是完全正确的!我们热烈的鼓掌支持!!
如果要在同一个式子里表示两个不同的函数,就得使用不同的法则记号来对它们加以区别!这是起码的常识!
刘志斌不懂这起码的常识,夹着屎犟说“1、f(x)和f(-x)是两个函数”!刘志斌自己没有弄懂函数概念,却反讥寒湘子没有弄懂函数概念!
寒湘子批评刘志斌时,所指的是题目核心的那个不等式‘(f(x)-f(-x))/x<0’中的函数值记号f(x)和f(-x)。这f(x)和f(-x)是同一个函数关系(即同一映射法则)下的俩函数值。
而刘志斌却胡搅的用两个不同映射法则的函数:y=x^3 和 y=-x^3 来搪塞!
下面这截屏图片是234楼刘志斌采取胡搅函数概念的贯用手段来搪塞刘自己将题目之不等式中‘f(-x)’曲解为‘有别于题设函数f(x)的另一个函数’这一谬误,所留下的证据:
我们以教科书上的正统理论为依据!请参阅教科书上的这段论述:
f(x)是奇函数的标志是:当自变量取一对互为相反的数的值时,函数的值也是互为相反的数,就是f(-x)= -f(x) .
这句“函数的值也是互为相反的数,就是f(-x)=-f(x)”. 非常明确的告诉我们:句中等式‘f(-x)= -f(x)’左右两边的记号‘f(-x)’和‘f(x)’都是同一个函数(譬如,y=f(x)=x^3)映射法则下分别和‘-x’、‘x’相对应的俩“函数值”!
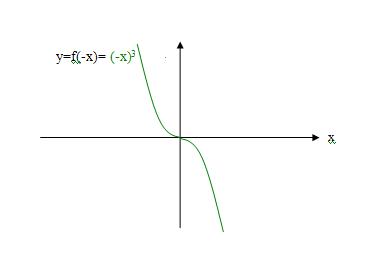
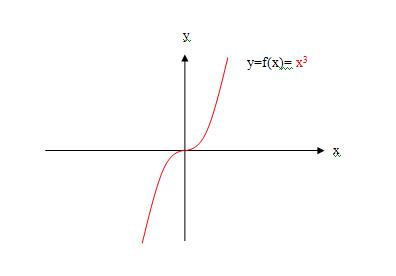
用上面的理论依据来分析刘志斌的这条曲线y=f(x)=x^3 :
奇函数、偶函数上所表现的对称性是对一个函数自身曲线分布在y轴左右两侧的两部分而言的,并不是指两个函数的相互对称性 !
刘志斌把表示同一条函数曲线上,位于y轴两侧且与y轴等距离的一对函数值的记号‘f(x)’和‘f(-x)’曲解为“两条曲线”、‘两个不同映射法则的函数’确实显露出刘志斌没有弄懂函数的概念!
用记号‘f(x)’表示函数y=x^3 时,有f(x)=x^3 ,对应法则f( )就表示“函数值是自变量的3次幂”(例如:刘志斌的红色曲线y=f(x)=x^3) ;
用记号‘f(x)’表示函数值时,法则记号‘f( )’括弧内的x代表自变量在定义域内任意的某个取值.
当需要表示自变量取定义域内任意的一对互为相反数的值所分别对应的俩函数值时,我们分别用‘x’和‘-x’填到记号‘f( )’的括弧内形成对应的俩函数值记号‘f(x)’和‘f(-x)’.
请注意:函数值记号‘f(x)’括弧中的内容x是函数定义域内任意的某一取值,所以,x既可以大于0,也可以小于0,还可以等于0.所以,函数值记号‘f(-x)’括弧中的内容‘-x’并不一定代表负数!且括弧中的内容‘-x’的负号也并不代表“映射法则的含义”!它仅仅只是相对于自变量任意的某一取值‘x’而言的相反数的记号而已!
‘f(-x)’的映射法则,仍然还是‘f(x)’的映射法则—‘f( )’!以y=x^3为例来说,都是“函数值=自变量取值的3次幂”!
例如,当x=2时,f(x)=f(2)=2^3=8 ,则f(-x)=f(-2)=(-2)^3=-8 .
很明显:坐标为(2,8)即(2,f(2))的点p在y=x^3曲线上(第1象限);坐标为(-2,-8)即(-2,f(-2))的点p' 同样的也在y=x^3曲线上(第3象限) .
也就是说,f(x)=x^3与f(-x)=(-x)^3是同一个函数y=x^3 上的俩函数值!刘志斌却故弄玄虚的搅出一条在2、4象限的曲线来楞充f(-x)=(-x)^3 ,难道在“刘志斌理论”里,点p'(-2,-8) 不在第3象限上?!
连高中学生都知道 ,凡横纵坐标皆小于0的点都必定在第3象限!可刘志斌却不懂得这个很基础、很简单的知识!愣要打胡乱说:f(-x)=(-x)^3 不是曲线y=x^3上的函数值(y=x^3曲线上的点p'(-x,f(-x))的纵坐标f(-x),参见上面的分析图曲线上的p'点)!
记号‘f(-x)’原本是人们在研究讨论函数奇偶性问题时引用的一个‘函数值’记号。表示同一函数当自变量在定义域内取一对互为相反数‘x’和‘-x’时,其中‘-x’所对应的‘函数值’。
刘志斌弄不懂‘f(-x)’的概念,指鹿为马的把曲线y= -x^3标成“f(-x)=(-x)^3”就堂而皇之的把同一条曲线y=x^3上点p'(-x,f(-x))’的纵坐标‘f(-x)’歪曲成另一条曲线y= -x^3 。却以自己的曲解为“准绳”,迫寒湘子举例来证明这两条不同映射法则的曲线不是两个函数!
这里要说明一点:楼主的题目所设的函数f(x)并不是y=x^3,也不是y=-x^3.刘志斌是用这两条不同映射法则的曲线来胡搅题目之不等式“(f(x)-f(-x))/x<0”中的俩记号‘f(x)’和‘f(-x)’的概念。
刘志斌不懂:如果需要在同一个式子中表达不同映射法则的两个函数时,就得把两个不同的映射法则用不同的记号区分开来!譬如,对于函数y=x^3 其法则可采用f( )表示,再对于另一个函数y= -x^3 其法则就可采用另一个记号如g( ) 来表示.
例如:f(x)=x^3 ,g(x)= -x^3
记号‘y=g(x)’同样也是表示‘y是x的函数’,x既可以表示正数,也可以表示负数以及0,即:x可以表示自变量在(-∞,+∞)上的任意一个取值。
所以,在用记号y=f(x)或记号y=g(x)表示‘y是x的函数’时,完全不需要给自变量名‘x’前加一个负号‘-’!
只有在函数f(x)定义域内存在有互为相反数‘x’和‘-x’的前提下,当自变量取一对相反数‘x’、‘-x’时,才有分别对应的‘函数值f(x)’和‘函数值f(-x)’。
函数值记号‘f(-x)’括弧中的内容‘-x’表示自变量的取值,x前的‘-’号,仅仅只是相对于函数值记号‘f(x)’来说,表示两者各自对应的自变量取值是互为相反的数!‘-x’并不一定代表负数,‘-’号也不代表‘映射法则’!
对于函数g(x)= -x^3来说,其自变量同样可以在定义域内取任意一对互为相反的数的值‘x’和‘-x’,那末,这俩自变量值所分别对应的俩‘函数值’就是‘g(x)’和‘g(-x)’!
总之,在同一式子里不论是‘f(x)’与‘f(-x)’组成一对儿也好,或者‘g(x)’与‘g(-x)’构成一对儿也罢,它们都是表示同一函数当自变量取定义域内任意一对儿互为相反的数的值时所分别对应的俩‘函数值’!即同一函数曲线上分处于y轴左右两侧,且与y轴等距离的点的纵坐标。 并不是表示映射法则不同的两个函数!
函数的“单调区间”概念≠“定义域”概念!
函数是增函数还是减函数,是对定义域内某个区间而言的。请参见教科书的表述:
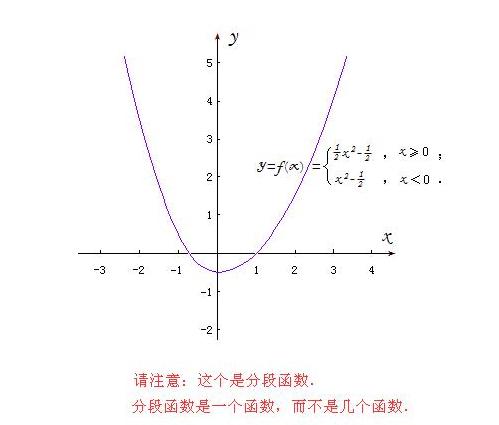
函数y=x^2 “在0到正无穷大是增函数”,难道刘志斌也可以曲解为函数y=x^2 的定义域是“在0到正无穷大”右半开区间?!难道刘志斌也可以曲解为函数y=x^2 的定义域是开区间(0,+∞) ?!
刘志斌曲解题设的函数f(x)定义域为(0,+∞) 是“多么可笑的”曲解!!
千万不能象刘志斌那样,单凭题目中提及函数“在0到正无穷大是增函数”,就荒谬的把函数的定义域判定为“在0到正无穷大”!更不能象刘志斌那样把函数的定义域曲解为开区间(0,+∞) !
如果题目所指的函数f(x)的定义域真的是“在0到正无穷大”,或如刘志斌所曲解的开区间(0,+∞),那么,题目的核心内容“求(f(x)-f(-x))/x<0时x的范围”就毫无意义!
因为这不等式里的“f(x)”与“f(-x)”分别是自变量在函数f(x)定义域内的两个互为相反的数的值“x”与“-x”对应的成对儿“函数值”! 而“在0到正无穷大”右半开区间内,或开区间(0,+∞)内都绝无可能存在有与“x”相反的数“-x”! 也就理所当然的绝无可能存在成对儿的函数值f(x)与f(-x)共存 !
正因为题目核心内容要“求(f(x)-f(-x))/x<0时x的范围”,所以,题目所设函数f(x)的定义域绝不可能仅限于“在0到+∞”,必定延伸到x<0的区域!
“单调区间”概念与“定义域”概念是不同的两个概念!它们之间又联系又有区别!
自变量可能取的值的全体叫做函数的“定义域”。也可以说“使函数有意义的一切实数的全体叫做函数的定义域”,大多数的函数定义域可以用x轴上的区间来表示。
而“单调区间”是“定义域”上的区间:如果对于“定义域”内的某个区间的任意两个自变量值x1、x2,当x1<x2时,f(x1)<f(x2),那么就说f(x)在这个区间是增函数;当x1<x2时,f(x1)>f(x2),那么就说f(x)在这个区间是减函数。而这个区间就叫做函数的“单调区间”。
它们之间的联系是:单调区间⊆定义域, 也就是说“单调区间”可以是“定义域”的一部分,也可以是“定义域”的全部。即“单调区间”是“定义域”的子集!
若“定义域”内至少有一个元素不属于“单调区间”时,则“单调区间”就叫做“定义域”的真子集。
合格的高中学生都能看懂题目中的“f(x)在0到正无穷大是增函数”是不可分割的一个单句!它只表达“函数f(x)在半开区间[0,+∞)上有单调递增的性质”,它并不是表达函数f(x)的定义域为开区间(0,+∞) ! 我们看看329楼刘志斌这荒谬的逻辑:
难道刘志斌认为『因为“f(x)在0到正无穷大是增函数”,“求(f(x)-f(-x))/x<0时x的范围”,所以f(x)的定义域为x>0 』? ! 刘志斌这是一个多么荒谬的“逻辑推演”?!
刘志斌把函数“单调区间”的概念混淆为函数“定义域”的概念是一个很低级的常识错误!
刘志斌妄图以对数函数在其“定义域”上全部都是“单调递增”的,来掩盖他把“单调区间”与“定义域”两个不同概念混淆起来的谬误,刘志斌在336楼故意的胡扯『1、函数的定义域可以是一个单调区间 ,举例说对数函数』。
题目所设函数f(x)的定义域必须有“关于0点对称”的区间,才能符合有“(f(x)-f(-x))/x<0时x的范围”!这就充分说明题目中的“单调递增”的区间[0,+∞)仅仅是题设函数f(x)定义域的“真子集”!你刘志斌能说这个“定义域的真子集”就是“定义域的整体”吗?!
难道刘志斌认为对数函数f(x)=logax 的定义域内能够允许互为相反的数x、-x共存吗?!对数函数f(x)=logax 的定义域内没有互为相反的数值x、-x 共存,“x的对数函数”又哪有“(f(x)-f(-x))/x<0”之说? ! !
刘志斌故意的把题目“f(x)在0到正无穷大是增函数,f(1)=0,求(f(x)-f(-x)) /x <0时,x的范围”所给出的条件“f(x)在0到正无穷大是增函数”硬生生的拆分成:
1) f(x)在0到正无穷大; 2) 增函数;
这样刘志斌就堂而皇之的把原题目修改了!为他把“单调区间”混搅成函数的“定义域”而做了一个铺垫:
并且,咬定符合1)、f(x)在正无穷大;2)、增函数;3)、f(1)=0,的函数f(x)只有对数函数logax a>1,
其实,对数函数y=logax a>1,的“定义域”也并不百分之百符合“0到正无穷大”!因为对数函数y=logax a>1的定义域并不包含0!而题目中“在0到正无穷大”是包括了0的!
况且,题目所指的函数f(x)在x<0的区间里也是有定义的,因为题目核心内容是“求(f(x)-f(-x))/x<0时x的范围”,说明题设函数f(x)的定义域内有互为相反的数值共存的区域。这也说明对应法则为“y是x的对数”的这种“单边型定义域”的函数绝不是这个题目所设的函数f(x) !
- 工控机和普通PC的区别
 [11419]
[11419] - 离心式水泵扬程H、流量Q、转速...
 [21312]
[21312] - 怎么判断三相电的三相?
 [13226]
[13226] - 交流接触器资料中AC-1 AC-2 ...
 [12218]
[12218] - 装机功率是什么啊?怎么计算?...
 [18034]
[18034] - 零线电流大于火线电流
 [20162]
[20162] - 请问星三角启动有时间继电器...
 [20478]
[20478] - 星三角启动电机烧毁原因请教...
 [12021]
[12021] - 48v电动车充电器12Ah和20Ah有...
 [12449]
[12449] - 『原创』如何制作动画教程
 [13614]
[13614]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号





















 工控网智造工程师好文精选
工控网智造工程师好文精选
