昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
引用 煙雨朦朦 的回复内容：
行了！晕！不懂就不要讨论了！……
1、满篇都是 煙雨朦朦的“理论”，自相矛盾的“理论”，晕是必然的结果！
2、我讲的很清楚，
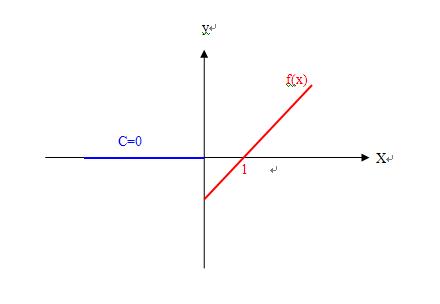
1）设函数f(x)在（0，＋∞）上是增函数，且f(1)=0，如图：
则当0＜x＜1，f(x)＜0，有 f(x)/x＜0；
2）将f(x)以y轴为对称轴翻转180°，得到函数f(-x)在（-∞，0）上是减函数，且f[-(-1)]=f(1)=0；
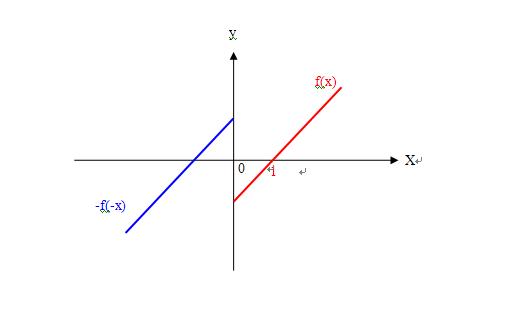
3）将f(-x)以x轴为对称轴翻转180°，得到函数-f(-x)在（-∞，0）上是增函数，且-f[-(-1)]=-f(1)=0：
则当-1＜x＜0，-f(-x)＞0，有 -f(-x)/x＜0；
4）设函数g(x)=f(x)-f(-x)，则
x＞0时，g(x)=f(x)；
x＜0时，g(x)=-f(-x)；
这样g(x)/x=[f(x)-f(-x)]/x，
在区间-1＜x＜0，g(x)/x=-f(-x)/x＜0
在区间 0＜x＜1，g(x)/x=f(x)/x＜0
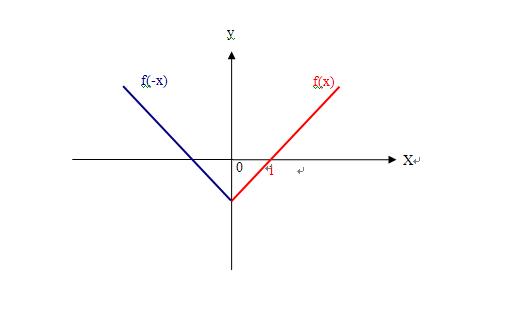
5） 如图
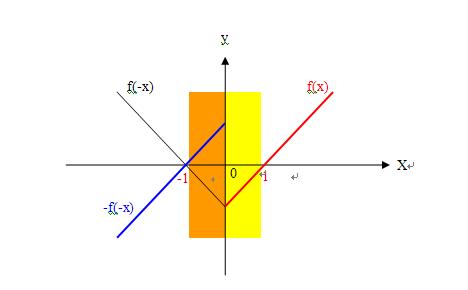
根据刘老师的观点：设函数f(x)在（0，＋∞）上是增函数，且f(1)=0，如图：
则当0＜x＜1，f(x)＜0，有 f(x)/x＜0；
但是题目是解不等式(f(x)-f(-x))/x<0
当0<x<1，假设x=0.5上述左边就应该表示为(f(0.5)-f(-0.5))/0.5，依题意我们知道f(0.5)<0,x>0但是f(-0.5)根据题目我们不知道，也就是没有定义。既然没有定义，就可以任意指定。我们选取f(0.5)-f(-0.5)>0即只要f(-0.5)<f(0.5)，左边函数值就是正的，这样0<x<1就不是问题的解。因为题目给出的是一般函数，对于x<0的f(x)性质没有定义。该题目“不完备”，题目无法求解！
从刘老师论述我们可以知道：“第一，刘老师不知道><=的数学含义，能够比较的数必有意义；第二，刘老师不清楚函数的定义，和数学符号f(x)的用法”！
引用 煙雨朦朦 的回复内容：
…当0<x<1，假设x=0.5上述左边就应该表示为(f(0.5)-f(-0.5))/0.5，……
1、当0<x<1，假设x=0.5上述左边就应该表示为f(0.5)/0.5，f(0.5)小于0，是负数，所以f(0.5)/0.5＜0；
当-1<x<0，假设x=-0.5上述左边就应该表示为-f(0.5)/-0.5，-f(0.5)大于0，是正数，所以-f(0.5)/-0.5＜0；
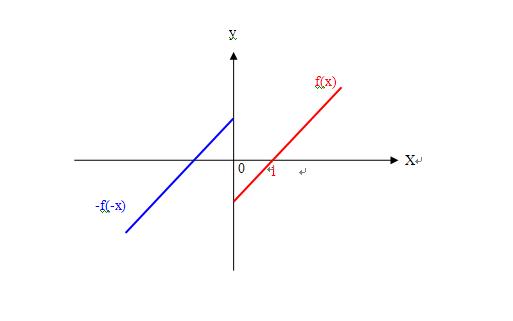
2、就好像煙雨朦朦给的函数，
在x=0.5时，f(0.5-ξ)＜f(0.5)＜f(0.5+ξ)，而不是f(0.5-ξ)=f(0.5)=f(0.5+ξ)=0，煙雨朦朦你说是吧？？？
在x=-0.5时，f(-0.5-ξ)=f(-0.5)=f(-0.5+ξ)=0，而不是f(-0.5-ξ)＜f(-0.5)＜f(-0.5+ξ)，煙雨朦朦你说是吧？？？
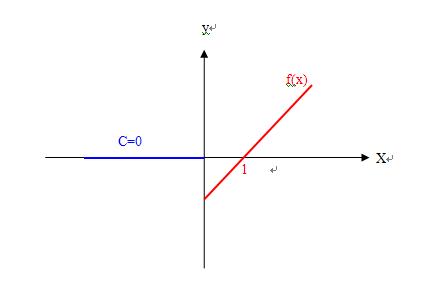
3、你知道煙雨朦朦错在什么地方？
1）题设f(x)的定义域是x＞0，这样-f(-x)的定义域是x＜0，如图
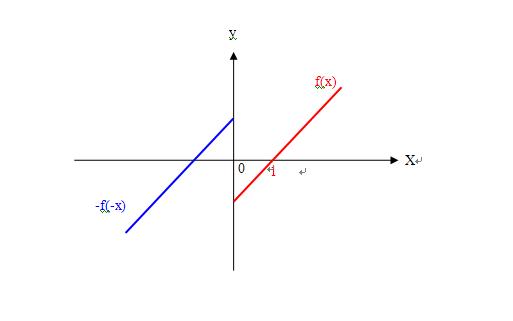
2）当x=0.5时，x在f(x)的定义域x＞0上，不在-f(-x)的定义域x＜0上；
3）所以f(0.5)是有定义的，是个小于0的负数，-f(-0.5)没有定义，所以f(x)-f(-x)/x=f(0.5)/0.5＜0；
4）煙雨朦朦的“假设x=0.5，……(f(0.5)-f(-0.5))/0.5，”，没有考虑题设函数的定义域，所以出现了错误；
5）是煙雨朦朦不知道吗？煙雨朦朦早就知道了，辩论这么长时间，说了无数遍，怎么能不知道呢？！
6）这就叫故意混淆是非，故意制造事端，……
节前，路过，凑个热闹。现在回头看下这个题目争论的逻辑。
题目如下：
f(x)在0到正无穷大是增函数，f（1）=0，求（f(x)-f(-x)）/x<0时x的范围
这里涉及到几个基本概念：函数、增函数、函数的值、函数的表示法。如果对这几个概念没有清晰的概念。就没有办法求解这个题目。因为函数定义的是两个数集的映射关系。f(x)和f(-x)实际是一个函数。当一个表达式为f(x)-f(-x)，f(x)是当自变量取x时函数的数值，同时f(-x)是自变量为-x时函数的数值，是两个互为相反数做自变量函数值的差。显然依代数规则只有当减数和被减数都有意义时才能求差。
显然，根据题目条件，无法比较以互为相反数为自变量函数值的差的正负。2楼认为题目条件不足是对的！
我们看136楼的函数和图像，这正是刘老师没有搞清楚的地方。
2、举例说 ，y= x-1和y= -x-1是两个函数，两个函数的图像以y轴
函数的解析式肯定和图片的函数图像不一致：
红色射线显然是y=f(x)=x+1函数的一段，因为f(0)=-1、f(1)=0这两点都落在射线上。但是蓝色射线显然就不是f(x)，因为f(x)是哪条红射线？是什么呢？如果是f(-x),那么就不对了。显然f(-1)=-1-1=-2而不是f(-1)=0.所以y=-x-1就不是f(-x)当然不是同一个函数了！
之所以产生这样的错误，原因在于：不清楚函数的表示。一个坐标系上不可能有两个都叫f（）的不重叠函数图像！
f() 的意思是"fuction of ()"与（）内容无关，定义的是一种映射关系。关系不变函数就是同一个函数。如果不承认这点，就没有办法进行函数演算。
引用 寒湘子 的回复内容：
……蓝色射线显然就不是f(x)，因为f(x)是哪条红射线？是什么呢？如果是f(-x),那么就不对了。显然f(-1)=-1-1=-2而不是f(-1)=0.所以y=-x-1就不是f(-x)当然不是同一个函数了！
1、 红色射线显然是y=f(x)=x+1函数的一段，因为f(0)=-1、f(1)=0这两点都落在射线上。
2、同理，“蓝色射线显然就不是f(x)”，蓝色射线是f(-x)的图像，因为f[-(-1)]=f(1)=0，f[-(0)]=f(0)=-1，这两点都落在蓝色射线上；
3、“蓝色射线……如果是f(-x),那么就不对了。显然 f(-1)=-1-1=-2而不是f(-1)=0.所以y=-x-1就不是f(-x)当然不是同一个函数了！”，是寒湘子在胡言乱语！
假如我们知道：
f()=()+1/()我们就有f(x)=x+1/x,f(-x)=-x-1/x,f(1)=1+1/1=2,f(-1)=-1-1/1=-2.如果我们认为函数f(x)和f(-x)是不同的函数。我们怎么能根据f(1)=0断言f(-(-1))=0呢？
函数定义的是映射关系f,g,h等等。有了映射关系便可以求f(x),f(1/2x),f(0.5),f(-8)等等的函数值。函数值不相等并不等於函数不同啊。同样f(x),f(-x)也不过是函数f关系下取x和-x的两个函数值而已。对于根据题目不能确定的量，可以忽略不计，视若无物？
有那条代数和算术原理，支持这样的处理？
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
