昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
11、1次幂函数，就是我们常说的正比函数，实际问题中，如果y是总价，x是数量，那么系数就是单价，单价是1，也可以是2、3、……；
12、我们大家对幂函数感觉很生疏，原因是我们平常不叫“幂函数”这个名字，常常叫它的其它名字，举例说正比函数、反比函数、1次函数、2次函数、3次函数、等等；
13、指数函数、幂函数都是关于“幂”或者叫“乘方”的运算，幂底数是变量者为幂函数，幂指数为变量者为指数函数；
14、在研究基本初等幂函数时，给了一个特定意义的定义式，得出了有关这个定义式的幂函数的结论，依次逐类旁通，对于非特定定义式的幂函数的图像、定义域值域、性质、特性可以照此求得解答！
15、而不能像 煙雨朦朦 理解的“系数不是定义式的1，就不是幂函数。”！！！
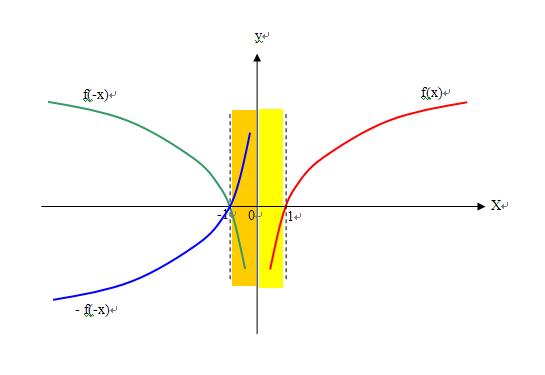
2、在（0，+∞）f(x)有意义-f(x)不存在，（-∞，0）f(-x)有意义f(x)不存在，（-∞，0）-f(-x)有意义f(x)不存在；而不是煙雨朦朦说的f(x)与f(-x)必然有一个无法确定！
3、当x＞0时，-f(-x)不存在，所以f(x)-f(-x)就是f(x)；
4、当x＜0时，f(x)不存在，所以f(x)-f(-x)就是- f(-x)；
如果在某一区间f(x)-f(-x)=f(x)，那么在这个区间f(-x)=0，就不能说f(-x)不存在；
如果在某一区间f(x)-f(-x)=-f(-x)，那么在这个区间f(x)=0，就不能说f(x)不存在；
刘老师岂不是自相矛盾？请问数学上f(x)或 f(-x)不存在，为什么按数学法则会等于0！除非刘老师的f(x)-f(-x)=f(x)，f(x)-f(-x)=-f(-x)，不成立！
不过，刘老师向来认为没有必要考虑逻辑的。就像需要从方程中证明幂函数一样！
如果我说刘老师没有学好数学，也许论坛各位，不能分辨！但是我将刘老师的论断整理成下列形式大家就可以理解其自相矛盾了！
当x＞0时，-f(-x)不存在，所以f(x)-f(-x)就是f(x)（数学表达：f(x)-f(-x)=f(x)）；
可是如果f(x)-f(-x)=f(x)，那么等式两边同时减去f(x)有-f(-x)=0即f(-x)=0。（代数公理：等量减等量差相等），这样就不能说-f(-x)不存在，这不是自相矛盾吗？
同理
当x＜0时，f(x)不存在，所以f(x)-f(-x)就是- f(-x)；必得到f(x)=0同样是自相矛盾！
但有意思的是刘老师自己竟然说：
“
3、这样函数：
当x＞0时，-f(-x)不存在，所以f(x)-f(-x)就是f(x)；这时不能说-f(-x)=0；
当x＜0时，f(x)不存在，所以f(x)-f(-x)就是- f(-x)；这时不能说f(x)=0；
”
除非刘老师不承认公理，那还谈什么呢？说以又回到我的那句话，如同和外星人对话！
引用 煙雨朦朦 的回复内容：
…… 如果f(x)-f(-x)=f(x)，那么等式两边同时减去f(x)有-f(-x)=0即f(-x)=0。（代数公理：等量减等量差相等），这样就不能说-f(-x)不存在，这不是自相矛盾吗？
1、那不是“代数公理”，那是方程的性质1，或者是等式的性质1，叙述的语言也不合常识；
2、“f(x)-f(-x)=f(x)”，是有条件的：x＞0，-f(-x)不存在；
3、煙雨朦朦推导时，忘了x＞0，-f(-x)不存在的题意，也就是忘了函数存在的定义域（-∞，0）；
4、“等量减等量差相等”，不等量减等量差相等吗？
5、煙雨朦朦这样的逻辑思维，寄希望于“也许论坛各位，不能分辨！”！
引用 煙雨朦朦 的回复内容：
……以刘老师认为“无意义”不是“不能确定”是没有搞懂我为什么说“不能确定”而不直接用”无意义“。……
1、 题意告诉函数f(x)的定义域是（0，∞），煙雨朦朦疑惑（-∞，0）时f(x)是个什么情况呢？
2、煙雨朦朦疑惑（-∞，0）时f(x)是个什么情况呢？然后就说“不确定”，所以此题无解！
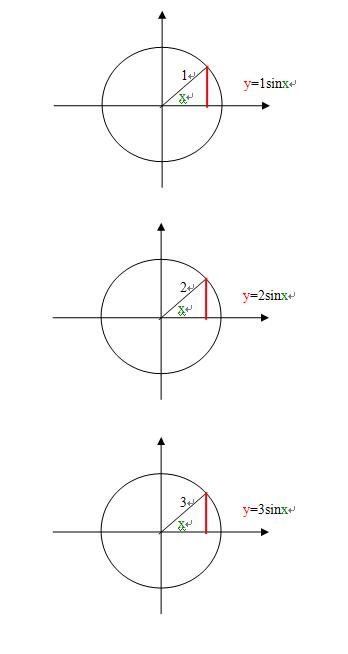
3、煙雨朦朦的“疑惑”说明煙雨朦朦的数学概念不清，这和煙雨朦朦说“y=sinx是正弦函数，y=2sinx还真不是正弦函数。”的错误的原因一样；
4、煙雨朦朦的“疑惑”说明煙雨朦朦的数学概念不清，这和煙雨朦朦说“y=x是幂函数，y=2x不是幂函数。”的错误的原因一样；
5、煙雨朦朦尽管知道自己是错误的，还要强辩，他寄希望于“也许论坛各位，不能分辨！”！
数学中对一些概念需要定义，如幂函数。没有定义就就不能进行演算和推理。定义是推理的基础。除了定义，有一些看似简单的东西，并非不证自明。选取最小的几个无法证明又是推理必须的命题作公理。其余的所有结论都必须由定义和公理推论得出。这样的一个系统方法就是数学公理化体系。《几何原本》就是最早的公理化体系，希尔伯特完善了公理化体系。数理逻辑也是建立在公理体系上的。牛顿的《自然哲学的数学原理》也借鉴了《几何原本》的架构。刘老师竟然能够对未定义的函数（在函数的未定义区间上）进行演算。那一定不是数学问题。在计算机程序里没有人能够对未定义的变量进行运算，道理是一样的。看来人比机器聪明，可以取巧，机器不能做的，人可以做，只要说“就是这样”就够了。管他合不合逻辑呢！另外没有“非定义域”的概念，正确的讲法因该是“函数的未定义区间”，既然未定义怎么运算。既然等式成立，为什么不能用“公理”推论？我讲“等量减等量其差相等”是公理，不是我的发明，这是代数的基本关系：如果a=c，那么a-b=c-b。的文字简述。要不刘老师给出一个证明吧！这是“命题”而不是“定义”，如果不成为公理，你就必须用更简单的“公理”和“定义”给出证明！另外楼主的题目与对数函数没有一毛钱关系，总是用那么一个图，翻来复去来捣鼓自以为是的“命题”，那么你给“命题”一个证明吧！请问，可与根据哪些定义和公理或定理可以推导出你的“命题”?
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
