假设函数f(x)的定义域为D.

　　一般地，如果对于属于定义域D内某个区间上的任意两个自变量值x1、x2，当

x1＜x2时，都有f(x1)＜f(x2)，那么就说f(x)在这个区间上是增函数；

　　如果对于属于定义域D内某个区间上的任意两个自变量值x1、x2，当x1＜x2时，都有f(x1)＞f(x2)，那么就说f(x)在这个区间上是减函数；

　　如果函数f(x)在某个区间上是增函数或减函数，就说f(x)在这个区间上具有(严格的)单调性，这个区间叫做f(x)的单调区间。

　　有两点须得注意：

　　1、函数的单调性是对某一个区间而言的，这个区间不必是函数的定义域，而常常是定义域的某一部分。

　　2、在增(减)函数的定义中，x1, x2 是任意的，这一点非常重要，绝不能忽视，其本质就是把比较区间上无限多个函数值的大小比较问题转化为两个任意的函数值的大小比较。

　　请注意：函数f(x)的“单调区间”的概念并不是“定义域”的概念！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　题目中函数f(x)的对应法则“f( )”具体含义不明确时，该题目的解就可能不是唯一的。正因为该题目中f(x)的对应法则“f( )”具体含义不明确，我们便可以把它转化为我们解题时的“有利条件”：

　　只需我们随便举出一例符合该题意的某一个函数f(x)的具体法则“f( )”，并根据该例函数f(x)的法则“f( )”解出“(f(x)-f(-x))/ x ＜0 时x的范围”即可作为该题目的“正确答案”！

　　对于楼主这个题目“f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x<0时x的范围”应该根据题目语境来判定该题目中符号“f(x)”的意涵。

　　对于“f(x)在0到正无穷大是增函数”这一句中的符号“f(x)”应该判定为：符号“f(x)”表示x的函数。自变量为x，因变量为f(x) 。

　　对于“求(f(x)-f(-x))/x <0 时x的范围”这一句中符号“f(x)”及“f(-x)”则应该判定为：同一函数f(x)其自变量取任意的互为相反的数值所分别对应的成对儿“函数值”。即同一个函数中“函数值f(x)”及“函数值f(-x)”。

　　同一个符号“f(x)”既可以表示“x的函数”，又可以表示“当自变量在定义域内取任意一个x值时，对应于该x值的 ‘对应函数值y ’”。

　　就好比《电工学》中，用同一个词“电流”既可以表示“电荷的有规则的定向运动”，又可以表示“单位时间内通过导体横截面的电荷量—电流强度”一样，一词多义。

　　楼主这个题目“f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x<0时x的范围”的正确答案可以有很多！

　　下面我给出一个正确答案供网友们参考：

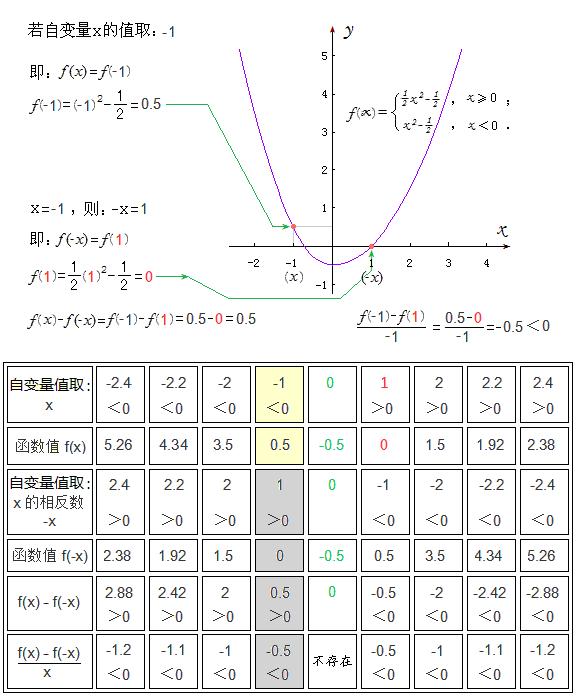
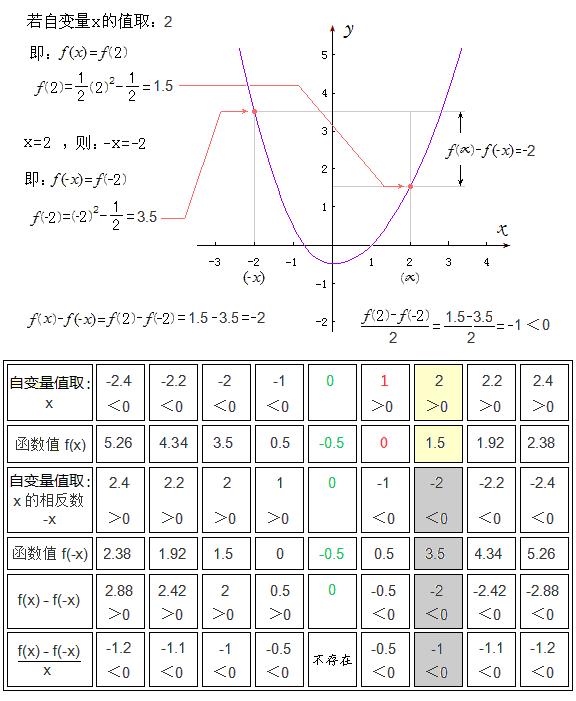
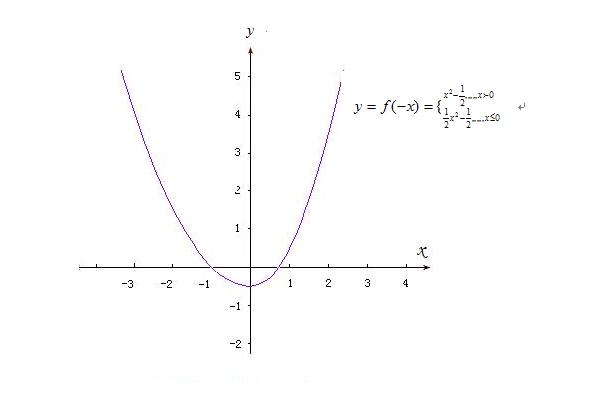
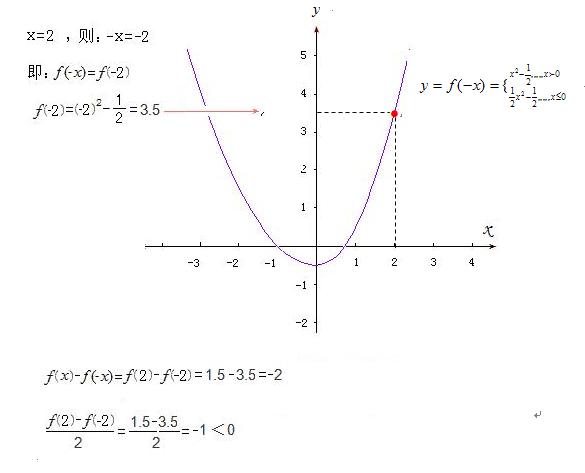
　　设有分段函数f(x)：

　　当自变量取值在(-∞，0) 区间上时，f(x)函数关系的对应法则为f(x)=f1(x)，

　　f1(x)=x^2 －0.5 ； 

　　当自变量取值在[0，+∞) 区间上时，f(x)函数关系的对应法则为f(x)=f2(x)，

　　f2(x)=0.5x^2－0.5 .

　　这就是一个既符合题目之题设“f(x)在0到正无穷大是增函数，f(1)=0”，又能让题目之核心部分中的那个不等式“(f(x)-f(-x))/x＜0”具有意义的函数f(x)。  

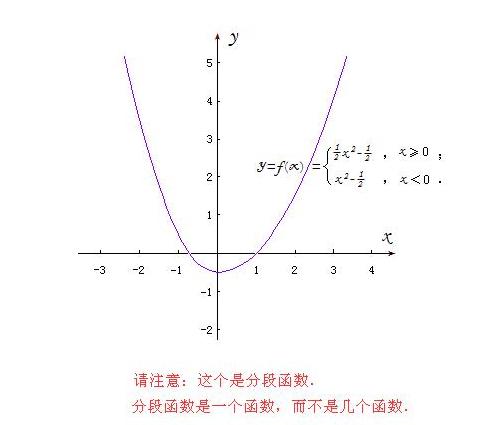
　　请网友们注意  ：分段函数在定义域的不同区间内，对应法则不同，但是，它仍然也只是一个函数，而不是几个函数！

　　我们把分段函数的“对应法则f( )”看成是分有层次的法则。对于本例函数，其总体层面上的对应法则为：f(X)=f1(x) ，(当x＜0时)；f(X)=f2(x) ，(当x≥0时) .

　　而其各分段层面上的对应法则为：f1(x)=x^2 －0.5 ； f2(x)=0.5x^2－0.5 .

　　现在老王来证明这个分段函数f(x)在0到正无穷大是增函数，且f(1)=0 . 

　　证明：设x1，x2 是[0，+∞)上任意的两点，且 x1＜x2 。

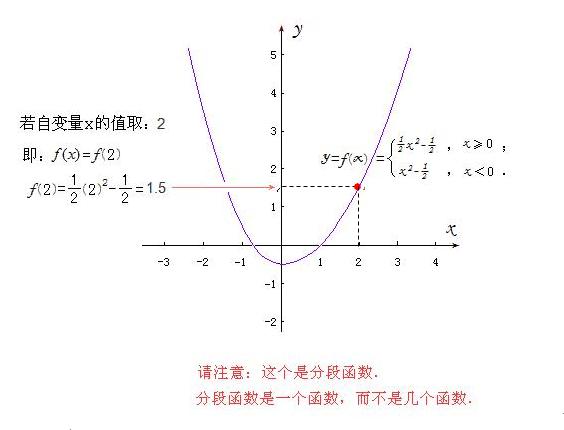
1)、∵当x在[0，+∞) 区间上时，f(x)函数关系的对应法则为 f(x)=f2(x)=0.5x^2－0.5  

　　则，f(x1)＝0.5(x1)^2－0.5　，f(x2)＝0.5(x2)^2－0.5   

　　∴　f(x1)－f(x2)＝(0.5(x1)^2－0.5)－(0.5(x2)^2－0.5)＝0.5((x1)^2－(x2)^2) 

　又∵  0≤x1＜x2　∴ (x1)^2－(x2)^2＜0　∴ 0.5((x1)^2－(x2)^2)＜0，即：f(x1)＜f(x2) 

2)、当自变量值x=1 时，对应的函数值f(1)＝0.5(1)^2－0.5＝0.5－0.5＝0 

所以，f(x)=0.5x^2－0.5 在“0到正无穷大”即[0，+∞)上是增函数，且f(1)＝0 。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　再证明该分段函数能让题目之核心部分中的那个不等式“(f(x)-f(-x))/x＜0”在x≠0的实数范围内具有意义。 

　　证明：设“x”、“-x”是函数f(x)定义域内任意的一对互为相反数的自变量值. 

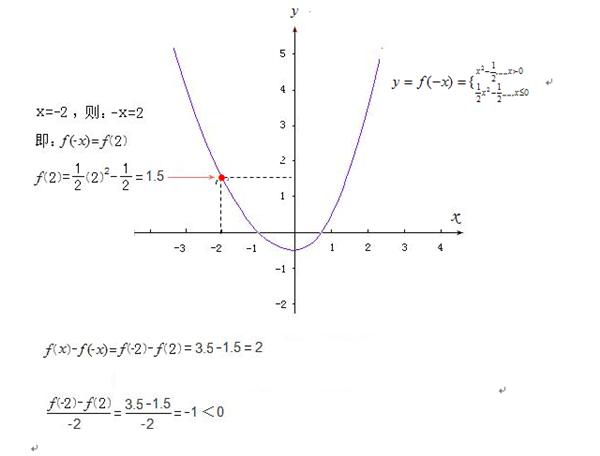
　　1)、当x＞0时，  则：-x＜0 ,　

　　那么，f(x)=0.5(x)^2-0.5 ；f(-x)= (-x)^2-0.5 

则：f(x)-f(-x)=(0.5(x)^2-0.5)-((-x)^2-0.5)

　　　　　  =(0.5(x)^2-0.5)-((x)^2-0.5)

　　　　　  =(0.5-1)(x)^2

　    　　　  = -0.5(x)^2＜0 

　　f(x)-f(-x)＜0，而x＞0，

即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立；

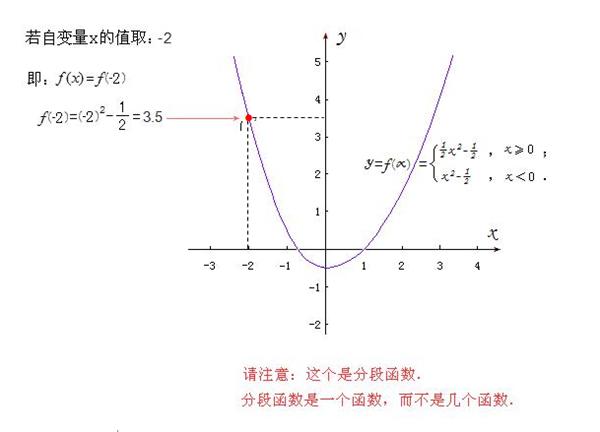
　　2)、当x＜0时，  则：-x＞0 ,　

　　那么，f(x)=(x)^2-0.5 ；f(-x)=0.5(-x)^2-0.5 

则：f(x)-f(-x)=((x)^2-0.5)-(0.5(-x)^2-0.5)

　　　　　  =((x)^2-0.5)-(0.5(x)^2-0.5)

　　　　　  =(1-0.5)(x)^2

   　 　         =0.5(x)^2＞0 

　　f(x)-f(-x)＞0，而x＜0， 

即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立。

　　所以，对于该分段函数f(x)有：自变量取除0之外的一切实数都能使不等式

“(f(x)-f(x))/x＜0”成立！

　　即：对于该分段函数f(x)来说，(f(x)-f(-x))/x＜0时x的范围是“除0之外的一切实数”。 

　　我们再列一组具体的数据来抽查检验一下这个分段函数是否符合题意，是否能让题目核心部分的那个不等式“(f(x)-f(-x))/x＜0”具有意义：

　　通过以上表格数据的抽查，抽查结果符合题意：f(x)在0到正无穷大是增函数，　f(1)=0,    且能让不等式(f(x)-f(-x))/x＜0 有获得‘成立’的范围！

　　可以看出，此例函数在(f(x)-f(-x))/x＜0时x的范围是“除0之外的一切实数”。

回复内容：

对： wanggq  　　　　也许有网友会认为：题目中有“f(x)在0到正无... 内容的回复！

 同意220楼的观点！

引用 wanggq 的回复内容： 　　　

      也许有网友会认为：题目中有“f(x)在0到正无穷大是增函数”这一句子就说明该函数f(x)的定义域是“0到正无穷大”。

      但是，这种认为是错误的。

      这一句子只能表达该函数f(x)在定义域内的“0到正无穷大”区间内的“单调性”是增函数。并不是表达该函数f(x)定义域为：“0到正无穷大”。

1、作为解题者，只能依据题意解题；

2、原题目的已知条件是“f(x)在0到正无穷大是增函数，f(1)=0，”，说明函数在区间“0到无穷大”上，是已知函数f(x)的定义区间；

3、仔细阅读题目，我们再没有任何信息和理由把“0到正无穷大”作为函数定义域的一个单调区间；

4、我们更没有理由猜想已知函数f(x)，“在0到负无穷大”是个什么函数，甚至自己给已知函数f(x)补充上“0到负无穷大”区间，这样还没有解题，就犯了错，更谈不上有什么正确答案！

引用 wanggq 的回复内容： 

……

对于“求(f(x)-f(-x))/x <0 时x的范围”这一句中符号“f(x)”及“f(-x)”则应该判定为：同一个函数f(x)中的俩“函数值”。即同一个函数中“函数值f(x)”及“函数值f(-x)”。

……

1、这个题目已知的是一个函数f(x)，要求的是“求(f(x)-f(-x))/x <0 时x的范围”，f(-x)是什么函数呢？题目中没有任何说明；

2、如果谁熟悉函数f(x)和函数f(-x)的相关知识，并能根据已知函数f(x)求得函数f(-x)，谁就会解这道题，如果一无所知，胡乱猜想，必然会出大笑话！

3、 wanggq 说“f(x)”及“f(-x)”则应该判定为：同一个函数f(x)中的俩“函数值”。即同一个函数中“函数值f(x)”及“函数值f(-x)”。

4、说明 wanggq压根就不懂函数f(x)和函数f(-x)的相关知识，结果就出现了给原题目已知函数f(x)补充了“0到负无穷大”区间上的“分段函数”……

引用 wanggq 的回复内容： 　　　

   ……

       楼主这个题目“f(x)在0到正无穷大是增函数，f(1)=0，求（f(x)-f(-x)）/x<0时x的范围”的正确答案可以有很多！

   ……

1、 多么可笑的一段话，你想想，给原题目已知函数f(x)补充“0到负无穷大”区间，在“0到负无穷大”区间上再随意补充一个分段函数，那还能不是“正确答案可以有很多！”

2、我们先看看 wanggq 给原题目补充的分段函数，以及所谓的正确答案：

3、下图是 wanggq 给原题目已知函数f(x)补充分段函数；

4、我来做 wanggq 补充后的这道题：

1）根据已知分段函数f(x)，求出函数f(-x)也是一个分段函数，如图

2）然后求函数 f(x)-f(-x) ，在0到负无穷大区间，举例1，

3）然后求函数 f(x)-f(-x) ，在0到正无穷大区间，举例2

从上两例可以看出，这个题目（f(x)-f(-x)）/x<0时x的范围为(-∞，0)、(0，+∞)

5、以上解题过程是我做的过程，与wanggq 的过程和方法不用，wanggq 是在同一个分段函数上，取自变量x、-x互为相反数对应的函数值f(x)、f(-x)的差；函数值f(x)为y轴右边的图像上的函数值，函数值f(-x)为y轴左边的图像上的函数值；

6、以上解题过程是我做的过程，我的方法是在用函数f(x)和函数f(-x)的差运算函数 f(x)-f(-x)，代入同一个自变量x，求得答案；

7、wanggq 的过程和方法是错误的，wanggq认为“符号“f(x)”及“f(-x)”则应该判定为：同一个函数f(x)中的俩“函数值”。即同一个函数中“函数值f(x)”及“函数值f(-x)”。

8、而 符号“f(x)”及“f(-x)”不是同一个函数f(x)中的俩“函数值”， “f(x)”和“f(-x)”是两个不同的函数，

 f(x)-f(-x)是两个函数“f(x)”及“f(-x)”的差运算函数；

引用 寒湘子 的回复内容：

……说f(x)和f(-x)是两个函数肯定是错的。这说明没有弄懂函数概念。

1、f(x)和f(-x)是两个函数，寒湘子说“f(x)和f(-x)是两个函数肯定是错的”，说明寒湘子没有“弄懂函数概念”

2、举例说，函数f(x)=x^3和f(-x)=(-x)^3是两个函数，因为

1）解析式不同，一个函数解析式是f(x)=x^3，另一个函数解析式是f(-x)=(-x)^3；

2）图像不同，如下图：

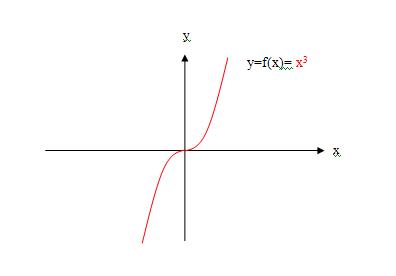
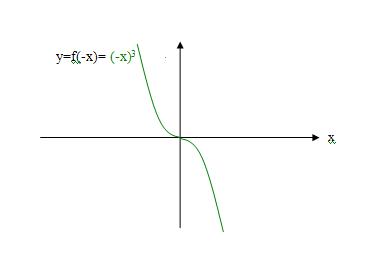
3）函数的性质不同，函数y=f(x)=x^3，在1象限，增函数；函数y=f(-x)=(-x)^3，在4象限，减函数；

……

3、请寒湘子举一例说明，f(x)和f(-x)不是两个函数！

引用 wanggq 的回复内容： 　

“f(x)在0到正无穷大是增函数”仅仅只能说明该函数f(x)在半开区间 [0，+∞）具有“单调增加”的性质而已！并不是该函数“定义域”的完全信息！

1、 <研讨会宣传员-3259>的题目是：

f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x<0时x的范围   

2、wanggq 为什么要睁着眼说瞎话呢？函数f(x)的“定义域”的完全信息是题目给定的“在0到正无穷大”，而不是由解题的人wanggq胡说八道随意补充的！

3、寒湘子和wanggq 不懂这个规矩吗？寒湘子和wanggq 忘了自己是解题者，而不是出题者，解题的人只能根据题设条件解题，不能随意更改题目！

4、那么对数函数lgx，就是满足题意“f(x)在0到正无穷大是增函数，f(1)=0，”的一个函数，如图

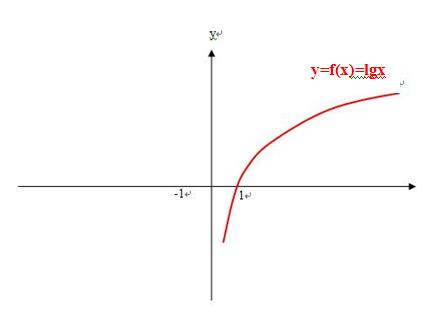
5、而寒湘子和wanggq 所说的那个分段函数，恰恰不是题设条件的函数，那么这种不符合题意的解题过程和答案还有什么意义呢！

6、题目“求(f(x)-f(-x))/x<0时x的范围   ”，当然是要根据题设已知函数f(x)先求出函数f(-x)、-f(-x)及f(x)-f(-x)，最后才能确定“(f(x)-f(-x))/x<0时x的范围 ”

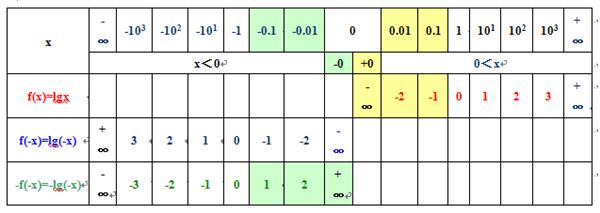
1）题设已知函数f(x)在0到正无穷大是增函数，f(1)=0，如图

2）则求得函数f(-x) 在0到负无穷大是减函数，f(-(-1))=0，如图

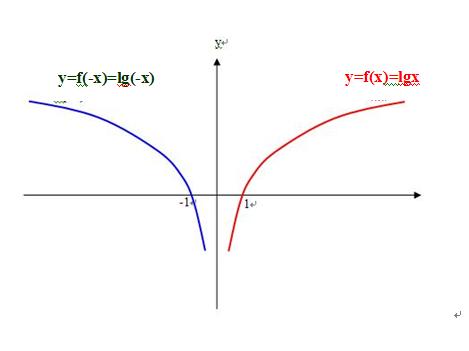
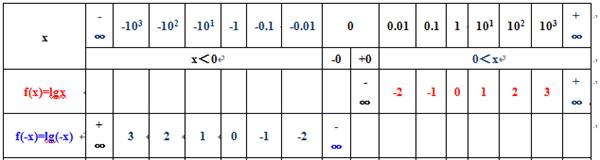
3）则求得函数-f(-x) 在0到负无穷大是增函数，-f(-(-1))=0，如图

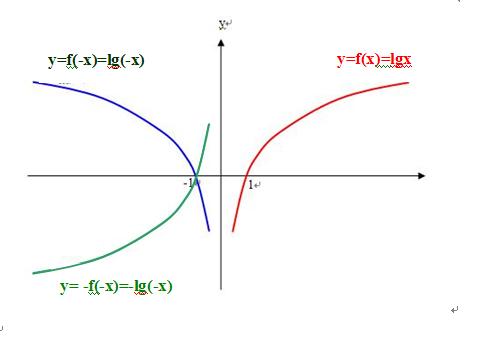
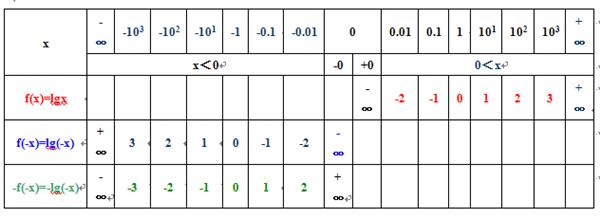
4）则求得函数f(x)-f(-x) 在区间(-∞，0)、(0，+∞)上是增函数，-f(-(-1))=0，f(1)=0，

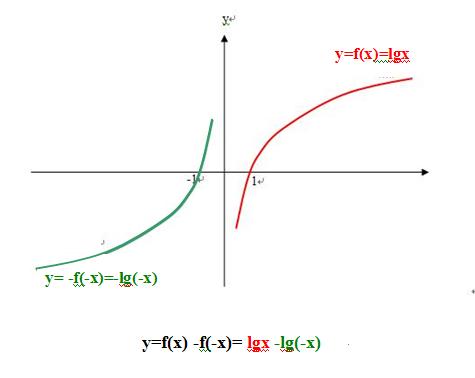
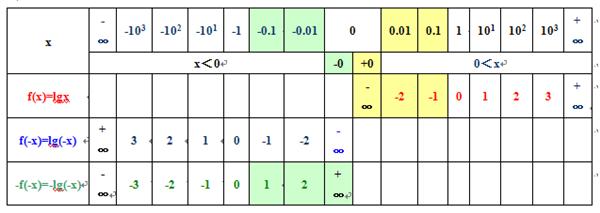
5）最后确定“(f(x)-f(-x))/x<0时x的范围 ”，

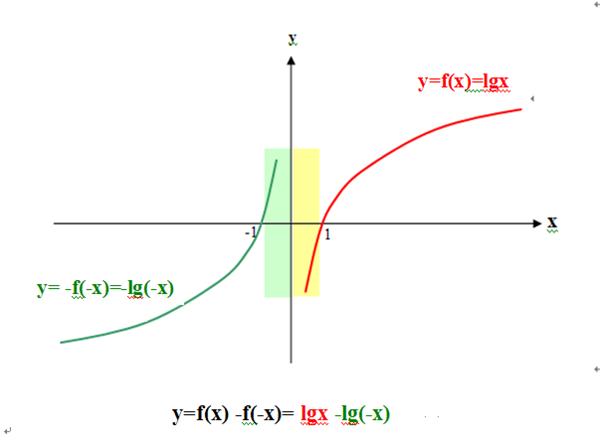
在区间(-1，0) 上，  (f(x)-f(-x))/x=-f(-x)/x<0；

在区间(0，1)上，(f(x)-f(-x))/x=f(x)/x<0。

如图：

引用 wanggq 的回复内容：   　

……　刘志斌还是想掩盖他把函数f(x)当自变量取一对互为相反数的值（x和-x）时，分别对应的“函数的值f(x)”及“函数的值f(-x)”误当成两个“函数”的错误！继续的胡搅：把老王举例用的偶函数（注意：该偶函数也只是一个函数，并不是两个函数噢）在y轴左边的图象说成可以是另一个函数y=f(-x)　!

1、 函数f(x)，就是自变量为x时的函数值， wanggq 不明白这个？！

2、自变量取一对互为相反数的值x和-x时，分别对应的“函数的值f(x)”及“函数的值f(-x)”，就是两个函数，与自变量x对应的函数值f(x)，就是函数f(x)；与自变量-x对应的函数值f(-x)，就是函数f(-x)；

3、“偶函数也只是一个函数，并不是两个函数噢”，是啊，这个也真难为 wanggq 了，说明 wanggq 真的不懂！

4、wanggq记住，偶函数f(x)=f(-x)，说明偶函数的解析表达式可以是f(x)，也可以是f(-x)；

5、wanggq记住，偶函数f(x)=f(-x)，说明偶函数的图像，是偶函数f(x)的图像与偶函数f(-x)的图像以y轴对折完全重合而已；

6、wanggq记住，偶函数f(x)=f(-x)，说明函数f(x)是一个偶函数，那么同时说明函数f(-x)也一定是个偶函数，所以偶函数，一定是两个偶函数！

7、举例说，函数y=x^2是一个偶函数，那么函数y=(-x)^2也是一个偶函数，是不是两个函数？f(x)和f(-x)总是两个函数，偶函数时，f(x)=f(-x)，两函数图像重合而已！如下图

↓

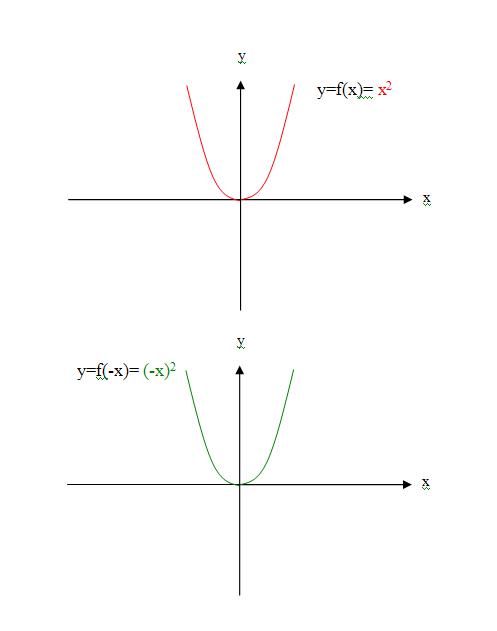
下来我讨论一下，寒湘子举例函数f(x)=1/x和函数f(-x)=1/(-x)，是不是一个函数？

1、已知函数f(x)=1/x，如图

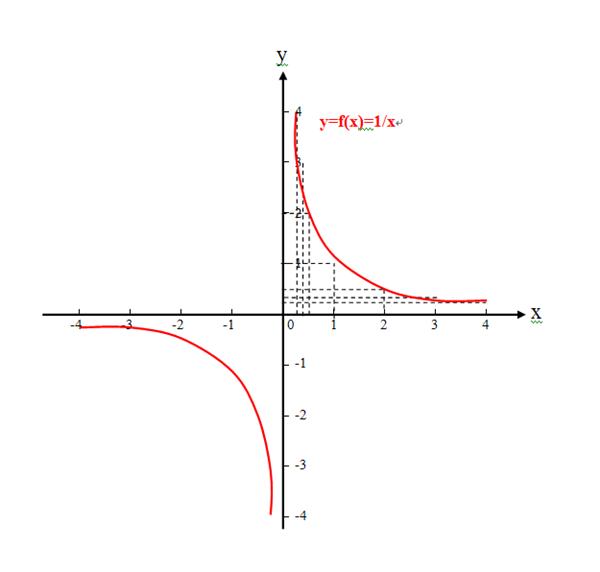
2、依据已知函数f(x)=1/x，求得函数f(-x)=1/(-x)，如图

3、寒湘子说“函数的三个要素是定义域、值域、对应关系”，那么函数f(x)=1/x和函数f(-x)=1/(-x)是不是一个函数？

1）函数f(x)=1/x的对应关系是f( )=1/( )，函数f(-x)=1/(-x) 的对应关系是f(-( ) )=1/(-( ) )，所以要素之一“对应关系”不同，后者对自变量x有一个求反的过程；

2）显然，函数f(x)=1/x和函数f(-x)=1/(-x)不是一个函数，而是两个函数；

3）不过，函数f(x)=1/x和函数f(-x)=1/(-x)是两个相关函数，函数f(x)=1/x是已知函数，函数f(-x)=1/(-x)是由已知函数f(x)=1/x对自变量x求反得出的，图像是与已知函数图像以y轴为对称的；

4）不知寒湘子举此例，并没有说明白函数f(x)=1/x和函数f(-x)=1/(-x)是一个函数，想说明什么问题呢？

4、这个问题搞清楚了，主楼的题目就会迎刃而解，就知道f(-x)并不是已知函数f(x)图像y轴左侧的一个函数值，就不会再想着设法给已知函数补充另一半定义区间及其函数，……，就不会再出笑话！

　　但凡明白数学的人，都能看清老王在220楼的发言是正确的！楼主的题目“f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x＜0时x的范围”的核心部分“求(f(x)-f(-x))/x＜0时x的范围”说明了题设的函数f(x)的定义域内有“互为相反的数”！所以，题设函数f(x)的定义域并不是仅限于“在0到正无穷大”！而这个“在0到正无穷大”只是题设函数f(x)定义域内一个“有单调递增性质的区间”而已！

　　刘志斌弄不懂“单调区间”与“定义域”这两个不同概念之间的联系和区别，还恶意的诋毁老王的正确观点！

　　下面这幅截屏图片是刘志斌在228楼恶意的对老王正确观点进行诋毁的截屏证据：

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　函数是增函数还是减函数，是对定义域内某个区间而言的。有的函数在一些区间上是增函数，而在另一些区间上是减函数。

　　这是正统教科书上关于函数的单调性的知识：

　　刘志斌缺乏函数的基本知识，所以，刘志斌再怎么“仔细阅读题目”也不可能从中领悟到题目蕴涵着的“单调区间”之信息！

　　所以，刘志斌再怎么“仔细阅读题目”也不可能从中领悟到题目蕴涵着的“所设函数f(x)在x＜0的区间上也有定义”之信息！

　　刘志斌把函数f(x)的“单调区间”误解为“定义域”是在闹笑话！刘志斌是在明白数学的人们面前出洋相！

　　对于“求(f(x)-f(-x))/x <0 时x的范围”这一句中符号“f(x)”及“f(-x)”则应该判定为：同一个函数f(x)中的俩“函数值”。即同一个函数中“函数值f(x)”及“函数值f(-x)”。

　　同一个符号“f(x)”既可以表示“x的函数”，又可以表示“当自变量在定义域内取任意一个x值时，对应于该x值的 ‘对应函数值y ’”。

　　而符号“f(-x)”则纯粹是指同一个函数关系中的一个“函数值”，即同一个函数关系中，当自变量在定义域内取一对互为相反的数“x”、“-x”的值时，“-x”所对应的“函数值”就是“f(-x)”!

　　老王的这一观点在正统教科书中是可以找到依据的！下面出示教科书上的相关内容：

　　刘志斌不具有这基本的函数知识，所以将“f(-x)”误解为“有别于题设函数f(x)的另一个函数”。这就是刘志斌在明白数学的人们面前出的洋相！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　下面的截屏图片是刘志斌在229楼恶意的对老王正确观点进行诋毁和胡批的证据：

　　在同一个数学式子里，表达同一个函数关系得用同一个符号“f( )”；而在同一个式子里表达不同的函数关系就得用不同的函数关系符号，譬如用符号“φ( )”或“g( )”来与“f( )”相区别! 

　   刘志斌压根儿就不懂这样的基本知识，结果就把同一个不等式“(f(x)-f(-x))/x＜0”中的俩“函数值”符号误当成两个不同“函数关系”的“函数”了……