对数函数的定义域为{x│0＜x＜+∞}，在这样的单边型定义域里不存在“互为相反数”！

　　所以，对于函数f(x)=logax 怎么可能有“f(x)-f(-x)”之理呢？!

　　刘志斌不懂得这些基础知识，不懂也要装懂的在第2、3象限上画“x的对数函数”的曲线，真是贻笑大方！

　　针对楼下（303楼）多次重复打胡乱说的刘志斌：

　　刘志斌没有正确的函数基础知识，在自己先定义了“f( )”具体代表的“对应法则”为：“y等于x的对数”的前提下硬说同一坐标系中y轴左右两侧不同“对应法则”的曲线都可以标注相同的f( )记号。

　　经过300个帖的辩论，总算把夹着屎犟的刘志斌教明白了，于是刘志斌就恶意的把他在同一坐标系里对不是“y等于x的对数”这一“对应法则”的另两条曲线也标注相同‘f()’的错误隐匿起来啦！

　　大家看，刘志斌现在已经把同一坐标系内不同“对应法则”的曲线上误标的同一个记号“f()”删除啦！　

　　但是，刘志斌只删除曲线图中的“f()”也不能完全掩盖刘志斌的无知！大家可以看到表格图中的同一记号“f()”刘志斌却忘记了删，照样显露出刘志斌的无知！

　　刘志斌继续的打胡乱说：“1、如图，已知对数函数loga(x)　a＞1  x＞0，loga(1)=0，图像在1、4象限，增函数，2、那么对数函数loga(-x)   a＞1  (-x)＞0，所以x＜0，loga(-(-1))=loga(1)=0，图像应该在2、3象限，减函数，”

　　刘志斌虽然把他曲线图中的函数表达式f(x)=logax隐匿起来，只单拿其中局部的“对数式”loga(x)、loga(-x)来说事，企图掩盖他刘志斌的无知！但是，在刘志斌的函数列表的第1列里仍然还有忘记删除的函数表达式：f(x)=loga(x)；f(-x)=loga(-x)；以及f(-x)=loga(-x)对x轴的“镜像”曲线：-f(-x)=-loga(-x) !

　　刘志斌既已把“对应法则”记号f( )定义为“y等于x的对数”，怎么还允许自己在2、3象限画出“y等于x的对数”函数曲线来呢？！

　　刘志斌荒谬的以为在同一个表达式，或同一坐标系里换了颜色的f( )和f( )就不是同一个表示“y等于x的对数”的记号f( )了吗？！简直荒谬！！

　　不论你刘志斌换用什么颜色，在同一表达式或同一坐标系里，相同字母构成的法则记号f( )就只仅表示同一个“对应法则”，不可表示几个对应法则！

　　“y等于x的对数”函数的定义域是 x＞0，这个区域内的任何一个取值x的相反数‘-x’ 全都落在定义域之外啦！又哪来对应的“f(-x)” 和“-f(-x)”？！

　　刘志斌若想在y轴左侧表示另一个“对数”函数，那么它就不是“y等于x的对数”的对应法则啦！而是“y等于中间变量的对数”！应当用另一个记号，譬如用h(x)来表示，以示区别于已经赋予了“y等于x的对数”意义的“f( )”！

　　设：y是u的函数：y=g(u)=logau   (a＞1)，函数的对应法则为,“因变量y等于自变量u的对数"，定义域为u＞0 .

　　而u 又是x的函数：u=φ(x)= -x   (x＜0)  且φ(x)的值域使g(u)有定义，那么，y通过u的联系也是x的函数：y=h(x) .　我们就称 y=h(x)是由函数g(u)及φ(x)复合而成的函数，简称复合函数. 记作y=g[φ(x)]，其中的u（ 即φ(x) ）叫做“中间变量”。

　　刘志斌 不懂这些基础函数知识，不懂就不要装懂，不要在楼下(303楼)睁着眼说瞎话！……  

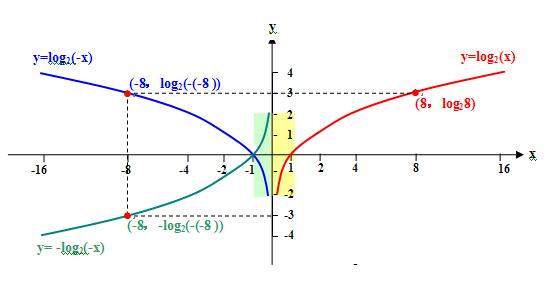
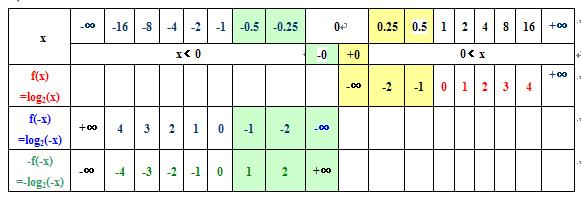
1、如图，已知对数函数loga(x)  a＞1  x＞0，loga(1)=0，图像在1、4象限，增函数，如图；2、那么对数函数loga(-x)  a＞1  (-x)＞0，所以x＜0，loga(-(-1))=loga(1)=0，图像应该在2、3象限，减函数，如图；

3、那么对数函数-loga(-x)  a＞1  (-x)＞0，所以x＜0，-loga(-(-1))= -loga(1)=0，图像应该在2、3象限，增函数，如图；

4、对于任意一个已知函数f(x)，都有与之相关的函数f(-x)存在，相关函数f(-x)图像与已知函数f(x)的图像以y轴为对称，所以有已知函数值f(x)=f(-x)相关函数值；

5、对于任意一个已知函数f(x)，都有与之相关的函数-f(-x)存在，相关函数-f(-x)图像与已知函数f(x)的图像以坐标原点为中心对称；所以有已知函数值-f(x)= -f(-x)相关函数值；

6、wanggq 不懂这些基础函数知识，不懂就不要装懂，不要睁着眼说瞎话！……    

　　这楼上，刘志斌再次的打胡乱说：“4、对于任意一个已知函数f(x)，都有与之相关的函数f(-x)存在，相关函数f(-x)图像与已知函数f(x)的图像以y轴为对称，所以有已知函数值f(x)=f(-x)相关函数值； 

　　5、对于任意一个已知函数f(x)，都有与之相关的函数-f(-x)存在，相关函数-f(-x)图像与已知函数f(x)的图像以坐标原点为中心对称；所以有已知函数值-f(x)= -f(-x)相关函数值；”

　　刘志斌的“打胡乱说”，暴露出刘志斌对函数基础知识的无知！

　　工业中应用的“温度自动记录仪”自动打印出的“温度－时间”曲线就是一个函数！可记作：f(t)   或者记作：f(x) .

　　对于这个函数f(t) 或者叫函数f(x)：其对应法则为“因变量T (或者y)等于测记时刻（即:因变量t 或x）所测记的温度值”，定义域为“从测温记录工作的启始时刻至记录工作终了时刻的期间”。

　　如图所示，我们根据这条已知的“温度­-时间”曲线f(x)就可以在直角坐标系上找到测温记录工作期间内任一时刻x所对应的被测物体的温度值T！譬如，我们过横坐标“5.5(小时)”的点引一垂线交温度曲线f(x)于点(5.5，f(5.5) )，再过点(5.5，f(5.5) )引一水平线交y轴即得纵坐标f(5.5)=39 (摄氏度) 。

　　对于这个已知的“测记温度T 是测记时刻t 的函数”T=f(t) 或者记为y=f(x)的函数来说，刘志斌是否也能搅出一个“f(-t)”或者“f(-x)”来？！而且满足所谓的“f(-t)=f(t)”，或者满足所谓的“f(-x)=f(x)” ？！

　　刘志斌是否也能搅出一个“-f(-t)”或者“-f(-x)”来？！而且满足所谓的“-f(-t)=-f(t)”，或者满足所谓的“-f(-x)=-f(x)” ？！

　　按照“刘志斌理论”把已知的f(x)的曲线绕y轴翻转，从而得到刘志斌所谓的f(-x)，是否根据这条f(-x)曲线就能追溯到测温记录工作启始时刻“0”之前5.5小时的时刻“-5.5(小时)”所对应的被测物温度？！

　　“刘志斌理论”上有“已知函数值f(x)=f(-x)相关函数值”，刘志斌应用这一理论是否能断定被测物体在时刻“-5.5(小时)”所对应的温度就等于在时刻“5.5(小时)”对应的39摄氏度？！

　　刘志斌无根无据，凭什么知晓：准备被测的物体在测记工作还未进行之前的某时段中任意时刻所对应的温度?！还有，刘志斌凭什么能让准备被测的物体在测记工作还未进行之前5.5(小时)的时刻“-5.5(小时)”对应的温度变为“零下39摄氏度”？！难道就凭你刘志斌有使函数曲线翻转的本事？！

　　很明显，由已知“温度-时间”函数f(x)经翻转得到刘志斌所谓的“f(-x)”和“-f(-x)”都是毫无意义的！而且还是荒谬透顶的！！

　　因而充分显露出这刘志斌的“4、对于任意一个已知函数f(x)，都有与之相关的函数f(-x)存在，相关函数f(-x)图像与已知函数f(x)的图像以y轴为对称，所以有已知函数值f(x)=f(-x)相关函数值；

　5、对于任意一个已知函数f(x)，都有与之相关的函数-f(-x)存在，相关函数-f(-x)图像与已知函数f(x)的图像以坐标原点为中心对称；所以有已知函数值-f(x)= -f(-x)相关函数值；”纯粹是无知者的一派胡言！！

　　老王把不等式“(f(x)-f(-x))/x＜0”中的符号“f(x)”及“f(-x)”解释为函数的自变量取一对互为相反数时分别对应的俩函数值，遭到刘志斌的恶毒诋毁。

　　所以，老王就引用高校教科书上的相关内容的照片资料来证明老王的解释是有根有据的。

　　下面的截屏图片就是老王的原贴内容：

　　刘志斌真是不要脸！恶意的将老王本来是用正统理论来作我们解题的正确“依据”的事实，诬蔑成：“堂而皇之的把它歪曲成‘错误和谎言’”！

　　到底是谁在打着“知识”的幌子堂而皇之的把正统大学教材中关于“函数自变量取互为相反的数值x，-x 所分别对应的函数值是f(x)和f(-x)”这一正确知识歪曲成“错误和谎言”的？正是他刘志斌自己！！

　　刘志斌对在同一式子里成对儿出现的“f(x)和f(-x)”是这样歪曲的：

『 11、任何情况下，f(x)、f(-x)是两个函数……12、任何情况下，f(x)、f(-x)都不是一个函数……13、任何情况下，f(x)、f(-x)都不是一个函数f(x)图像上的两个函数值；』

　　请看，这是刘志斌歪曲和诋毁该正确知识时所做的发言的截屏证据：

　　对老王把同一式子里成对儿出现的“f(x)和f(-x)”解释成函数自变量取互为相反的数值x、-x所分别对应的成对儿的“函数值”，刘志斌是这样诋毁的：

『5、由于wanggq和寒湘子，没有上述函数基础知识，对函数f(x)、f(-x)的关系乱作解释，给主楼题目解出了无数多个正确的解，所以无知是错误和谎言之源！！！或者说错误和谎言欺骗的是无知者！！！或者说无知是错误和谎言得以传播的动力 ！！！』

　　请大家看，这就是刘志斌诋毁老王和寒湘子正确解释“f(x)和f(-x)”意义时，所做的发言的截屏证据： 

　　请参见正统教科书上关于函数相关知识的论述：

　　f(x)是偶函数的标志是：当自变量x取一对互为相反的数的值时，函数的值不变，就是f(-x)=f(x) 。

　　这里很明显，等式f(-x)=f(x)中的“f(x)”表示当自变量的取值为“x”时对应的“函数值”；当自变量的取值为前者的相反的数值“-x”时对应的“函数值”则用“f(-x)”来表示！

　　事实上，正是他刘志斌自己打着“知识”的幌子诽谤和诋毁正统教科书上这部分内容！把这部分内容诋毁成“谎言”诋毁成“错误”!

　　当老王拿出教科书上的有关内容照片来证明：把同一式子里成对儿的f(x)、f(-x)解释成同一函数关系下，自变量取互为相反的数值所分别对应的成对儿的函数值有依有据时，刘志斌居然堂而皇之的倒打一耙，诬老王批教科书上这部分内容为谎言！刘志斌真是不要脸到了极点！

1、这又是一个高中数学题，看看人家是怎么做的？

　　网上的内容不足为凭！又不是正统的教科书内容！

　　网上说什么的都有，有正确的，也有错误的，刘志斌拿一个错误的东西当准绳岂不成大笑话！

　　在同一个表达式里出现的记号“f(x)”和“f(-x)”是表示同一个函数当自变量在定义域内分别取任意的一对互为相反的数值“x和-x”对应的一对“函数值”。

　　其理由是：f(x)和f(-x)两个记号所表示“对应法则”的记号是同一个字母f 来构成的“f( ) ”！所以，它们是同一个函数关系下成对儿的函数值！

　　函数y=logax 的“对应法则”是“y等于x的对数”，其定义域是x＞0 ，定义域内的任何一个取值x， 其相反数-x 全都落在定义域之外啦，所以，“y等于x的对数”函数的自变量不可能取得互为相反的数值！所以，函数f(x)=logax 中不存在“f(-x)” !

　　函数y=loga(-x) 的“对应法则” 是“y等于中间变量‘φ(x)=-x’ 的对数”，其中间变量“φ(x)=-x” 的定义域限为x＜0，定义域内的任何一个取值x，其相反数-x 全都落在定义域之外啦，所以，“y等于中间变量‘φ(x)=-x ’ 的对数”函数的自变量也不可能取得互为相反的数值！

　　y=logax 和 y=loga(-x) 这两个函数的对应法则显然是不同的！前者是“y等于x的对数”，后者是“y等于中间变量‘φ(x)=-x’ 的对数”。

　　在同一表达式或同一坐标系里，不允许用同一个记号“f( )”表示不同的“对应法则”！所以，对另一个法则“y等于中间变量‘φ(x)=-x’ 的对数”，我们得改用别的字母构成法则记号，譬如用h(x)区别于既已赋予“y等于x的对数”意义的f(x)!

　　同理，函数h(x)=loga(-x) 的自变量也不可能取得互为相反的数值！所以，对于函数h(x)也不存在所谓的“h(-x)”!　　

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　教科书告诉我们：“y是x的函数”记作 y=f(x)　也可以简记作 f(x) 。

　　在同时研究两个或多个函数时，要用不同的符号来表示它们，除f(x)外　还常用F(x)，G(x)，g(x) 等符号。

　　对于函数f(x)：

　1、如果对于定义域内的任何一个x，它的相反数-x也都在定义域内，且都有

f(-x)=-f(x)，则函数f(x)为奇函数。

　2、如果对于定义域内的任何一个x，它的相反数-x也都在定义域内，且都有

f(-x)=f(x)，则函数f(x)为偶函数。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 　

　　我们可以从中解读出：

　1、对于函数f(x)，只要有一个取值-x对应的f(-x)≠ -f(x)，则函数f(x)就不为奇函数！ 

　2、对于函数f(x)，只要有一个取值 -x对应的f(-x)≠ f(x)，则函数f(x)就不为偶函数！

　3、函数f(x)定义域内只要有一个取值x的相反数-x不在定义域内，则：不在定义域内的-x没有对应的“f(-x)” !  而函数f(x)则既不为奇函数，也不为偶函数！

　　请注意：成对儿出现的“f(x)”和“f(-x)”是同一个映射关系即同一个函数f(x)上自变量取互为相反的数值x和-x，分别对应的成对儿的“函数值”。 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　记号‘f(-x)’是人们研究讨论函数f(x)的奇偶性问题时引入的一个函数值记号，原本并不单独用来表示某个变化过程中的两个变量之间的映射关系—“函数”。

　　记号‘f(-x) ’只有与f(x)成对儿时才有它的意义。f(-x)括弧内的“-x”是表示自变量的某个取值，是相对于f(x)括弧内的取值x而言的相反数，并不是表示一个“量”。如果是表示“量”的话，只需一个字母即可，完全用不着给字母再添加负号！

　　关于原点对称的定义域，自变量的任意一个取值x都有相反数-x 。因为“相反”的意义即“互为相反”的意义，所以在对称的定义域内，自变量的每一个取值都可以是x或者-x的身份！　　

　　譬如：当取值x=-2 时，则相反的取值 -x=2；反过来，当取值x=2 时，则相反的取值-x=-2 。

　　如果你把“f(-x)”看成“函数”，那么，你实际上就是把“-x”原本的“数值”身份当作一个“量”来看待了！这个“量”即函数f(x)的自变量！在此前提下所谓的“函数f(-x)”，在本质上还是原函数f(x) !　　

　　函数实质上就是集合A到集合B的映射，对于自变量x在定义域A内的任何一个取值，在集合B中都有唯一的函数值y和它对应。

　　例如下面所示的两组映射：图2所示映射，原象集合A中的元素为图1所示映射原象集合A中元素的相反数。但是，图1图2分别所示的映射，完全是同一个映射！

　　我们改用“数据列表”的形式来表达函数f(x)=0.5x+2 ：

 　　再改用“图象”形式来表达函数 f(x)=0.5x+2 ：

　　在关于原点对称的定义域上，自变量取值x从小到大取遍每一个数值（x既可取负数，也可取正数），点P(x，f(x))在坐标平面留下的轨迹与自变量取相反数值-x从大到小取遍每一个数值（-x既可取正数，也可取负数），点Q(-x，f(-x))留下的轨迹完全是同一条曲线！以映射的观点来看，f(-x)与-x这两个“变量”之间的关系也叫“函数”！但是，这个所谓的“函数f(-x)”本质上还是原来的函数f(x) ! 

　　所以，讨论中仅用“f(x)”这一个记号就足以简单表示我们所讨论的“y=0.5x+2” 这一个函数啦！根本就用不着给表示“自变量”的字母x再添加个负号！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

　　先弄清楚什么叫做“关于y轴对称”、什么叫做“关于原点对称”、什么叫做“关于x轴对称”？！

　　大家都明白：

　　直角坐标系平面内任意一点P(x，y)，那么P关于y轴对称的点是点P'(-x，y) 。也就是说关于y轴对称的，成对儿的点的横坐标是‘互为相反的数’，纵坐标是‘相等的数’。

　 直角坐标系平面内任意一点P(x，y)，那么P关于原点对称的点是点P''(-x，-y) 。也就是说关于原点对称的，成对儿的点的横坐标及纵坐标都是‘互为相反的数’。

　　直角坐标系平面内任意一点P(x，y)，那么P关于x轴对称的点是点P'''(x，-y) 。也就是说关于x轴对称的，成对儿的点的横坐标是‘相等的数’，纵坐标是‘互为相反的数’。 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　在函数f(x)的图象上任取一点P(x，f(x))，那么P关于y轴的对称点是点P'(-x，f(x))。　如果：点P'(-x，f(x))也在f(x)的图象上，则：P'(-x，f(x))即为P'(-x，f(-x))。　即：f(-x)=f(x) !　也就是说，只有在f(-x)=f(x)的前提下才有“f(x)与f(-x)关于y轴对称”！

　　但是，如果f(-x)≠f(x)，则表明点P'(-x，f(x))并不在f(x)的曲线上  !   如下图所示函数f(x)=0.5x+2：f(-x)并不等于f(x)，即表明函数f(x)=0.5x+2曲线上的f(x)与f(-x)并不关于y轴对称！

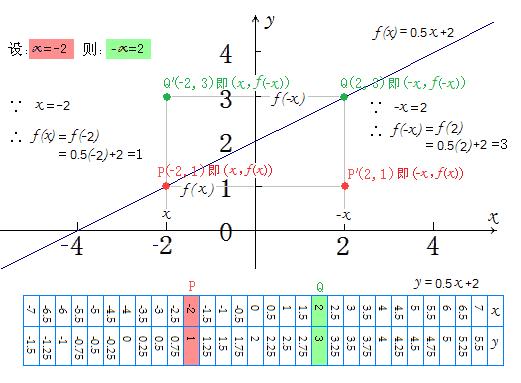
　　如果你抛开“f(-x)=f(x)”这一先决条件，而对f(-x)并不等于f(x)的情况妄下断言：“f(x)与f(-x)关于y轴对称”，就是错误的！

　　如果f(x)曲线上的点P(x，f(x))关于y轴的对称点P'(-x，f(x))在另一条（譬如）g(x)曲线上，那么，P'(-x，f(x))即为P'(-x，g(-x))。即：g(-x)=f(x) !　如果自变量取遍定义域内每一个数值，都有g(-x)=f(x)，则：f(x)与g(x)是关于y轴对称的两个不同映射关系的函数，其分别对应的两条曲线关于y轴相互对称！并不是“f(x)与f(-x)关于y轴对称”！ 

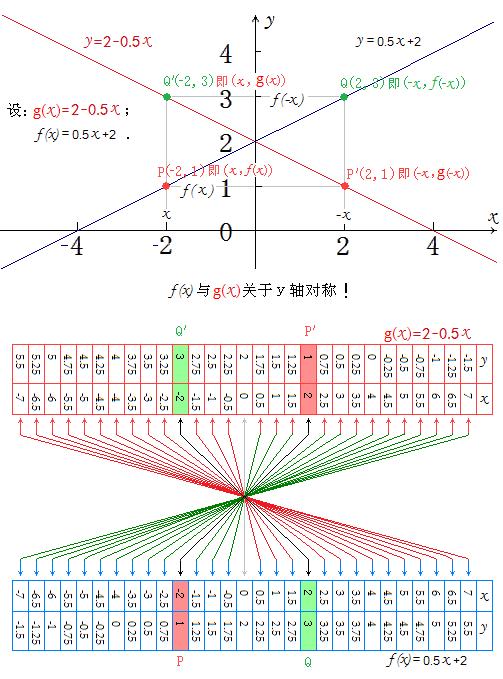
　　在同一式子或同一坐标系里，你要是象刘志斌那样用同一个“法则记号f( )”来表示两个不同的“对应法则”，那么，你就违背了教科书上关于“在同时研究两个或多个函数时，要用不同的记号来表示它们”的规定!  

　　在f(x)的图象上任取一点P(x，f(x))，那么P关于原点对称的点是点P''(-x，-f(x))。如果点P''(-x，-f(x))也在f(x)的图象上，则：P''(-x，-f(x))即为P''(-x，f(-x))。   即：f(-x)=-f(x) !　也就是说，只有在f(-x)=-f(x)的先决条件下才有“f(x)与f(-x)关于原点对称”！

　　请注意，当 f(-x)= -f(x)时，f(x)与-f(-x)却并不关于原点对称，而是关于y轴对称！　

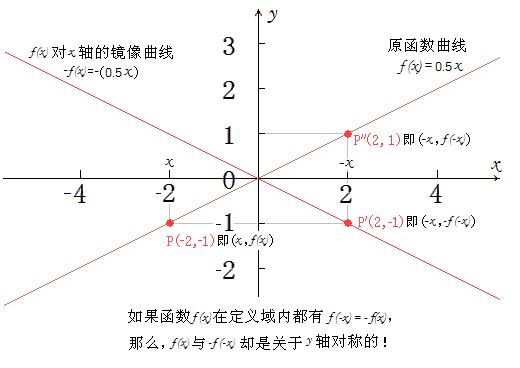
　　如果点P''(-x，-f(x))都不在函数f(x)的曲线上，而是都在另一条（譬如）h(x)曲线上，那么，P''(-x，-f(x))即为P''(-x，h(-x))。即都有：h(-x)=-f(x) ，则：f(x)与h(x)是关于原点对称的两个不同映射关系的函数，其分别对应的两条曲线关于原点相互对称！并不是“f(x)与-f(-x)关于原点对称”！ 

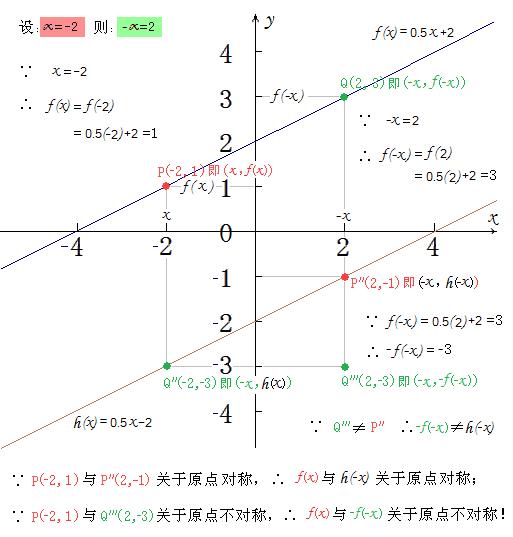
　　例如：设有函数f(x)=0.5x+2 若自变量取值x=-2，其相反取值-x则为2 .代入同一个法则“f( )”分别有函数值：

　　f(x)=f(-2)=0.5(-2)+2=1 　；　f(-x)=f(2)=0.5(2)+2=3  .

　　自变量取值x=-2时对应下图f(x)曲线上的点P(-2，1) ，则自变量相反的取值-x=2时对应f(x)曲线上的点Q(2，3) . 

　　显然，点P(-2，1)与点Q(2，3)并不是关于原点对称的！而点P关于原点对称的点是曲线h(x)上的点P''(2，-1) 即P''(-x，h(-x)) ! 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~　　　

　　函数f(x)图象上任意一点P(x，f(x))，那么P关于x轴的对称点是点P'''(x，-f(x))。

　　取遍函数f(x)图象上全部点关于x轴的对称点所连贯起来的曲线便是函数f(x)关于x轴的“镜像曲线”— -f(x) 。曲线f(x)与曲线-f(x) 是关于x轴对称的两条曲线。

　　设函数f(x)的定义域是关于原点对称的，如下图所示函数f(x)=0.5x+2图象上的点Q(-x，f(-x))其横坐标值-x是点P(x，f(x))横坐标值x的相反数。

　　图中任意的设自变量某一取值x=-2 ，则其相反的取值-x=2 . 把这一对互为相反的数值分别填入“f( )” 得：f(x)=f(-2)=1 ，f(-x)=f(2)=3 .  即：点P(x，f(x))坐标为(-2，1) ，点Q(-x，f(-x)坐标为(2，3) 。

　　点P(-2，1)即P(x，f(x))关于x轴对称的点是点P'''(-2，-1)即P'''(x，-f(x))，点Q(2，3)即Q(-x，f(-x))关于x轴对称的点是点Q'''(2，-3)即Q'''(-x，-f(-x))。

　　同理，当函数f(x)自变量取遍定义域内每一个数值x，则其相反的数值-x也被取遍了，把每一个“-x”分别所对应的点Q'''(-x，-f(-x))连贯起来形成的“曲线-f(-x)”，实质上仍然还是函数f(x)关于x轴的同一条“镜像曲线 -f(x)”！ 

引用 wanggq 的回复内容： 　　　

　这里很明显，等式f(-x)=f(x)中的“f(x)”表示当自变量的取值为“x”时对应的“函数值”；当自变量的取值为前者的相反的数值“-x”时对应的“函数值”则用“f(-x)”来表示！

1、这里的等式f(-x)=f(x)，是在描述偶函数以x轴为对称时出现的等式，等式f(-x)=f(x)中的“f(x)”、f(-x)表示当自变量的取值为“x”、“-x”时对应的“函数值”！

2、主楼的已知函数f(x)和要求的函数f(-x)是两个函数以x轴为对称的问题；

3、wanggq 读死书，认为只要是“f(x)”、f(-x)都是一个函数自变量的取值为“x”、“-x”时对应的“函数值，闹出了一个大笑话！

4、举例说：

5、上例的“f(x)”、f(-x)是两个函数以x轴为对称的问题，不再是一个函数上自变量x取相反数的两个函数值，

　　刘志斌的函数“知识”太二啦！偶函数的图象是以y轴为对称轴的！刘志斌却打胡乱说“偶函数以x轴为对称”！

　　别说是偶函数，就但凡为函数，其图象自身都绝不可能关于x轴对称！如果某条曲线是关于x轴对称的，那么该曲线就不能叫做“函数”！

　　譬如：以x轴为对称轴的抛物线，只有象刘志斌这种对函数基础知识不清楚的假冒伪劣“大师”才把它误当成“幂函数”！而合格的高中学生是绝不会将它误当成“函数”的！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　老王对不等式“(f(x)-f(-x))/x＜0 ”中f(x)、f(-x)的解释是：同一个函数当自变量在定义域内分别取任意的一对儿互为相反的数值“x和-x”时成对儿对应的“函数值”，自变量取值为x时，对应函数值f(x)，自变量取值为-x时，对应函数值f(-x)！

　　之前，刘志斌还一直夹着屎犟的打胡乱说：“11、任何情况下，f(x)、f(-x)是两个函数……12、任何情况下，f(x)、f(-x)都不是一个函数……13、任何情况下，f(x)、f(-x)都不是一个函数f(x)图像上的两个函数值；”

　　经过旷日持久的争辩，总算把刘志斌教来有点点儿醒悟了，稍有些知趣的放弃了自己之前坚称的：“任何情况下，f(x)、f(-x)都不是一个函数f(x)图像上的两个函数值”啦！不得不承认 f(x)、f(-x) 是同一函数关系下，自变量分别取一对互为相反的数值“x和-x” 所对应的成对儿的函数值！     

　　楼上这310楼刘志斌的“1、……等式f(-x)=f(x)中的‘f(x) ’、‘f(-x) ’表示当自变量的取值为‘x ’、‘-x ’ 时对应的‘函数值’ ”无异于刘志斌自己扇自己的嘴巴：看你刘志斌还屎犟“任何情况下，f(x)、f(-x)都不是一个函数f(x)图像上的两个函数值”不？！         

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　对应法则为“y等于x的对数”的函数f(x)，定义域是(x＞0)，它的自变量在定义域内的任意某取值x 其相反数-x 全都落在定义域之外啦，所以，它的自变量不可能取得互为相反的数！也就没有谈 f(-x) 的基础条件！因此无从谈起 (f(x)-f(-x))/x＜0 ！

　　刘志斌把 y=loga(x) 写成 f(x)=loga(x)，再把y=loga(-x) 写成 f(-x)=loga(-x)，并且把 f(-x)=loga(-x) 与 f(x)=loga(x) 放在同一式子或同一坐标系里就是明显错误的！

　　刘志斌由此错误基础上推导出来的刘志斌减法公式：“x＞0时，f(x)-f(-x)=f(x)

 及 x＜0时，f(x)-f(-x)=-f(-x) ” 都是刘志斌闹出来的大笑话!

 　　 f(x)=lgX 是“单边型定义域”的函数，定义域内任意一个x，其相反数-x都不在定义域内。所以f(x)=lgX 不允许有“f(-x)”！

　　刘志斌图中，y轴左侧曲线的对应法则“中间变量‘φ(x)=-x’ 的对数”与右侧曲线的对应法则“自变量的对数”是不同的。所以，左侧曲线对应法则的记号须得用另一个字母来构成，譬如用h(x)区别于右侧曲线上既已赋予“自变量的对数”意义的f(x) ！ 

　　同理，y轴左侧曲线“中间变量‘φ(x)=-x’  的对数”h(x)=lg(-x)也是“单边型定义域”的函数。同样不允许有“h(-x)”！

　　记号“f(-x)”得以存在的必要条件是：函数f(x)的定义域内有互为相反的数值x和-x共同存在！如果没有互为相反的数值x和-x共同存在于函数f(x)的定义域，那就必然不存在“f(-x)”！！

　　刘志斌不懂函数的基础知识，在解主楼的题目时对同一函数法则记号‘f( )’ 赋予不同‘对应法则’的意义。于是刘志斌就必然的要闹出笑话来！

　　笑话之一：对不等式‘(f(x)-f(-x))/x＜0 ’ 刘志斌赋予‘f(x)’的意义为“y等于自变量x的对数”在这一意义下使得‘f(-x)’无意义，从而不等式‘(f(x)-f(-x))/x＜0 ’ 也就无意义；反过来刘志斌赋予‘f(-x)’的意义是“y等于中间变量‘φ(x)=-x ’ 的对数”，在这一意义下又使得‘f(x)’无意义，从而不等式‘(f(x)-f(-x))/x＜0 ’ 同样无意义！套用刘志斌自己的话来说：刘志斌闹出的笑话“使楼主的题目变成了无知无解的错题”！

　　笑话之二：刘志斌把“f(x)”、f(-x)胡搅成“关于y轴成对称的曲线”，使得‘f(x)-f(-x)’恒等于0！即明显的不满足题目的“(f(x)-f(-x))/x＜0)”的要求！为了掩饰这一明显的错误，刘志斌再使劲的搅一搅：引入“代数和”的概念，f(x)减去f(-x)，等于f(x)加上“f(-x)的相反数-f(-x)” 。但是，众所周知：遵循“代数和”的法则去运算，其“代数和”仍然恒等于0！刘志斌咋个再搅下去呢？！

　　刘志斌立马偷换这“加上”一词的概念，把代数和所指的数值意义上的“加上”偷换为图形意义上的“拼合”！即：y轴右侧曲线f(x)与 y轴左侧f(-x)之镜像曲线‘-f(-x)’拼合起来，形成“关于原点对称的图形”，于是荒谬的刘志斌减法公式就出炉啦：“y轴左侧非f(x)=0，f(x)-f(-x)=-f(-x)；y轴右侧非f(-x)=0，f(x)-f(x)=f(x) ”  ！

　　刘志斌这样的胡搅，就如同3岁的“牛”宝贝儿把主持人的题目“8+1等于几？”解答成“8+1等于3” 一样的荒谬！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　CCTV 有一档《博乐先生微逗秀》节目上曾经的一个令人捧腹的桥段：

　　节目主持人逗3岁的“牛”宝贝儿：叔叔问你一个10以内加法的题，你会算吗？宝贝儿的头一扬：当然会算啦！

　　主持人问：8+1 等于几？

　　宝贝儿左手伸出姆指和食指做出代表数目“八”的手势，右手伸出食指做出代表数目“1”的手势，俩小手凑一块儿，用目光数了数俩手伸着的指头，答：等于3  !

　　主持人很诧异：8+1=9 嘛！你怎么算的，咋会等于3呢？！

　　“牛”宝贝儿不屑地反讥主持人：你不懂加法吗？这（左手代表八的手势）不是“8”吗，几个指头？两个嘛！加上这（右手伸出的）“1”不就是3个指头了吗？！！

　　看似宝贝儿很“牛”，实则宝贝儿无知！“牛”宝贝儿年幼，还不知道正确的思维应当遵循“同一律”！

　　刘志斌早已不年幼了，刘志斌的思维不遵循“同一律”是无知、还是恶意荼毒青年？！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 　　我们大家都应该尊重正统教科书上的理论！但是，刘志斌极端的自负，一贯藐视正统教科书中的理论！刘志斌读书时，根本就不用心去领悟正统教科书中理论的精髓，但凡刘志斌在知识上出现偏差和谬误时，刘志斌总是以自创的“刘理论”为“标准”去批判正统教科书上的理论！狂妄的自认为编写教科书的学者们都不如他刘志斌“牛”！

　　在刘志斌看来，所有参与工控论坛讨论的网友的观点都要以“刘志斌理论”为标准！如果有与“刘志斌理论”不同的观点，即便是从正统教科书上引用过来的观点也是“错误的观点”！

　　在辩论中，老王引用教科书上的正统理论为依据，提出与“刘志斌理论”不同的观点，刘志斌就竭力诋毁老王的观点是“死读书”得来的观点。

　　例如，正统教科书中的理论：

　　平面方程是关于x，y，z，的一次方程，反之，凡是关于x，y，z，的一次方程都表示一个平面。

　　设有一变量z，它与二变量x，y有这样的关系：二变量x，y在定义域内任意取定某一组值，变量z都有唯一确定的值与之对应，则称变量z为二变量x，y的函数，记作

　　　　　　　　　　　　　　　 z=f(x，y)  

　　当函数的自变量只有一个时，称为一元函数，当自变量为二个时，则称为二元函数。

　　下图是某高校的课件部分内容：

　　因为刘志斌对函数的“知识”与正统教科书上的理论相冲突，刘志斌不但不反省自己“知识”上的谬误，反而毫不尊重正统教科书上的理论，用自创的“刘志斌理论”对正统高校、正统教科书的理论一阵的胡批！

　　下面就是刘志斌对正统高校、正统教科书的理论进行胡批的截屏证据： 

　　刘志斌胡说八道的内容：

『1、函数 z=3x-2y，可以移项得 z-3x+2y=0；

　2、当z=0时，-3x+2y=0，是XOY平面坐标系的一条过原点的直线；

　3、当x=0时，z+2y=0，是ZOY平面坐标系的一条过原点的直线；

　4、当y=0时，z-3x=0，是XOZ平面坐标系的一条过原点的直线；

　5、x-3+2y=0，是一条空间直线；

　6、显然，这个高等学校的教材说函数 z=3x-2y是一个过原点的平面是错误的！』

　　刘志斌的这段胡批，真叫人笑掉大牙！

　　如果刘志斌认真读过教科书有关二元函数的内容，就应该知道：

二元函数 z=3x-2y 是过原点的一个平面！

　　如果刘志斌认真读过教科书有关平面方程的内容，就应该知道：

平面方程3x-2y-z=0是过原点的一个平面！

　　连高中学生都知道：三元一次方程 Ax+By+Cz+D=0 是平面的一般方程！可是，一贯把自己伪装成“大师”的刘志斌却不知道！这证明了刘志斌在这方面是无知的！

　　平面方程 3x-2y-z=0 可以写成一般形式：Ax+By+Cz+D=0 .　其中 A、B、C分别是仨未知数x、y、z的系数，D是常数项（本例：A=3，B= -2，C=-1，D=0 ）。

　　刘志斌写的方程“z-3x+2y=0” 实质上与平面方程  3x-2y-z=0 是同一个方程。

　　刘志斌的『5、z-3x+2y=0，是一条空间直线；6、显然，这个高等学校的教材说函数

 z=3x-2y是一个过原点的平面是错误的！』纯粹是刘志斌用他自己的无知来对正统高校教材进行诋毁的打胡乱说！

　　注意：空间直线可看作两平面的交线，所以，空间直线的一般方程是一个方程组：

｛A1x+B1y+C1z+D1=0，A2x+B2y+C2z+D2=0 ｝

　　老王当即指出：刘志斌所谓的那三条“直线”，是平面“z-3x+2y=0” 分别与坐标平面“XOY”，“ZOY”，“XOZ”相交的交线。难道刘志斌认为如果平面“z-3x+2y=0”与其它平面相交，那么平面“z-3x+2y=0”就不是平面了吗？！难道一个平面上因画有三条相交于一点的直线以后，该平面就不是平面了吗？！刘志斌的思维逻辑真是荒谬透顶！

　 那三条都过坐标原点的直线其中任意两条都可确定出过原点的同一平面“z-3x+2y=0” ! 

　　连初中学生都知道：相交两直线确定一个平面，这是很基础的几何知识。刘志斌咋就不知道这么基础的一点几何知识呢？

 　　老王的点拨让刘志斌有点点儿醒悟了，刘志斌赶紧的删掉这胡说八道的“5、x-3+2y=0，是一条空间直线；6、显然，这个高等学校的教材说函数 z=3x-2y是一个过原点的平面是错误的！”

　　但是，刘志斌仍然念念不忘用他自创的“刘志斌理论”对教科书的正统理论进行乱弹胡批！教科书说 z=f(x , y) 是二元函数，刘志斌就偏要说 z=f(x , y)是三元函数！



　　函数记号“z=f(x，y)” 表示：z是二变量(x、y)的函数。z又叫变化过程中的“因变量”，括弧内二变量x、y 是“自变量”，定义域D包含于平面XOY。这是常识！函数中的“自变量”和“因变量”是有区别意义的！

　　方程 3x-2y-z=0 中的 x、y、z 叫做方程的未知数，仨未知数相互之间是平等的、并列的关系！并不存在“因变量”与“自变量”之分！刘志斌却荒谬的试图对方程3x-2y-z=0 的x、y、z进行“谁是自变量，谁是因变量”的区分。这只是刘志斌的“胡搅”没有意义！ 

6、主楼题目已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题，与教科书描述一个偶函数以x轴为对称是两码事，wanggq张冠李戴了！

引用 wanggq 的回复内容：  　　网上的内容不足为凭！又不是正统的教科书内容！   

 别睁眼说瞎话了，只能是自己糟践自己！

　　刘志斌在312楼继续的打胡乱说：“6、主楼题目已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题，与教科书描述一个偶函数以x轴为对称是两码事”

　　你刘志斌哪一只眼睛看见过教科书描述“一个偶函数以x轴为对称”？！！别说是偶函数，就连但凡可以称作函数的任何一条曲线都不可能以x轴为对称轴！如果某条曲线是关于x轴对称的，那么该曲线就不能叫做“函数”！

　　譬如：以x轴为对称轴的抛物线，只有象刘志斌这种对函数基础知识不清楚的假冒伪劣“大师”才把它误当成“幂函数”！而合格的高中学生是绝不会将它误当成“函数”的！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 　　刘志斌别睁眼说瞎话了，你能具体指出哪一个“偶函数”是以x轴为对称的？！你刘志斌若指不出来还仍然睁眼说瞎话：“偶函数以x轴为对称”，只能是你刘志斌自己糟践自己！

　　你刘志斌知不知道什么叫做“以x轴为对称”？！哎！我们还是习惯按正统教科书上的说法：“关于x轴对称”！

　　设直角坐标系平面内任意一点p(x , y)，那么P关于x轴对称的点是点P'''(x , -y)　也就是说，关于x轴对称的、成对儿的点的横坐标是‘相等的数’，纵坐标是‘互为相反的数’。 

　　如果函数f(x)曲线上任意一点p(x , f(x))，那么P关于x轴对称的点是点P'''(x , -f(x))　注意，这一对儿“ f(x)”、“-f(x)” 是一对儿互为相反的数值。

　　我们都知道函数的定义：“如果对于x的每一个值，y都有唯一的值与它对应，那么就说x是自变量，y是x的函数。”

　　对于同一个自变量取值x，如果有一对儿互为相反的数值y和-y都与它对应，那就不符合函数的定义啦！所以，点P'''(x , -f(x))绝不可能在函数f(x)的曲线上！

　　如果一对儿关于x轴对称的点p(x , y)与P'''(x , -y)都在同一条曲线上 ，那么，这条曲线就不能叫做“函数”！

　　你刘志斌把那条横躺着的、开口向右的、关于x轴对称的抛物线误当做“幂函数”，那是你刘志斌对函数无知的表现！而合格的高中学生是绝不会把这样的一条抛物线误当做“函数”的！！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　 简单的说，成对儿的“关于x轴对称”的点的横坐标是相同的数值，纵坐标是相反的数值。如：P(x，y)跟P'''(x，-y)是“关于x轴对称”的点。

　　如果某曲线上任意一点P(x，y)，与其“关于x轴对称”的点P'''(x，-y)也都在该曲线上，则：该曲线是“关于x轴对称”的；

　　如果曲线A上任意一点P(xp，yp)“关于x轴对称”的点P'''(xp，-yp)都在曲线B上，反之曲线B上任意一点Q'''(xq，yq)“关于x轴对称”的点Q(xq，-yq)也都在曲线A上，则：曲线A跟曲线B是“关于x轴对称”的，曲线A、曲线B互为“关于x轴的镜像”。

　　如下图所示：函数f(x)=0.5x+2 的图象与其“关于x轴的镜像”是：-f(x)=-(0.5x+2)

　　刘志斌的“6、主楼题目已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题”纯粹是无知者的打胡乱说！

　　刘志斌起初是不论有没有“f(-x)=f(x)” 这个前提条件，笼而统之把所有的f(-x)都胡搅成与f(x)关于y轴对称。搅来搅去，现在又把题目搅成f(-x)与f(x)以x轴为对称的问题！刘志斌铆足劲的胡搅，把刘志斌自己的脑子也给搅混淆啦！！

　　教科书上有这样一个定理：若y=f(x)是定义在R上的任一函数，则有：

　　　　　　　①、F1(x)=f(x)+f(-x)是偶函数；

　　　　　　　②、F2(x)=f(x)-f(-x)是奇函数. 

　　我们运用该定理中的“f(x)-f(-x)是奇函数”这一断言，即可证明刘志斌的“6、主楼题目已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题”是错误的！是刘志斌在诡辩和瞎胡搅！！

　　证明：

　　设定义在R上的函数y=f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 ，其曲线如下图所示：

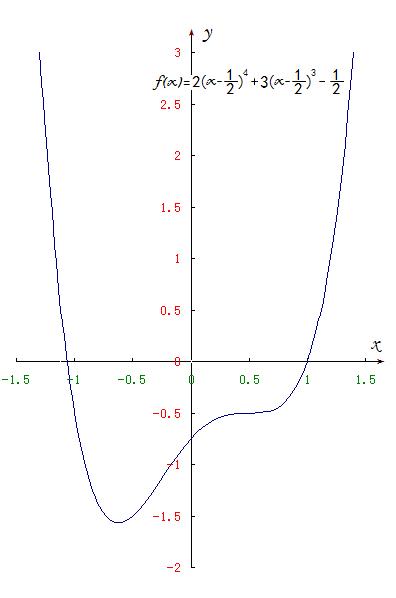
　　与这条f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5曲线关于x轴对称的另一条曲线(设为g(x) )就应该是：g(x)=-2(x-0.5)^4-3(x-0.5)^3+0.5 如下图红色曲线所示：

　　假设题目真如同刘志斌所谓的“已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题”，那么刘志斌所谓的“待求函数f(-x)”就如同上图中的g(x)曲线跟f(x)关于x轴对称的关系！这样，在这个例子中，g(x)等于刘志斌所谓的“待求函数f(-x)”！则：

　　f(x)-f(-x)=f(x)-g(x)

　　　　　 =2(x-0.5)^4+3(x-0.5)^3-0.5-[-2(x-0.5)^4-3(x-0.5)^3+0.5]

　　　　　 =2(x-0.5)^4+3(x-0.5)^3-0.5+2(x-0.5)^4+3(x-0.5)^3-0.5

　　　　　 =4(x-0.5)^4+6(x-0.5)^3-1　

　　其曲线如下图中的绿色曲线f(x)-g(x)所示：

　　函数f(x)减这个刘志斌所谓的与f(x)关于x轴对称的待求函数f(-x)，所得之差显然不符合“奇函数”的特征！这就证明了“与f(x)关于x轴对称的曲线”并不是“f(-x)” ! 

　　可见，刘志斌的“已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题”是无知者的打胡乱说！

　　其实很明显：

　　此例中的函数 g(x)=-2(x-0.5)^4-3(x-0.5)^3+0.5

　　　　　　　　　   =-[2(x-0.5)^4+3(x-0.5)^3-0.5] 不就是负的f(x)函数吗!

　　即：-f(x)才是跟f(x)关于x轴对称的，并不是如同刘志斌瞎掰的：“已知函数f(x)与待求函数f(-x)是两个函数以x轴为对称的问题”！

　　显然，刘志斌是把“-f(x)” 的性质张冠李戴的套到“f(-x)”头上去啦！ 

　　“f(-x)”是人们在研究讨论函数的奇偶性问题时引入的一个函数值记号。它表示：定义域内任意一对互为相反的数值x、-x 作自变量取值时，其中取值-x所对应的函数值。

　　函数奇偶性的定义：设X是一个对称数集，即对任意的x∈X，都有-x∈X，对于函数f(x)  ( x∈X ) ：

　　　　　　1、若恒有 f(-x)=-f(x)，则称函数f(x)是奇函数；

　　　　　　2、若恒有 f(-x)= f(x)，则称函数f(x)是偶函数。

　　由定义可知：

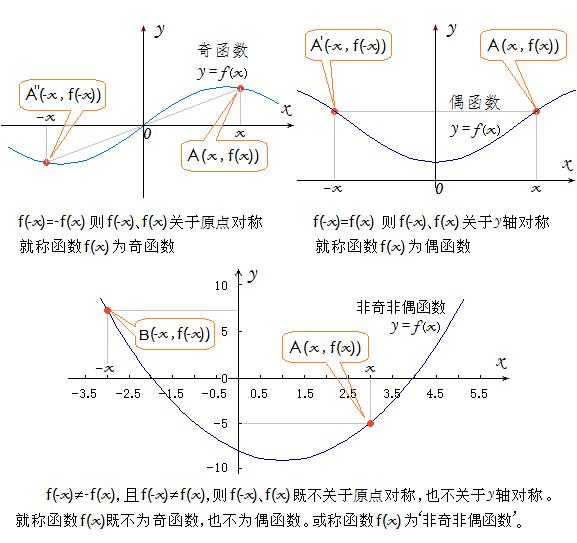
　　奇函数的图象关于原点对称，反之，图象关于原点对称的函数是奇函数；

　　偶函数的图象关于y轴对称，反之，图象关于y轴对称的函数是偶函数。

　　　f(x)=0 的图象是重合于x轴的一条直线，所以它既是奇函数，又是偶函数（同时具有奇、偶函数性质的函数仅此一例）。

 　　若 f(-x)≠-f(x) 且f(-x)≠f(x)，则函数f(x)既不是奇函数也不是偶函数。

　　于是，以奇偶性来划分，函数f(x) 可划分为以下四类：

　　　　　　1、是奇函数，但不是偶函数；

　　　　　　2、是偶函数，但不是奇函数；

　　　　　　3、既是奇函数，又是偶函数；

　　　　　　4、既不是奇函数，也不是偶函数。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　偶函数的图象是关于y轴对称的曲线，恒有f(-x)=f(x) 即 恒有f(x)-f(-x)=0，所以偶函数绝不可能满足(f(x)-f(-x))/x＜0。因此，主楼的题目绝不可选择偶函数来作解题用的函数f(x)！

　　因为题设“f(x)在0到正无穷大是增函数，f(1)=0”，说明该函数f(x)的 f(0)＜f(1)　即：f(0)＜0。而这 f(0)＜0，即说明对于主楼的题目也不能选择奇函数来作解题用的函数f(x)！

　　所以，对于主楼的题目，我们只能选择定义域内有互为相反的数值x、-x的“非奇非偶函数”来作解题用的函数f(x)！

　　譬如，我们可以选择这个“非奇非偶函数”：f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5  （定义域为：(-∞，+∞)）

　　 这是一个不折不扣的满足题目全部条件的f(x) !　　　　

　 求证：f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5   在0到正无穷大是增函数，且f(1)=0 

证明：

　把函数f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5展开, 并分解因式，得：

　　 f(x)=2x^4-x^3-1.5x^2+1.25x-0.75
　　　   =(x-1)(2x^3+x^2-0.5x+0.75)　
　　
　　显而易见，当x=1 时，f(x)=0 . 即 f(1)=0 .
　　
　　f(x)在(-∞，+∞)上连续，我们对f(x)求导：

　　f '(x)=8x^3-3x^2-3x+1.25
　　　    =(8x+5)(x-0.5)(x-0.5)

　　显而易见，导函数f '(x)=8x^3-3x^2-3x+1.25 的3个根：x1=-0.625、x2=0.5、x3=x2=0.5 .

　　如下图所示：

　　蓝曲线是f(x)=2x^4-x^3-1.5x^2+1.25x-0.75，红曲线是f '(x)=8x^3-3x^2-3x+1.25

　　在区间[0，0.5)内，8x+5＞0、 (x-0.5)^2＞0，所以f ’(x)＞0.
　　
　　在区间(0.5，+∞)内，8x+5＞0、 (x-0.5)^2＞0，所以f ’(x)＞0.

　　因此，函数f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 在[0，+∞)上是单调递增的。

　　即证明了函数f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 在0到正无穷大是增函数，f(1)=0。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

  　附录　　　由拉格朗日中值定理可以推导出判定函数单调性的法则：

　　设函数f(x)在[a ，b]上连续，在(a ，b)内可导.

　　(1) 如果在(a ，b)内f '(x)＞0 保持不变，那末，函数f(x)在[a ，b]上单调递增；

　　(2) 如果在(a ，b)内f '(x)＜0 保持不变，那末，函数f(x)在[a ，b]上单调递减。

　　如果把这个判定法中的闭区间换成其他各种区间（包括无穷区间），那末结论仍然成立。

<紧接下一楼的内容>

　　主楼题目核心“求(f(x)-f(-x))/x＜0时x的范围”是针对题设函数f(x)所提出的问题，这个不等式是对同一个函数在数值意义上的运算问题！其运算必须遵循代数运算的法则！

　　在同一个函数f(x)的前提下“求(f(x)-f(-x)) /x <0时x的范围”，其不等式中的“f(x)”及“f(-x)”表示自变量分别取互为相反的数值x和-x时，分别对应的成对儿的函数值。

　　求证：f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 在定义域( -∞，+∞)内有使(f(x)-f(-x))/x＜0的范围：

证明：

　∵　f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5

　　 　　=2x^4-x^3-1.5x^2+1.25x -0.75

　　保持该函数“对应法则f( )”不变，在定义域内用x的相反数“-x”去替换x 便得：

　　　f(-x)=2(-x)^4-(-x)^3-1.5(-x)^2+1.25(-x) -0.75 

　　 　 　=2x^4+x^3-1.5x^2-1.25x -0.75  

　∴　f(x)-f(-x)= 2x^4-x^3-1.5x^2+1.25x -0.75-[2x^4+x^3-1.5x^2-1.25x -0.75 ]

　　　　　  　= -2x^3+2.5x       

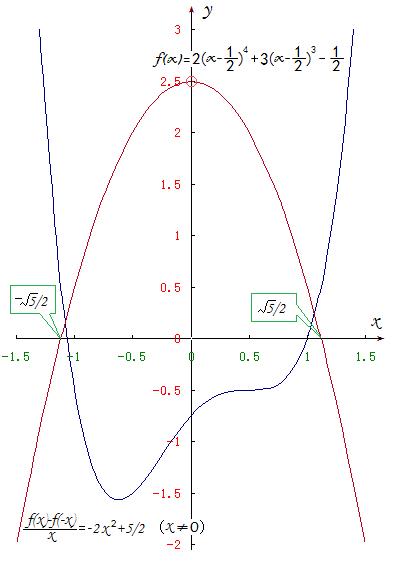
　∴　(f(x)-f(-x))/x=-2x^2+2.5    （x≠0）

　　解不等式 -2x^2+2.5＜0 　得：x＜-√5/2  或  x＞√5/2

　　所以，f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 在定义域( -∞，+∞)内有使(f(x)-f(-x))/x＜0的范围。　　　　　　  

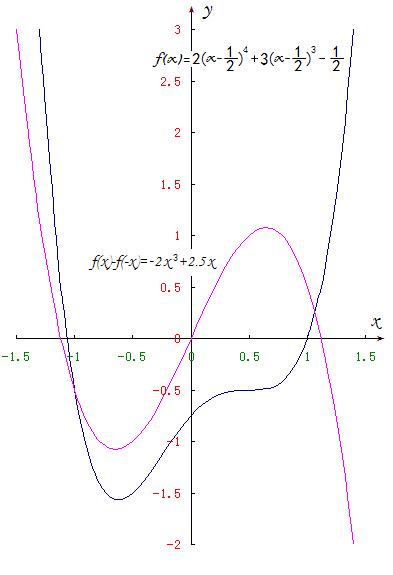
　　本例函数f(x)在(f(x)-f(-x))/x＜0时x的范围是：{ x＜-√5/2 } U { x＞√5/2 }

即：│x│＞√5/2

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 　　求(f(x)-f(-x)) /x <0时x的范围，这一不等式里的f(x)和f(-x)表示同一个映射关系(函数)下，自变量取互为相反的数值所分别对应的函数值。

　　我们在函数 f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5的定义域( -∞，+∞)内抽取一串关于0点对称的（自变量取值）数据以及它们分别所对应的（函数值）数据，并采用相反排序来构成图1和图2以示互为相反的数值x、-x分别对应的函数值y，因为集合是不论“排序”的，只要集合内的元素不增不减不更换，那便是同一个集合。

　　我们仔细对比图1和图2分别所示的映射，可以看出两组映射的原象集合是相同的数集，两组映射的象集合也是相同的数集。而且，只要两组映射的原象取相同的元素，则它们在各自的映射中的象总是相同的！因此，图1和图2分别所示的映射完全是同一映射 f : A→B ！即表明f(x)与f(-x)是同一映射关系下，互为相反的数值x与-x分别对应的象！也就是x与-x分别对应的函数值！

　　再换用函数表格来表明f(x)和f(-x)是同一函数关系下，自变量取互为相反的数值所分别对应的函数值：

　　上图中，水平连线箭头所指左右两侧函数表格的‘行’表示：同一函数f(x)的映射关系下，互为相反的自变量取值所分别对应的函数值f(x)与f(-x)；

　　对角连线箭头所指左右两侧函数表格的‘行’表示：同一自变量取值所对应的函数值是同一个y值，证明了连线左右两侧的函数表格都表达同一个函数f(x)。

　　我们再把函数表格转换成曲线图来表达同一式子或同一坐标系里的f(x)和f(-x)是同一映射关系即同一函数关系下，自变量在定义域内取互为相反的数值x、-x所分别对应的函数值！

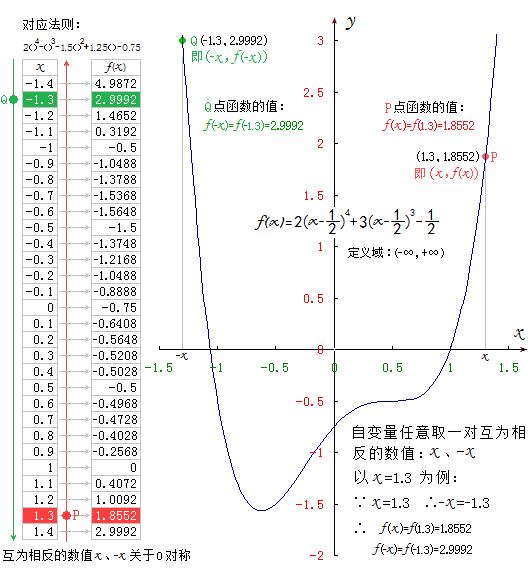
　　设函数f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5 曲线上有一动点P(x，f(x))和另一动点Q(-x，f(-x))，P、Q 两点的横坐标是互为相反的数值x、-x，即P、Q 是函数f(x)曲线上与y轴等距离的左右两点。请注意，函数曲线上与y轴等距离的左右两点并不一定就是“关于y轴对称的两点”！我们还须考察是否有f(-x)=f(x) ！  

　　直角坐标系平面上“关于y轴对称”的点必定满足“横坐标相反，纵坐标相同”缺一不可！

　　因为本例的f(-x)≠ -f(x)，且f(-x)≠ f(x)，所以函数f(x))=2(x-0.5)^4+3(x-0.5)^3-0.5 既不是奇函数，也不是偶函数！我们称这类函数为“非奇非偶函数”。

 　　在关于原点对称的定义域上，自变量取值x从大到小取遍每一个数值（x既可取正数，也可取负数），动点P(x，f(x))在坐标平面留下的轨迹与自变量取相反数值-x从小到大取遍每一个数值（-x既可取负数，也可取正数），动点Q(-x，f(-x))留下的轨迹完全是同一条曲线！这充分说明：

　　即便我们把动点Q的横坐标值-x看作“变量”，以映射的观点来看，f(-x)与-x这两个“变量”之间的映射关系也叫“函数”！但是，这个所谓的“函数f(-x)”本质上还是原来的函数f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5  ! 简单表示这个函数时，仅用记号f(x) 即可，并不需要再给表示自变量名的字母x添加一个负号“-”！所以，记号f(-x)仅用于表示同一个函数关系下，当自变量取互为相反的数值x、-x时其中-x所对应的函数值！

　　教科书上说“函数是增函数还是减函数，是对定义域内某个区间而言的。有的函数在一些区间上是增函数，而在另一些区间上是减函数。” 

　　譬如函数f(x)=x^2在0到正无穷大（即[0，+∞)区间上）是增函数，在(-∞，0)区间上是减函数。

　　我们不能象刘志斌那样因为f(x)=x^2在0到正无穷大是增函数，就咬定f(x)=x^2的定义域是半开区间[0，+∞)、更或者咬定f(x)=x^2的定义域是开区间(0，+∞)！大家都知道：函数f(x)=x^2 的定义域是(-∞，+∞) ！！

　　刘志斌一贯的藐视正统教科书上的理论！所以刘志斌不屑于用心来读书！所以才导致刘志斌对题目的理解完全背离正统教科书上的理论！

　　刘志斌荒谬的认为，题目设“f(x)在0到正无穷大是增函数，f(1)=0”那么所设函数f(x)的定义域就必定是“在0到+∞  ”。这只能说明刘志斌搞不懂函数的“单调区间”和“定义域”这两个不同概念之间的联系和区别！　

　　题目核心“求(f(x)-f(-x))/x＜0时x的范围”其中一对记号“f(x)、f(-x)” 分明是同一映射关系下，定义域内任意一对儿互为相反的数值所分别对应的成对儿的函数值。请参见数学教科书相关的理论！

　　刘志斌不懂装懂，还非得叫参与争论的网友必须以他的“刘志斌理论”为准！非得要大家都把该“不等式(f(x)-f(-x))/x＜0”里的一对记号“f(x)、f(-x)” 误当做“关于y轴对称的两个函数”！

　　设X是一个对称数集，即对任意的x∈X，都有-x∈X 。若这个数集X包含于函数 f(x)的定义域，则函数f(x)的值域中有成对儿的函数值f(x)和f(-x)。

　　奇函数、偶函数的定义域都是对称的数集：

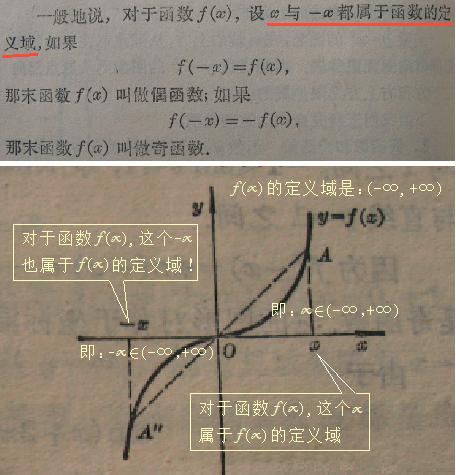
　　对数函数f(x)=logaX 虽然也是属于“非奇非偶函数”，但是，它的定义域{x│x＞0 }却不满足“有互为相反的数值x、-x同属于集合X”。所以它不能使“(f(x)-f(-x))/x＜0”有意义！

　　刘志斌选择“x的对数”函数f(x)=logaX来解主楼的这道题，是明显错误的选择！

　　首先，函数f(x)=logaX 的定义域(0，+∞)内不存在互为相反的数值x、-x ，所以，“x的对数”函数f(x)不存在“-x”所对应的函数值“f(-x)” ！使得“f(x)-f(-x)”失去意义！也就使得不等式“(f(x)-f(-x))/x＜0”失去意义！

　　其次，“x的对数”函数f(x)=logaX 定义域内不存在数值0，所以不存在0所对应的对数函数值f(0) ！也就无从谈及x＞0的函数值f(x)与不存在的f(0)进行大小的比较！即不能百分之百符合题设“在0到正无穷大是增函数”的这一条件！粗略只能算是打了折扣的“擦边球”式的“符合”。

　　<烟雨朦朦>早就指出过：当x＞0时，对于刘志斌的“f(-x)”没有意义，所以使得　 f(x)-f(-x)失去意义！当x＜0时，f(x)=logaX 又失去意义，所以也使得f(x)-f(-x)失去意义！ 

　　套用刘志斌自己的话来说，因为刘志斌无知的胡搅“使楼主的题目变成了一道无知无解的错题”！

　　在争论中，刘志斌也曾经删改了这一对儿曲线上标注的“f(x)=logaX” 和“f(-x)=loga(-x)”，经过删改后，一对儿曲线上只分别留下“f(x)”和“f(-x)”。下面就是刘志斌删改之后的截屏图片：

　　但是，刘志斌却没有注意他的文字仍然有“f(x)=logaX；f(-x)=loga(-x)”这样的描述！

　　同一式子或同一坐标系里，同一个法则记号“f( )”,仅只表示同一个“对应法则”。刘志斌不知道这些基础知识，错误的将两个不同的“对应法则”用同一个记号“f( )”来表示！

　　假如刘志斌的这对儿曲线不表示“x的对数”，而是改为表示：“x绝对值的对数”，则：定义域为 {x│x∈R  且x≠0 } ，该定义域是对称的数集（只有对称的定义域(亦或定义域内的某区间)才会有互为相反的数值x、-x）！从而这对儿曲线上才会有互为相反的x和-x分别对应的函数值“f(x)”和“f(-x)”。 

　　即便改为这样，可以使“f(x)-f(-x)”有意义，但是，但凡这种关于y轴对称的函数（即偶函数）也不可能使题目的不等式“(f(x)-f(-x))/x＜0”有获得成立的范围!  

　　因为偶函数的特征是 f(-x)=f(x) ，所以对于偶函数，恒有f(x)-f(-x)=0 。也就是说，关于y轴对称的函数，其f(x)-f(-x)绝不可能小于0 或大于0！　　 

　　即：关于y轴对称的函数，在x≠0时，其“f(x)-f(-x)”的值是绝不可能与自变量的值x异号的！