引用 寒湘子 的回复内容：

 谎言多了，也就分不出真假了。假作真时真亦假！ 

1、1楼的发言不是谎言，只是理解错了，说错了；

2、378楼的发言是谎言；

3、谎言总可以分辨；

4、只有撒谎的人，以为谎言难辨；

5、谎言总归是谎言，谎言难过“时间关 ”！

　　f(x)曲线上位于y轴左右两边等距离的点只有满足“左边点的纵坐标大于右边点的纵坐标”这一必要条件，才会使(f(x)-f(-x))/x＜0！

　　在x＜0时，f(x)曲线上位于y轴左右两边等距离的点的纵坐标分别对应为f(x)和f(-x)。若左侧f(x)大于右侧f(-x)，则f(x)-f(-x)＞0，与小于0的x异号，即(f(x)-f(-x))/x＜0；

　　在x＞0时，f(x)曲线上位于y轴左右两边等距离的点的纵坐标分别对应为f(-x)和f(x)。若左侧f(-x)大于右侧f(x)，则f(x)-f(-x)＜0，与大于0的x异号，即(f(x)-f(-x))/x＜0；

　　刘志斌连这么简单的道理都懂不起，还敢愣充“大师”！

　　刘志斌把位于y轴右侧的曲线复制翻转到左侧，形成‘关于y轴对称’的曲线是根本不可能得到(f(x)-f(-x))/x＜0的！

　　设函数f(x)的定义域包含‘关于0点对称的x和-x’，其自变量取互为相反的数值x、-x，分别对应“函数值f(x)”、“函数值f(-x)”。即当自变量取值为“x”时，对应的函数值为“f(x)”；当自变量取值为前者的相反数“-x”时，对应的函数值为“f(-x)”。

　　譬如说，函数f(x)=3x-1 ，对于该函数，当自变量取值为“5”时，其函数值为f(5)=3*(5)-1=14 ；而自变量取值为“5的相反数”即“-5”时，其函数值为f(-5)=3*(-5)-1= -16  。

　　刘志斌连这么简单的道理都弄不懂，还好意思愣充什么“大师”！刘志斌以“知识”的名义歪曲和诋毁正统教育机构编写的教材内容！并以荒谬的“刘志斌理论”荼毒青年！这不是罪恶又是什么？！！ 

  　　老王是通过逻辑推理得出的结论：函数曲线上位于y轴两侧等距离的点的纵坐标即成对儿的f(x)、f(-x) 只有满足“左边点的纵坐标大于右边点的纵坐标”这一必要条件，才会得到(f(x)-f(-x))/x＜0！

　　要说“编造”，一惯把自己伪装成“大师”的刘志斌，才是一贯无根无据的编造荒谬的“刘志斌理论”！大家看，这就是刘志斌胡乱编造出来的：

  　　　『 2）左边点的纵坐标小于右边点的纵坐标；

　 　　　 　  3）左边点的纵坐标等于右边点的纵坐标； 

　　　　   　 4）……                                                』

　　难道刘志斌以为“左边点小于右边点的纵坐标”也可以使对应的(f(x)-f(-x))/x＜0吗？！

　　难道刘志斌以为“左边点等于右边点的纵坐标”也可以使对应的(f(x)-f(-x))/x＜0吗？！

　　告诉你刘志斌，“左边点小于右边点的纵坐标”必然使对应的(f(x)-f(-x))/x＞0 ！

　　在x＜0时，f(x)曲线上位于y轴左右两边等距离的点的纵坐标分别对应为f(x)和f(-x)。若左侧f(x)小于右侧f(-x)，则f(x)-f(-x)＜0，与小于0的x同号，即(f(x)-f(-x))/x＞0；

　　在x＞0时，f(x)曲线上位于y轴左右两边等距离的点的纵坐标分别对应为f(-x)和f(x)。若左侧f(-x)小于右侧f(x)，则f(x)-f(-x)＞0，与大于0的x同号，即(f(x)-f(-x))/x＞0。

　　例如：函数f(x)=e^x-e 在R上是增函数，在0到正无穷大（即在[0, +∞)上）当然也是增函数！因为半开区间[0, +∞)包含于R嘛！而且，当x=1时，f(1)=e-e=0  所以，完全符合题设的“f(x)在0到正无穷大是增函数，f(1)=0 ”。

　　因为f(x)的定义域R包含(-∞,+∞)开区间，包含着‘关于0点对称的x和-x’，所以，此函数f(x)在x大于0的范围和x小于0的范围都能使“(f(x)-f(-x))/x ”有意义！

　　但是，此函数f(x)的曲线上位于y轴两侧等距离的点，左侧点的纵坐标小于右侧点的纵坐标，必然使“f(x)-f(-x)”与“x”同号（参见下图中红色曲线φ(x)=f(x)-f(-x)），故“(f(x)-f(-x))/x”大于0 （参见下图中绿色曲线h(x)=(f(x)-f(-x))/x）！从而不能符合题目核心“求(f(x)-f(-x))/x＜0时x的范围”的题意要求。

　　因此，选择在定义域全域内单调递增的函数来解这个题目，也是一种错误！

　　告诉你刘志斌，“左边点等于右边点的纵坐标”必然使对应的(f(x)-f(-x))/x=0 ！不论分处于y轴左右两边等距离的点的纵坐标对应f(x)或对应f(-x)，因为f(x)等于f(-x)，所以总是 f(x)-f(-x)=0，故总是 (f(x)-f(-x))/x=0    (x≠0)。

　　又例如：函数f(x)等于“自变量平方的4次方根减去1”也完全符合题设的“f(x)在0到正无穷大是增函数，f(1)=0 ”。且在x大于0的范围和x小于0的范围也都能使“(f(x)-f(-x))/x ”有意义！

　　但是，由于此函数f(x)的曲线上位于y轴两侧等距离的点的纵坐标总是相等的，所以，必然使“f(x)-f(-x)”恒等于0，故“(f(x)-f(-x))/x”恒等于0 ！（x≠0）从而不能符合题目核心“求(f(x)-f(-x))/x＜0时x的范围”的题意要求。　

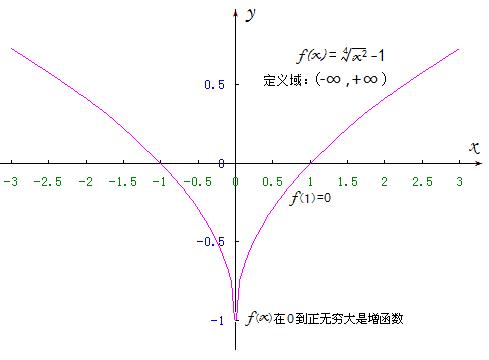
　　设：此图所示函数f(x)曲线上的f(x)-f(-x) 记作：φ(x)；而(f(x)-f(-x))/x 记作：h(x) .

则：φ(x)的对应法则为 y=0  （常值函数）；h(x)的对应法则为 y=0  (x≠0)  （常值函数）。

　　φ(x)的图象是重合于x轴的直线；h(x)的图象也是重合于x轴的直线，但在x=0处，h(x)没有定义，故x=0处h(x)没有图象。为了表示这一意思，h(x)重合于x轴的直线在坐标原点处要画一空心的小圆点（圈）。

　　由此可见，选择关于y轴对称的曲线所对应的函数f(x)来解这个题目，也是一种错误！　

　　函数曲线在y轴左右两侧等距离的俩点的纵坐标“f(x)与f(-x)”之间比较大小的结果不外乎是“大于、小于、等于”这3种可能。

　　可刘志斌却居然还要无中生有的编造第4种可能：『4）…… 』！大家看，刘志斌的这第4条连具体“内容”都无法陈述出来，也要胡乱的抓一“……”符号来充作个条款！多么卑鄙可笑的“刘志斌条文”！ 

　　刘志斌少见多怪地打胡乱说：『3、一个题目有无数个正确的解，那肯定是错误的！』这也不足为奇！

　　在数学基础知识方面，刘志斌本来就知识面不够宽，要让这位假冒伪劣的 “大师”刘志斌去理解有些题目的正确答案不不止1个（即结果不具唯一性），确实是难为他刘志斌啦！

　　请看，CCTV《少年中国强》节目给10岁少年何布凡出的考试题目《由循环小数倒推为“整数÷另一个整数”的商》这是个外延很大的题目，因为题目没有具体指出哪一个循环小数，那就得由你任选！不论你选的是纯循环小数还是混循环小数，只要你选的是从小数点以后某一位起，循环不止的出现某个或某些数字的这种小数都行！都符合题意！

　　例如：由纯循环小数0.123123……倒推为“整数÷另一个整数”的商；

　　　　　由混循环小数0.8123123……倒推为“整数÷另一个整数”的商.

　　即便选定了某个具体的循环小数，由于题目只是说由它倒推为“整数÷另一个整数”的商，并没有说由它倒推为“既约分数”。所以，其答案结果也不具唯一性！

　　这种题目的特点就是：结果不具唯一性！下面是电视屏幕的截屏图片：

　　因恐有人怀疑考试作弊，为了避嫌，主持人随机抽选台下自告奋勇的观众为何布凡同学随意选择循环小数。

　　例如：何炅随意选择的纯循环小数0.317317…… （循环节是317）；

　　　　　观众随意选择的混循环小数0.823462346…… （循环节是2346）.

　　何布凡同学以他超人的心算能力，一口气接连倒推出10多个正确的答案！节目是有时间限制的，有这10多个正确答案已经足以展示小布凡的超强心算能力！适可而止，无需将海量的正确答案全都列举出来！所以，评委老师童哲（大学校长）郑重的宣布：“到目前为止，何布凡同学倒推出的所有答案全都是正确的！”

　　下面就是何布凡同学倒推出的一批答案中的部分答案：（从电视屏幕截屏图片上剪裁的一部分答案）

　　你刘志斌既然认为“一个题目有无数个正确的解，那肯定是错误的！”那末，就请使出你愣充“大师”的本事来推翻何布凡同学心算出来的这些答案吧！！

　　事实上，愣充“大师”的刘志斌要推翻小学五年级学生何布凡心算出的这些正确的答案中的任何一个，那都是绝不可能的，那都犹如蚍蜉撼大树，不自量力！

　　同理，“f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x＜0时x的范围”同样是答案不具唯一性的题目！因为题目并没有明确的指定题设f(x)所代表的变量x和y之间具体的函数关系以及函数的定义域！那就得由解题的同学们自主选择！只要你选择的函数f(x)既符合题设条件“f(x)在0到正无穷大是增函数，f(1)=0”，又能使其曲线上有“(f(x)-f(-x))/x＜0 ”的范围，那就符合楼主所给题目的全部题意要求了。

　　符合题设条件“f(x)在0到正无穷大是增函数，f(1)=0 ”的函数是无穷无尽的！但符合题目核心之题意的f(x)却偏巧不能是刘志斌猜想的『f(x)=logax  a＞1』！

　　刘志斌自认为符合题意的f(x)只能选择『f(x)=logax  a＞1』、<烟雨朦朦>认为可以自主选择 f(x)=lxl-1 、f(x)=x^0.5-1、寒湘子认为可以自主选择 f(x)=x-1 、f(x)=e^x-e  等等……。刘、烟、寒这哥儿仨都不认为自己选择的函数f(x)叫做『给题目补充了条件』！那末，老王当然也可以自主选择 f(x)=3x^4-8x^3+6x^2-1 、自主选择 f(x)=2-4/(x+1) 等等，当然也不应该被这哥儿仨给误叫做『给题目补充了条件』！

　　解题者自主选择的各个函数f(x)，因为其f( )代表的具体“对应法则”不同，就可能造成函数f(x)曲线上其(f(x)-f(-x))/x＜0时x的范围有所不同！

　　选择f(x)=3x^4-8x^3+6x^2-1 时，其(f(x)-f(-x))/x = -16x^2  (x≠0)  所以，正确答案是：(f(x)-f(-x))/x＜0时x的范围为 除0之外的一切实数。

　　选择f(x)=2-4/(x+1) 时，其(f(x)-f(-x))/x =8/(1-x^2)     (x≠±1, x≠0)  所以，正确答案是：(f(x)-f(-x))/x＜0时x的范围为 (-∞，-1)∪(1，+∞) 即 除闭区间[-1，1] 之外的一切实数。

　　你刘志斌既然认为“一个题目有无数个正确的解，那肯定是错误的！”那末，就请使出你愣充“大师”的本事来推翻老王的这两个正确答案吧！！

　　同样的，愣充“大师”的刘志斌妄图推翻老王的这两个正确答案，那末刘志斌的图谋就犹如这蚍蜉撼大树，不自量力！

　　刘志斌在17楼也已经承认对于单边型定义域的函数f(x)来说，f(x)-f(-x)的减数和被减数总有一个不存在：

　　但是，刘志斌仍然坚持瞎胡搅：『当x＞0时，-f(-x)不存在，所以f(x)-f(-x)就是f(x)：当x＜0时f(x)不存在，所以f(x)-f(-x)就是-f(-x) 』.          　

　　刘志斌拒不认错，仍然多次的重复着他那荒谬的“刘志斌乱弹理论”，妄图以千遍百遍的“重复谬误”来让年轻的刘粉丝们分辨不清正确与谬误！以便他把荒谬的“刘志斌乱弹理论”伪装为“经典”来荼毒青年！

   　　№374楼刘志斌再次重复的歪曲题意，否认符合全部题意的函数之定义域必须包含“关于0点对称的区间”，把题目核心“求(f(x)-f(-x))/x＜0时x的范围”其不等式左边分子中的f(x)-f(-x)原本是在同一个函数定义域内施行的 “数值运算意义”上的f(x)减去f(-x)（或 f(x)加上-f(-x)）运算概念给偷换为对分居于y轴左右两侧的其定义域没有交集的俩函数图象施行“图形拼合”的概念即刘志斌乱弹为：“f(x)叠加-f(-x)” 的所谓“运算”！从而胡搅出荒谬透顶的“刘志斌运算”之解：

　　『-1＜x＜0　f(x)-f(-x))/x=-f(-x)/x＜0 　　0＜x＜1  f(x)-f(-x)/x=f(x)/x＜0 』！

　　函数y=log2(x) 是“单边型定义域”的函数，刘志斌在对应表格中将其标注为：f(x)=log2(x)，其定义域为(0,+∞) ，所以，在其定义域(0,+∞)内任意取一个数值x时，其相反的数值“-x”都不在其定义域(0,+∞)内！因而对于函数y=log2(x)来说，是不存在f(-x)的！那末，因f(-x)的“不存在”而必然使得f(x)-f(-x)的运算无意义！无意义的运算就必然无解！

　　请网友们注意：对于f(x)=log2(x)来说，刘志斌自己也承认当x＞0时，f(-x)不存在、f(-x)无图象，并不是f(-x)=0 !  但在这样的前提下，刘志斌却荒谬的自创“理论”规定：『 在x＞0时，f(x)-f(-x)=f(x) 』，进而荒谬的“运算”出这种根本不能成立的乱弹之“解”来：『 0＜x＜1  f(x)-f(-x)/x=f(x)/x＜0 』！

　　多么荒谬的＂运算＂！多么荒谬的乱弹之＂解＂！

　　请网友们注意：

　　记号“f(-x)”不是单独用来简单表示“因变量y是自变量x的函数”这一意涵的！这是因为：自变量的表示，仅仅只用一个字母足矣！根本就用不着再给字母添加一个“负号”！

　　记号“f(-x)”只有与记号“f(x)”配对使用才有意义，其意义是：同一个“函数对应法则f( )”下，在定义域内自变量取任意一对儿互为相反的数值（x和-x）时，数值“-x”所对应的函数值“f(-x)”。f(-x)括弧内的“-x”仅只表示相对于另一个函数值“f(x)”括弧内的“x”而言的相反数而已！并不是如刘志斌胡搅的“对相反数-x自身再次取反”的法则！

　　既然刘志斌先将f(x)定义为y=log2(x) ，那末，在同一表格和同一算式中对于另一对应法则的函数y=log2(-x)来说，刘志斌就不该再用同一个法则记号“f( )”不加区分的表示它！

　　在同一坐标系或同一算式中表达不同对应法则的函数时，必须用不同的表示法则的记号来加以区分！譬如用“g( )”区别于“f( )”。

　　譬如在同一坐标系或同一算式中，用记号“f(x)” 表示：y=log2(x)   x＞0，而用另一个记号“g(x)”表示：y=log2(-x)   x＜0 。

　　这里的f(x)其定义域是(0,+∞)，而g(x)的定义域却是(-∞, 0)，二者没有“交集”，或者说f(x)=log2(x)与g(x)=log2(-x)没有“公共的定义区域”。众所周知：不在公共定义区域上的俩函数相互运算是没有意义的！

　　当x＞0时，f(x)有定义，但g(x)没有定义；翻转过来，当x＜0时，g(x)有定义，但f(x)却又没有定义！从而在一切实数范围内使f(x)-g(x)的减数和被减数中至少总有一个不存在！即f(x)-g(x)在一切实数范围内的运算全都是没有意义的!

　　刘志斌不懂得函数的这些基础知识，胡乱的将处于同一不等式“(f(x)-f(-x))/x＜0”中表示“同一对应法则下，自变量取任意一对儿互为相反的数值x和-x所分别对应的一对儿函数值”的俩记号f(x)和f(-x)胡乱解读为“两个不同对应法则的y=log2(x)和y=log2(-x)”。

　　所以，刘志斌意识里的“f(x)-f(-x)”就相当于上述的“f(x)-g(x)”。即便依从刘志斌自己的定义，那末，在x∈(-∞,0)时，f(-x)=log2(-x)有定义，但f(x)=log2(x)没有定义；翻转过来，在x∈(0,+∞)时，f(x)=log2(x)有定义，但f(-x)=log2(-x)却又没有意义！从而在一切实数范围内都使f(x)-f(-x)=log2(x)-log2(-x)的运算完全没有意义！

　　既然f(x)-f(-x)=log2(x)-log2(-x)在一切实数范围内的运算全都是没有意义的，那末，刘志斌的乱弹之“解”：『-1＜x＜0　f(x)-f(-x))/x=-f(-x)/x＜0 ；0＜x＜1  f(x)-f(-x)/x=f(x)/x＜0 』就纯粹是无知者的打胡乱说！

老王，你和老刘吵架，我不想管，也管不了。

这个题目最先是我回应的。我认为题目出得有问题。可人家刘老师一开始就拿一个对数函数来，说只有对数函数可以满足。但是，我知道你认同，对数函数绝不符合题意！因为自变量为相反数时函数值总有一个是无意义的！

人家刘老师从来就是“语不惊人誓不休”，说只有我说的是谎言。

刘老师，怎么说你呢，见识少就多学习！我不想说你，是给你面子。不要以为你水平多高！会用几个课件就不得了。你设计过，还是真正维修过设备！恐怕变频器参数也设不好吧！别在这丢人现眼！

　　回复№384楼的<寒湘子>网友，有人认为是“吵架”或“掐架”，也有人认为是“各抒己见”！管它叫“掐架贴”还是叫“各抒己见帖”！我想那个躲在暗地里的删老王帖子的“论坛管理员”是不敢删<研讨会宣传员>的这个帖子的！因为<研讨会宣传员>也是“论坛管理员”，也有斑竹的权利！前者“管理员”是压制不住后者“管理员”言论自由的！！

　　老王申明一点：“网友”、“同学”、“老乡”这些词汇都是同一类的词，词性相同，但与“朋友”、“伙伴”、“盟友”的概念是不同的！老王与寒湘子素不相识，也不是什么“朋友”或“伙伴”或“盟友”的关系！各人对各人自己的言论负责！

　　老王引用<寒湘子>的发言内容是很正常的事情！刘志斌也引用<寒湘子>的发言内容，按刘志斌的逻辑，刘志斌是否也说寒湘子是刘志斌的朋友或伙伴？！

　　老王引用教科书上的内容来证明题目中“f(x)在0到正无穷大是增函数”这一句仅只表明该函数在其定义域内的[0，+∞)半开区间上的“单调性”是增函数而已，并不是说它的定义域是[0，+∞)；不等式“(f(x)-f(-x))/x＜0”中的符号“f(x)”与“f(-x)”的意涵是同一＂对应法则＂下，自变量在定义域内任意取一对儿互为相反的数值（x和-x）时，分别对应的“函数值f(x)”与“函数值f(-x)”；

　　题目核心部分的不等式“(f(x)-f(-x))/x＜0”蕴含着：函数f(x)的自变量在定义域内可取得互为相反的数值。即题设函数f(x)的定义域包含着“关于0点对称”的区间。

　　对于这部分内容，寒湘子发言：“不错，支持下”，所以老王认为<寒湘子>也理解了老王的观点，认同题目的函数f(x)的定义域不只仅是它的“单调增加”区间[0，+∞) ! 老王出于礼节，当然要感谢寒湘子的“理解和支持”啦！这是很正常的反应嘛！

　　只要有网友对老王的观点表示同意，或理解，刘志斌就要把对方很批、臭骂一顿！以示警戒：如有人还胆敢表露出对老王的观点有认同感，后果就如<烟雨朦朦>、<寒湘子>挨很批、挨臭骂的下埸一样！

　　譬如，关于 <在相同转差率下，同一(或相同)交流异步电动机的电流与电压之关系问题>，刘志斌跟老王发生的争论过程中，有好多网友是不敢插进来发言表示同意老王观点的！悄悄的用论坛信箱给老王发信息表示照着老王的《教你做一个实验》中设计的“判决实验”去真实的做了实验，实验的客观结果证明：果真是俩技术参数完全相同的异步电机，在相同转差率前提下，全额(角接)电压激励的线电流是降额(星接)电压激励的电流的3倍！即相同转差率前提下，电压高时电流大，电压低时电流小！与刘志斌乱弹理论的“相同转差率前提下，电压高时电流小，电压低时电流大”截然相反！

　　针锋相对的驳斥下面的（№386、№387、№388楼）刘志斌荒谬无知的质问！

  　　刘志斌质问道：『1、原题目已知函数“f(x)在0到正无穷大是增函数，f(1)=0，”，f(-x)怎么能是“自变量为相反数时函数值”呢？』

　1、记号“f(-x)”原本就是表示当自变量在定义域内分别取互为相反的数值（x和-x）时，其中“-x”所对应的函数值！怎么可能因刘志斌读不懂题目的 “f(x)在0到正无穷大是增函数，f(1)=0 ”的意涵，而就会造成记号“f(-x)”放弃原则来改变它原本的意义呢？！

　　刘志斌质问道：『2、原题目已知函数“f(x)在0到正无穷大是增函数，f(1)=0，”，哪来的“自变量为相反数时函数值”f(-x)呢？』

　2、原题目的陈述句“f(x)在0到正无穷大是增函数，f(1)=0”并不能唯一的确定函数f(x)具体的映射法则，也并没有给函数f(x)明确指定其定义域！所以题目所指的函数f(x)并不是刘志斌所谓的“已知函数”！

　　题目所指的函数f(x)是一个外延很大的概念！符合“f(x)在0到正无穷大是增函数，f(1)=0 ” 的函数f(x)还真是数不胜数的，甚至可以说是无穷无尽的！并不是象刘志斌打胡乱说的那样：“只有对数函数f(x)=loga(x)    a＞1”。

　　合格的高中学生都不难读懂原题目的陈述单句“f(x)在0到正无穷大是增函数”的真实意涵仅只是陈述：“在定义域内的右半开区间[0,+∞)上f(x)有单调递增的性质”而已，并不是表达题目在指定函数的定义域仅限于开区间(0,+∞)！

　　但是，数学基础知识很差的刘志斌却将题目的陈述单句“f(x)在0到正无穷大是增函数”错误的解读为“f(x)的定义域仅限于0点右侧的开区间(0,+∞)”啦！

　　关于函数的单调性，“增函数”或“减函数”是对定义域内某个区间而言的。通常很多的函数在定义域的某些区间上是增函数，而在另一些区间上不是增函数。

　　例如函数y=x^2-1 定义域是(-∞,+∞)，在这个定义域内的[0,+∞)半开区间上y=x^2-1是增函数，而在[1，1]闭区间上y=x^2-1不是单调的，当然就不是增函数，在(-∞,0)开区间上y=x^2-1虽然是单调的，但它仍然不是增函数，而是减函数。

　　大家注意到没有？把函数y=x^2-1简记作f(x)，那末，此f(x)就不折不扣的符合“f(x)在0到正无穷大是增函数，f(1)=0” ! 当自变量在定义域(-∞,+∞)内任意取一对儿互为相反的数值（a和-a）时，其数值“a”所对应的函数值就是“f(a)”，而数值“-a”所对应的函数值就是“f(-a)”!

　例如：

　若自变量分别取：1 和 -1 ， 那末，函数值f(1)=(1)^2-1=0　函数值f(-1)=(-1)^2-1=0

　若自变量分别取：-2 和 2，  那末，函数值f(-2)=(-2)^2-1=3　函数值f(2)=(2)^2-1=3

　　……　……

　　由于我们根本不可能将函数y=x^2-1定义域内无穷无尽的互为相反的数值全都列举出来！因此，我们只能采取代数的方法：用某一个字母来代表定义域内的任意一个数值，我们可以用a、也可以用b，当然也可以用x来代表定义域内任意的一个数值！随之，成对儿的“x和-x”即代表成对儿的“互为相反的数值”！把成对儿的互为相反的数值“x和-x”分别填入到同一个“函数对应法则记号f( )”的括弧中即分别对应得到“f(x)和f(-x)”这一对儿函数值记号！

　　函数f(x)=x^2-1在0到正无穷大是增函数，且f(1)=0，按照荒谬的“刘志斌逻辑”，刘志斌的意识里就会疑惑：『已知函数f(x)=x^2-1在0到正无穷大是增函数，f(1)=0，哪来的“自变量为相反数时函数值”f(-x)呢？”』

　　显而易见，刘志斌的“疑惑”、或者“质问”『2、原题目已知函数“f(x)在0到正无穷大是增函数，f(1)=0，”，哪来的“自变量为相反数时函数值”f(-x)呢？』都是荒谬无知的、滑稽可笑的！

　3、显而易见，刘志斌的：『3、既然原题目已知函数“f(x)在0到正无穷大是增函数，f(1)=0，”，f(-x)自然不是“自变量为相反数时函数值”！』纯粹是无知者的打胡乱说！

　　对于题设函数f(x)的定义域，陈述单句“f(x)在0到正无穷大是增函数”顶多也仅仅是给我们暗示了一条线索：“题设函数f(x)的定义域内包含着半开区间[0,+∞)”！

　　请网友们注意：f(x)的定义域内包含着半开区间[0,+∞)，并不等于说f(x)定义域就仅只限于半开区间[0,+∞)！更何况，题目核心“求(f(x)-f(-x))/x＜0时x的范围”还为我们暗示了另一条线索：题设函数f(x)的定义域必须包含“关于0点对称的区间”！否则，题目的核心“求(f(x)-f(-x))/x＜0时x的范围”就没有意义！

 　　我们综合这题目暗示的关于题设函数f(x)定义域的两条线索，我们就可以很轻松的枚举出一大堆既不折不扣的符合“f(x)在0到正无穷大是增函数，f(1)=0”，并且又满足当自变量在定义域内分别取互为相反的数值（x和-x）时有使“(f(x)-f(x))/x＜0的范围”的具体函数f(x)：

　　例1)、         f(x)=3x^4-8x^3+6x^2-1

　　例2)、         f(x)=2(x-0.5)^4+3(x-0.5)^3-0.5

　　例3)、         f(x)=3(x-1/2)^4+4(x-1/2)^3-11/16

　　例4)、         f(x)=x^2-1.1/(x+0.1)

　　例5)、         f(x)=2-4/(x+1)

　　例6)、         f(x)=0.25-1/(x+3)

　　例7)、         f(x)=x-ln[(1+x)/2]-1

 　　……   ……   等等

　　以上7例函数的定义域全都不折不扣地既包含了[0，+∞)半开区间（吻合第一条线索），又包含了“关于0点对称的区间”（吻合第二条线索）。

　　刘志斌质问道：『4、对数函数就是“在0到正无穷大是增函数，f(1)=0”，怎么说对数函数不否和题意呢？为什么要睁着眼说瞎话呢！』

　4、首先，刘志斌选择的对数函数f(x)=loga(x)  a＞1的定义域类型是“单边型”的！任何“单边型”定义域内都不包含“关于0点对称的区间”！所以，函数f(x)=loga(x) 根本不能吻合题目所暗示的关于题设f(x)定义域的第二条线索！

　　只要f(x)的定义域不包含“关于0点对称的区间”，就必然使题目的核心内容“求(f(x)-f(-x))/x＜0时x的范围”变得没有意义！所以，刘志斌选择的这个对数函数不符合题意！

　　其次，刘志斌选择的函数f(x)=loga(x) a＞1 还不能百分百的吻合题目所暗示的关于题设f(x)定义域的第一条线索：“f(x)的定义域内包含着半开区间[0,+∞)”！

　　显而易见，f(x)=loga(x)的定义域是开区间(0,+∞)，它根本包含不了半开区间[0,+∞) !只算是开区间(0,+∞)包含于半开区间[0,+∞) ，即(0,+∞)只是[0,+∞)的真子集。

　　刘志斌说f(x)=loga(x)就是符合“在0 到正无穷大是增函数”，那只能算是打了折扣的，擦边球式的“符合”，并不是百分百的符合！

　　题目核心“求(f(x)-f(-x))/x＜0时x的范围” 其算式“(f(x)-f(-x))/x”中的3个“x”必须是相同的数值x ！故“x”和“-x”必然是互为相反的数值！当“x”是正数时，其“-x”必然是负数；当“x”是负数时，其“-x”必然是正数！我们绝不允许胡搅乱弹的刘志斌把同一算式中出现的“x”和“-x”打胡乱说成“都是正数”！

　　若刘志斌赋予记号“f( )”代表『因变量y等于自变量x的对数』，则x应取正数 f(x)才有意义，但f(-x)却没有意义！

　　若刘志斌赋予记号“f( )”代表『因变量y等于x的相反数的对数』，则x应取负数 f(-x)才有意义，但f(x)却又没有意义！

　　显而易见，不论刘志斌赋予记号“f( )”代表『y=loga(x)』还是代表『y=loga(-x)』，也不论x∈(-∞,0)还是x∈(0,+∞)，刘志斌选择的对数函数都使得“f(x)-f(-x)”其减数和被减数中总有一个没有意义（或称总有一个不存在）！即总是使题目的不等式“(f(x)-f(-x))/x＜0”变得没有意义！所以刘志斌选择的对数函数不符合题意！

　　这么显而易见的道理、这么显而易见的事实，刘志斌却视而不见，愣是夹着屎犟说『只有他刘志斌选择的对数函数符合题意』，刘志斌这才是『睁着眼睛说瞎话呢！』

　　刘志斌居然颠倒是非、混淆黑白的发问：『5、有这么睁眼说瞎话，掩耳要盗铃的蠢人吗？』

　5、事实上，在这里夹着屎犟的刘志斌正是你自己所问寻的『睁眼说瞎话，掩耳要盗铃的蠢人』!

　6、把算式“(f(x)-f(-x))/x”中的成对儿记号“f(x)”和“f(-x)”解释为“自变量在定义域内取互为相反的数值（x和-x）所分别对应的成对儿函数值”完全是有依据的！我们的依据就是正统教科书上的理论，以及题目核心内容给我们暗示的关于题设f(x)定义域的第二条线索！

　　刘志斌蔑视正统理论、蔑视教科书，并妄图自创“刘志斌理论”来取代正统理论！总是以他荒谬的“刘志斌理论”拧巴着他的思维跟正统理论相对抗！

　　显而易见，刘志斌的『6、说f(-x)是“自变量为相反数时函数值”，显然不符合题意，因为题目“f(x)在0到正无穷大是增函数，f(1)=0，”』纯粹就是把题设f(x)在定义域内某一“单调的区间”误解为f(x)的整个“定义域”啦！可见对“单调的区间”和“定义域”这两个不同的概念，刘志斌都是无知的！

　7、只要结合题目的核心内容“求(f(x)-f(-x))/x＜0时x的范围”与刘志斌所选择的对数函数f(x)=loga(x) 就显而易见刘志斌的『7、那么f(-x)是什么？f(-x)是已知函数f(x)以y轴为对称的函数，是已知函数f(x)以y轴翻转后得到的函数f(-x)！』纯粹是无知者的打胡乱说！

　8、“同一算式中相同的记号f( )代表相同的对应法则”、“同一算式中成对儿的x和-x代表成对儿的互为相反的数值”、“把数值x和-x分别填入到同一法则记号f( )的括弧中就分别对应得到了函数值记号f(x)和f(-x)”，如果刘志斌不知道这些知识，那就请刘志斌不要解这个题了！

　9、刘志斌要解这个题，就请刘志斌尊重正统教科书、尊重正统数学理论，认认真真的把上述的知识弄懂、弄明白了再说解这个题！

引用 寒湘子 的回复内容： 

……对数函数绝不符合题意！因为自变量为相反数时函数值总有一个是无意义的！

1、原题目已知函数“f(x)在0到正无穷大是增函数，f（1）=0，”，f(-x)怎么能是“自变量为相反数时函数值”呢？

2、原题目已知函数“f(x)在0到正无穷大是增函数，f（1）=0，”，哪来的“自变量为相反数时函数值”

f(-x)呢？

3、既然原题目已知函数“f(x)在0到正无穷大是增函数，f（1）=0，”，f(-x)自然不是“自变量为相反数时函数值”！

4、对数函数就是“在0到正无穷大是增函数，f（1）=0”，怎么说对数函数不否和题意呢？为什么要睁着眼说瞎话呢！

5、有这么睁眼说瞎话，掩耳要盗铃的蠢人吗？

6、说f(-x)是“自变量为相反数时函数值”，显然不符合题意，因为题目“f(x)在0到正无穷大是增函数，f（1）=0，”；

7、那么f(-x)是什么？f(-x)是已知函数f(x)以y轴为对称的函数，是已知函数f(x)以y轴翻转后得到的函数f(-x)！

8、如果你不知道这个知识，请你不要解这个题了！

9、要解这个题，就去翻书把“函数f(x)以y轴翻转后得到的函数f(-x)，”的知识弄明白了！

10、寒湘子你先说，你承认有没有“函数f(x)以y轴翻转后得到的函数f(-x)，“这个知识？？？

11、寒湘子你敢说，高中数学没有“函数f(x)以y轴翻转后得到的函数f(-x)，”这个知识！！！

回复内容：

对： 刘志斌                             ... 内容的回复！（390）

 如果一个人没有搞懂函数的含义，他无论引用什么样的教材，它仍然不能证明他对函数足够了解。

我们讲 有y=f(x)的确切含义是y 是自变量x的函数，x的全体构成定义域，y的全体构成值域，f是对应法则。当y是x的函数时，必需满足任一x只有唯一的y对应。这决定f只可能是一对一和多对一的关系。

刘老师在谈函数时总是避谈自变量x，比如他说y=sin2x是正弦函数，实际y并不是x的正弦函数，为什么呢？因为y=2sinx*cosx和x的正弦函数y=sinx是非线性关系。但是我说y=sin2x y不是x的正弦函数，刘老师就很觉得可笑。因为他没有搞懂函数的定义！当然关于异步电动机转速和速度关系的发现也是没有搞懂函数的定义。

　　针锋相对的驳斥前面№376楼刘志斌恶意的歪曲和刘志斌荒谬的逻辑！

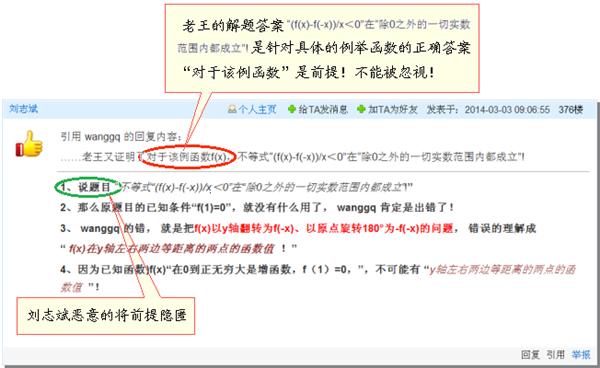
　　老王具体的对某一例完全符合题意的函数（例如：f(x)=3x^4-8x^3+6x^2-1  其(f(x)-f(-x))/x=-16x^2     x≠0 ）来证明“该函数f(x)”使题目的不等式“(f(x)-f(-x))/x＜0”在除0之外的一切实数范围内都成立。完全是正确的！

　　可是刘志斌却居心叵测的将老王对具体函数例子进行的证明故意歪曲成『1、说题目“不等式‘(f(x)-f(-x))/x＜0’在‘除0之外的一切实数范围内都成立’!”』

　　刘志斌故意隐匿掉老王“具体针对某一例函数f(x)进行证明”的这一前提！是有他险恶用心的！因为解题者选择不同“具体对应法则”的函数f(x)作解题对象，就有可能使题解的答案不同！譬如：若选择f(x)=2-4/(x+1) 作解题对象，那末，对于f(x)=2-4/(x+1)这一例函数来说，题目的正确答案就应该为“(f(x)-f(-x))/x＜0时x的范围是除闭区间[-1，+1]之外的一切实数”！

　　刘志斌用连词“那么”把『1、说题目“不等式‘(f(x)-f(-x))/x＜0’在‘除0之外的一切实数范围内都成立’!”』与『2、（那么）原题目的已知条件“f(1)=0”，就没有什么用了， wanggq 肯定是出错了！』串接起来，难道刘志斌想表达：条件“f(1)=0”限制了“(f(x)-f(-x))/x＜0”的范围吗？！可见对于函数的相关概念刘志斌确实太无知！

　　事实上，题目并没有限制“(f(x)-f(-x))/x＜0 ”的范围！条件“f(1)=0” 仅只是要求同学们在选择作为解题对象的函数f(x)时，必须选择其曲线通过(1，0)点的函数而已！

　　难道刘志斌认为只要f(x)的曲线过(1，0)点，那么，不等式“(f(x)-f(-x))/x＜0”就必然不可能在“除0之外的一切实数范围内都成立”吗 ？！ 

　　刘志斌他这里的条文1、跟条文2、根本就不存在“必然的联系”！可见刘志斌把他的条文1、和条文2、串接起来表达的内容，纯粹是无知者的打胡乱说！

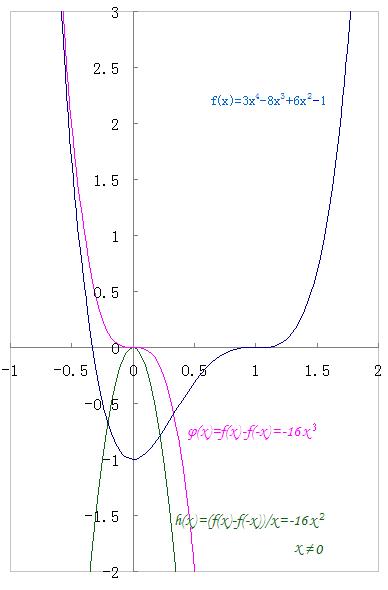
　　请看，老王例举的f(x)=3x^4-8x^3+6x^2-1 不折不扣的符合题设“f(x)在0到正无穷大是增函数，f(1)=0” ，并且满足f(x)的定义域内有使不等式“(f(x)-f(-x))/x＜0”的范围！

　　大家从函数图象上可以清楚的看到f(x)在0 到正无穷大是增函数，f(1)=0 ！而且老王在之前已经严密谨慎的证明过！请参阅老王在前面详细的证明过程！

　　老王在选择这个函数f(x)=3x^4-8x^3+6x^2-1作为解题对象时，有过慎密的分析：多项式3x^4-8x^3+6x^2-1含有(x-1)的因式，请看因式分解：

　　　　　　　3x^4-8x^3+6x^2-1=(3x+1)(x-1)(x-1)(x-1)

　　很明显：当x=1 时，3x^4-8x^3+6x^2-1=0 即f(1)=0 ! 难道你刘志斌还认为这不是在运用题设的“f(1)=0”的条件来选择符合题意的函数f(x)吗？！

　　把函数f(x)=3x^4-8x^3+6x^2-1 定义域(-∞,+∞)内任意一对儿互为相反的数值（x和-x）分别填入同一个“对应法则f( )=3( )^4-8( )^3+6( )^2-1” 即得互为相反的数值（x和-x）分别对应的成对儿函数值f(x)和函数值f(-x)：

　　　　　　　f(x)=3x^4-8x^3+6x^2-1

　　　　　　　f(-x)=3x^4+8x^3+6x^2-1

　　所以，f(x)-f(-x)=-16x^3   ； (f(x)-f(-x))/x=-16x^2   　 (x≠0)　如下图所示。

　　难道刘志斌还认为“对于此例函数”而言，不等式“(f(x)-f(-x))/x＜0”不是在除0之外的一切实数范围内都成立吗？！ 

　　老王也曾例举过一个分段表示的函数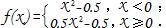（请注意，分段函数在定义域的不同区间内，对应法则不同，但是，它仍然也只是一个函数，而不是两个函数）！

　　这一例函数同样是不折不扣符合原题设的“f(x)在0到正无穷大是增函数，f(1)=0 ” 的条件，同时，它又满足“f(x)曲线上有(f(x)-f(-x))/x＜0的范围”的条件！（即原题目核心“求(f(x)-f(-x))/x＜0时x的范围”所蕴含的“条件”）！如下图所示：

 　　从该函数f(x)的图象上我们可以很直观的看到它不折不扣的符合“f(x)在0到正无穷大是增函数，f(1)=0”；

　　从函数f(x)对应于[0，+∞)半开区间上的“对应法则f( )=0.5( )^2-0.5”上也明显的可以看出有0.5(1)^2-0.5=0 即符合原题设的：f(1)=0 的条件！

　　你刘志斌再不济，你也可以将0.5x^2-0.5分解为：0.5(x+1)(x-1) ，这不明显的告诉你刘志斌：f(x)=0.5x^2-0.5 当x=1时 f(x)=0  即符合原题设的：f(1)=0 之条件吗？！

　难道你刘志斌认为这还不是在运用题设的“f(1)=0”的条件来选择符合题意的函数

f(x)吗？！

　　我们来证明该分段函数能让题目之核心部分中的那个不等式“(f(x)-f(-x))/x＜0”在除0之外的一切实数范围内都成立！ 

　　证明：设“x”、“-x”是函数f(x)定义域{ x│x∈R }内任意的一对互为相反数的自变量值. 

　　1)、当x＞0时，  则：-x＜0 ,　

　　那么，f(x)=0.5(x)^2-0.5 ；f(-x)= (-x)^2-0.5 

则：f(x)-f(-x)=[0.5(x)^2-0.5]-[(-x)^2-0.5]

　　　　　  =[0.5(x)^2-0.5]-[(x)^2-0.5]

　　　　　  =(0.5-1)(x)^2

　    　　　  = -0.5(x)^2＜0 

　　f(x)-f(-x)＜0，而x＞0，

即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立；

　　2)、当x＜0时，  则：-x＞0 ,　

　　那么，f(x)=(x)^2-0.5 ；f(-x)=0.5(-x)^2-0.5 

则：f(x)-f(-x)=[(x)^2-0.5]-[0.5(-x)^2-0.5]

　　　　　  =[(x)^2-0.5]-[0.5(x)^2-0.5]

　　　　　  =(1-0.5)(x)^2

   　 　         =0.5(x)^2＞0 

　　f(x)-f(-x)＞0，而x＜0， 

即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立。

　　所以，对于该分段函数f(x)有：自变量取除0之外的一切实数都能使不等式

“(f(x)-f(x))/x＜0”成立！

　　如下图所示：

　　图中f(x)-f(-x)的曲线记作φ(x)，通过运算我们可解得：

　　　　　　　　  　定义域 x∈R ；

　　图中(f(x)-f(-x))/x的曲线记作h(x)，通过运算我们可解得：

　　　　　　　　 　 定义域 x∈R ，且x≠0

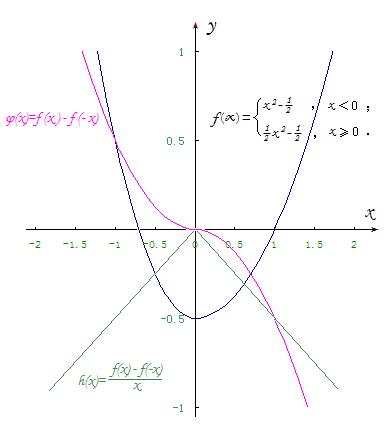
 　　难道刘志斌还认为“对于此例函数”而言，不等式“(f(x)-f(-x))/x＜0”不是在除0之外的一切实数范围内都成立吗？！

　　刘志斌的知识浅薄，自己看不懂题目的陈述单句“f(x)在0到正无穷大是增函数”是说f(x)在其定义域内的一个半开区间[0，+∞)上有单调递增的性质，并不是说f(x)的定义域仅限于开区间(0，+∞)！刘志斌却居然愣充“大师”，以自己错误的“解读”为所谓的“理论标准”来批评老王以教科书上正统理论为依据的正确理解“有错”：看这刘志斌的『3、 wanggq 的错， 就是把f(x)以y轴翻转为f(-x)、以原点旋转180°为-f(-x)的问题， 错误的理解成“ f(x)在y轴左右两边等距离的两点的函数值  ！』

　　这刘志斌的“条文3”所依据的“理由”就是刘志斌这荒谬的“条文4”：『4、因为已知函数)f(x)“在0到正无穷大是增函数，f(x)=0，”，不可能有 “y轴左右两边等距离的两点的函数值  ”』

　　刘志斌这“条文3”和“条文4”结合起来充分表露出刘志斌对函数的认知是荒谬的、浅薄的！

　　我们应当清楚：函数f(x)使其(f(x)-f(-x))/x＜0时x的范围并不是由f(1)=0 来决定的！即便再结合了“f(x)在0到正无穷大是增函数”的条件也不绝可能唯一确定出题目泛指的函数f(x)曲线上(f(x)-f(-x))/x＜0时x的范围！必须在选定了确定的有“(f(x)-f(-x))/x＜0”范围的某一具体函数f(x)之后，才能唯一确定其曲线上(f(x)-f(-x))/x＜0时x的范围！

　　事实上，算式f(x)-f(x)是指函数的自变量在定义域内分别取互为相反的数值（x和-x）所分别对应的成对儿函数值之差，而(f(x)-f(-x))/x则是函数值f(x)减函数值f(-x)所得之差与自变量数值x的比值。(x≠0)

　　如果f(x)减f(-x)所得之差值等于0，则比值(f(x)-f(-x))/x=0 。

　　如果f(x)减f(-x)所得之差值与自变量数值x同号，则比值(f(x)-f(-x))/x＞0；

　　如果f(x)减f(-x)所得之差值与自变量数值x异号，则比值(f(x)-f(-x))/x＜0；

　　可见，函数f(x)曲线上(f(x)-f(-x))/x＜0时x的范围其实是由f(x)-f(x)之差值与自变量数值x异号的范围来决定的！而与f(x)曲线是否经过(1，0)点的这一要求没有必然的联系！

　　举个具体的函数例子来说吧：

　　例如设f(x)=√(x^2)-0.2x    定义域(-∞，+∞)  其曲线如图1所示：

　　　　　　　　　　　　　　　　　　图1

　　这条曲线f(x)不折不扣的符合：“f(x)在0到正无穷大是增函数”这一条件！而且也满足：f(x)曲线上有“(f(x)-f(-x))/x＜0”的范围！但是，这一f(x)曲线并不经过(1，0)点！即它不符合“f(1)=0”这一条件！

　　为了符合题目所设的“f(1)=0”这一条件，我们只要将图1所示的曲线向下平移0.8个单位，变成f(x)=√(x^2)-0.2x -0.8 就行啦！从而函数f(x)=√(x^2)-0.2x-0.8也就是全部符合题目条件（包括符合题目核心所蕴含的“条件”）的函数啦！其曲线如图2所示：

　　　　　　　　　　　　　　　　　　　图2

 　　我们用x和-x分别代表函数f(x)=√(x^2)-0.2x-0.8定义域内的任意一对儿互为相反的数值，分别代入函数f(x)=√(x^2)-0.2x-0.8的同一对应法则f( )中运算，我们就分别解得对应的成对儿函数值f(x)和f(-x)：

　　函数值f(x)=√(x^2)-0.2x-0.8 ；函数值f(-x)=√(x^2)+0.2x-0.8

　　所以，f(x)-f(-x)=√(x^2)-0.2x-√(x^2)-0.2x

　　　　　　　　 = -0.4x      　　　x∈R

　　所以，(f(x)-f(-x))/x= -0.4x/x      　x∈R ，且x≠ 0

　　　　　　　　　　= -0.4       

　　即：对于此例函数f(x)而言：(f(x)-f(-x))/x＜0的范围是除0之外的一切实数！

　　若将“f(x)-f(-x)”记作φ(x)；将“(f(x)-f(-x))/x” 记作h(x). 则它们的曲线如图3所示：

　　　　　　　　　 　　　　　　　　　图3

　　大家注意到没有？将某一f(x)的曲线向下或向上平移，仅只是改变了f(x)的常数项，而没有改变f(x)中含x的项！

　　所以，对于某一既定f(x)的曲线，不论将它向下或向上平移，也不论将它向下或向上平移多少个单位，它原本曲线上与y轴左右两侧等距离的点（即x和-x分别对应的点）的纵坐标相对谁大谁小的关系是保持不变的！

　　譬如对于f(x)=√(x^2)-0.2x来说，又譬如对于f(x)=√(x^2)-0.2x-1.8来说，它们同样都使(f(x)-f(-x))/x＜0的范围为“除0之外的一切实数”！可见“f(1)=0”这一条件并不足以限制曲线上(f(x)-f(-x))/x＜0的范围！如图4、图5所示：

　　　　　　　　　　　　　　　　　　图4

　　　　　　　　　　　　　　　　　　图5

　　请注意，对于某一既定形状的f(x)曲线，我们可以通过将其向左或向右的平移来改变曲线上“(f(x)-f(-x))/x＜0”的x的范围。

　　例如：f(x)=3x^4+4x^3 从它的图象上看，它是不折不扣符合题目“f(x)在0到正无穷大是增函数”这一条件的！但是，它既不满足“f(1)=0”的条件，也不满足“有(f(x)-f(-x))/x＜0的范围”的条件 ! 

　　我们将此曲线向右平移1个单位，使它变为f(x)=3(x-1)^4+4(x-1)^3 ，这样，f(x)就完全符合题目的全部条件（包括符合题目核心所蕴含的条件）啦！如图6所示：

　　　　　　　　　　　　　　　　　　图6

　　图中为了在同一坐标系里区分不同的函数对应法则，把曲线y=3x^4+4x^3记作：G(x)以区别于f(x)=3(x-1)^4+4(x-1)^3。

　　图中的f(x)=3x^4-8x^3+6x^2-1 即G(x)向右平移1个单位而成的f(x)=3(x-1)^4+4(x-1)^3

　　把3(x-1)^4+4(x-1)^3展开，即解得：

　　f(x)=3x^4-8x^3+6x^2-1

　　f(x)-f(-x)= -16x^3  　　x∈R      

　　(f(x)-f(-x))/x= -16x^2     x∈R，且 x≠0

　　即对于此例函数f(x)=3x^4-8x^3+6x^2-1而言，不等式(f(x)-f(-x))/x＜0 “在除0之外的一切实数范围内都成立”！

　　现在我们将y=3x^4+4x^3的曲线向右只平移半个单位来得到另一个函数f(x)=3(x-1/2)^4+4(x-1/2)^3  也同样不折不扣符合题目的“f(x)在0到正无穷大是增函数”，而且满足题目核心所蕴含的“f(x)曲线上有f(x)-f(-x))/x＜0的范围”这一条件！如图7所示：

　　　　　　　　　　　　　　　　　　　图7

　　唯一不足的是：f(x)=3(x-1/2)^4+4(x-1/2)^3 不能满足“f(1)=0”。但是，我们可以将其再向下平移“11/16”个单位来满足“f(1)=0”！

　　将y=3x^4+4x^3的曲线向右平移“1/2”、再向下平移“11/16”所得到的新函数是：f(x)=3(x-1/2)^4+4(x-1/2)^3-11/16 这就是一个完全符合题目的全部条件（包括符合题目核心所蕴含的“条件”）的f(x)！如图8中的红色曲线所示：

　　　　　　　　　　　　　　　　　　　图8

 　　这个f(x)=3(x-1/2)^4+4(x-1/2)^3-11/16曲线在其定义域的某些范围内“f(x)-f(-x)”的值与x异号，异号即表明“(f(x)-f(-x))/x＜0”；而在另一些范围内“f(x)-f(-x)”的值与x同号，同号即表明“(f(x)-f(-x))/x＞0”。

　　通过运算，我们解得：

　　f(x)-f(-x)= -4x^3+3x 　 记作φ(x)　  x∈R　

　　把 -4x^3+3 分解为 x(2x+√3)(√3-2x)  很明显，φ(x)的3个根分别是：x1= -√3/2， x2=0 ，x3=√3/2  即φ(x)过零的3个点的横坐标。如图9中的棕色曲线所示：

　　　　　　　　　　　　　　　　　　图9

　　φ(x)的3个根，将f(x)的定义域(-∞，+∞)分割为4个开区间：开区间(-∞，-√3/2)内φ(x)与x异号；开区间(-√3/2，0)内φ(x)与x同号；开区间(0，√3/2)内φ(x)与x同号；开区间(√3/2，+∞)内φ(x)与x异号。

　　即：f(x)在(-∞，-√3/2)内(f(x)-f(-x))/x＜0 ；f(x)在(-√3/2，0)内(f(x)-f(-x))/x＞0；f(x)在(0，√3/2)内(f(x)-f(-x))/x＞0；f(x)在(√3/2，+∞)内(f(x)-f(-x))/x＜0。

　　所以，对于函数f(x)=3(x-1/2)^4+4(x-1/2)^3-11/16而言，(f(x)-f(-x))/x＜0时x的范围是“除闭区间[-√3/2，√3/2] 之外的一切实数”！

　　对于函数f(x)=3(x-1/2)^4+4(x-1/2)^3而言，(f(x)-f(-x))/x＜0时x的范围同样也是“除闭区间[-√3/2，√3/2] 之外的一切实数”，可见“f(1)=0”的条件并不足以限制函数f(x)曲线上“(f(x)-f(-x))/x＜0时x的范围”！

　　只是，若选择f(x)=3(x-1/2)^4+4(x-1/2)^3 则不能完全符合题意，而应当选择将它再向下平移“11/16”个单位，变为f(x)=3(x-1/2)^4+4(x-1/2)^3-11/16才算得上是不折不扣的完全符合题意的f(x)！

　　我们看到，无知的刘志斌将题目的“f(x)在0到正无穷大是增函数，f(1)=0”错误的解读为『1、题设f(x)的定义域是题目给定的开区间(0，+∞)  2、f(x)在整个定义域上是增函数 3、f(1)=0 』并认定符合“f(x)在0到正无穷大是增函数，f(1)=0”的函数f(x)『只有对数函数y=logaX  a＞1』! 从而荒谬的胡搅出“刘氏代数和公式”：『当x＜0 （并非f(x)=0）时，(f(x)-f(-x))/x=-f(-x)/x ；当 0＜x （并非f(-x)=0）时，(f(x)-f(-x))/x=f(x)/x』，并以荒谬的“刘氏代数和公式”为基准再推出荒谬的错误结论：“由函数值与自变量值异号的范围来决定(f(x)-f(-x))/x＜0 的范围”！ 

　　所以，刘志斌荒谬的认定该题目的解(f(x)-f(-x))/x＜0时x的范围是被-f(-1)=0及f(1)=0 限制在(-1，0)和(0，1) 这两个区间内的！

　　如果我们将y=f(x)-f(-x)看作一个新的函数，那末，把刘志斌的f(x)=loga(x) ；-f(-x)=-loga(-x) 代入即得：y=loga(x)-loga(-x)，非常明显：这一“函数”在整个实数范围内都是无法成立的！

　　因为使y=loga(x)有意义的x范围是(0，+∞)；使y=-loga(-x)有意义的x范围是(-∞，0)，那末，使y=loga(x)-loga(-x)有意义的x范围就应当是{(-∞，0)∩(0，+∞)}。很显然，这个交集是空的！也就是说这个所谓的“函数y=loga(x)-loga(-x)”实际上是不存在的！因为：在一切实数范围内都不存在它的定义域！不论x在实数范围内取任意哪一个数，算式loga(x)-loga(-x)都不会有意义！

　　没有意义的算式，是非法的，是无据对其施展任何“运算”的，是万不可能有什么运算答案的！刘志斌却居然打胡乱说『当x＜0 （并非f(x)=0）时，(f(x)-f(-x))/x=-f(-x)/x ； 当0＜x （并非f(-x)=0）时，(f(x)-f(-x))/x=f(x)/x』！可见对于函数知识来说，刘志斌是相当的无知！

　　刘志斌无知的胡搅乱弹完全颠覆了正统教科书上的正确理论！完全篡改了原题目中的不等式“(f(x)-f(-x))/x＜0”的意涵实质！

引用 寒湘子 的回复内容： 

…… 如果一个人没有搞懂函数的含义，他无论引用什么样的教材，它仍然不能证明他对函数足够了解。……

寒湘子你就说，高中数学有没有“函数f(x)以y轴翻转后得到的函数f(-x)，”这个知识？？？

刘老师引用的教材，我只能讲：对于学习数学是一个很糟糕的处理方式！也许刘老师正式受其影响，以致于，到今天也还不能理解函数的概念。

首先，我们需要明确一点，在平面直角坐标系上，有两个正交的实数对(x,y)对应坐标平面上唯一的一个点P(x,y)；

第二：如果我们定义y=f(x)，那么点P的轨迹就成了y=f(x)的图像；一个

第三：显然我们可以绘出y=f(x)的图像；

第四：y=f(-x)是什么？是将它看做另一个函数还是把它作为y=f(x)对于x=0轴（y轴）的镜像？

如果要表示为另外一个函数y=f(-x)=g(x)，那么g肯定不是f。既然g不是f，么就不能直接由f()来直接得到y。实际上它要先对x求相反数之后用f作用之才得到y！

但是我们可以不将y=f(-x)看成一个新的函数。而看成y=f(x)关于y轴的镜像。就像我们照镜子，并不是又生成一个自己。实际上两者定义域、值域和对应法则都相同。没有本质不同！不同之处就在于x的参考方向。

如果脱离图形表示 y=f(-x)就是将x用-x替换的函数值！

所以无论刘老师画不画y=f(-x)的图像y=f(x)对于x<0没有定义这个题目就不可解！就这么简单。数学里关于为定义的特性就不能运算！计算机里为定义变量，在程序里就要出错。是一个道理！

将y=f(-x)和y=f(x)看成一个函数还是两个函数。正如同婴孩会将镜子里的自己看做另一个人，而大人不会！

　　“x的对数”函数的图象是决不可能出现在2、3象限的！刘志斌把“x的对数”函数的图象画到2、3象限，是一个很低级的错误！

　　刘志斌引用的不是正统教材上的内容！而是在网上搜索来的！网上说什么的都有，正确，错误的都有。所以网上的东西不足为凭！

　　寒湘子糊涂，说什么“他无论引用什么教材”？哪种正统教材上有把“x的对数”函数曲线弄在2、3象限的？！

　　刘志斌引用依据是这个从网上复制过来的：

　　这只能说明网上象刘志斌这样“二”的“假冒大师”还不止刘志斌一个！

 　　众所周知：负数和0没有对数。所以，“x的对数”函数曲线全部在OY轴的右边。有教科书的理论为证：

　　对于如 “x的对数函数” 这类单边型定义域的f(x)，根本就没有“f(-x)”可言，根本就没有谈“求(f(x)-f(-x))/x＜0时x的范围”的基础！所以，原题目中的函数f(x)就绝不是“x的对数函数”!  而必须是定义域包含“关于0点对称区间”的这类函数！

没有定义的特性和变量不能运算！计算机里没有定义的变量和函数，在程序里就会出错。一个道理。推理必须有依据！