昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
综合种种问题的不同看法，我们不难得到这样的结论：
1、刘老师在和我们谈“函数”“定义域”“值域”“幂函数”“三角函数”“对数函数”等等，和传统数学定义都不是一回事， 除了字一样，内涵可能完全不同！
2、刘老师的推理往往先肯定后件（结论部分）之后再告诉你这是唯一对的，其方法是预言师的方法，而不是普通人的方法和数学的方法，因而成就其大师！
3、在局部上看其思维也相当缜密，只是根基（前件：前提条件）总是最薄弱的，你跟着他的思路走，越往后来越荒谬！只要你找到他的一个明显的错误，就不攻自破。因为推理太缜密了，怎么可能会出错？除非本身就是胡诌！
所以在许多问题的辩论，我都感觉是和外星人说话！你不理他他就以为他对，而且开口说你谎言，闭口说你谎言。真的不胜其烦！
4、举例说，y=loga(-x) 定义域是x＜0，
1）寒湘子的观点是，不是对数函数，因为它不是对数定义式；
2）我的观点是，是对数函数，但是，不是定义式的对数函数；
3）我的观点是，凡是由基本初等对数函数“演算”或者“变换”后的函数，是“非定义式的”、“非简单的”、“非基本的”的对数函数，都还是对数函数；
4）我的理由是，凡是由基本初等对数函数“演算”或者“变换”后的函数，都具有最基本的定义的对数函数的映射关系loga( ) ，是这类函数的“特征算符”；
5）我的理由是，凡是由基本初等对数函数“演算”或者“变换”后的函数，都具有最基本的定义的对数函数的映射关系loga( ) ，函数的图像、性质可以由最基本的定义的对数函数求得，它们之间的关系是同类函数中“个别”和“一般”的关系；
6）由基本初等对数函数“演算”或者“变换”后的函数，自变量、因变量之间还可能有包含对数算符loga( ) 之外的其它辅助运算，这些都不能改变算符loga( ) 决定的主运算。
6、举例说，由定义式对数函数y=loga(x)，
1）以y轴对称变换得y=loga(-x)；
2）以原点对称变换得y=-loga(-x)；
3）y轴拉伸3倍得y=-3loga(-x)；
4）x轴压缩4倍得y=-3loga(-4x)；
5）沿y轴向上平移5个单位得y=-3loga(-4x)+5；
6）沿x轴向右平移6个单位得y=-3loga(-4x-6)+5
7、寒湘子的观点是y=-3loga(-4x-6)+5，不是对数函数；
8、我的观点，y=-3loga(-4x-6)+5是对数函数，定义式的函数映射关系loga( )，才是对数函数的特征算符；
10、对数函数y=-3loga(-4x-6)+5，遵从对数运算法则吗？当然遵从对数运算法则：
1）举例说，已知：对数函数y=-3loga(-4x-6)+5、u=-3loga(-4v-6)+5，
求： loga(-4x-6)+loga(-4v-6)=？
解：y=-3loga(-4x-6)+5 变形的 (y-5)/(-3)=loga(-4x-6)
u=-3loga(-4v-6)+5 变形的 (u-5)/(-3)=loga(-4v-6)
loga(-4x-6)+loga(-4v-6)=loga(-4x-6)(-4v-6)=(y-5)/(-3)+(u-5)/(-3)
2）对数函数y=-3loga(-4x-6)+5的运算，适用对数运算、函数变换、代数运算的一般法则；
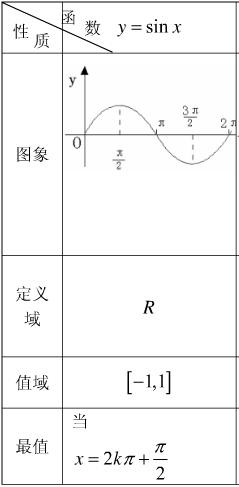
3、“至于其余演算，那是变换的问题。……”，那么“演算”或者“变换”前是定义的正弦函数，“演算”或者“变换”后就不是定义式那样“简单的形式”，还叫“正弦函数”吗？还是不能叫“正弦函数”？
4、举例说，y=2sin(x)
1）寒湘子的观点是，y=2sin(x)不是正弦函数，因为它不是正弦函数定义式；
2）我的观点是，y=2sin(x)是正弦函数，但是，不是定义式的正弦函数；举例说，y=2sin(x)的值域是[-2,+2]；
3）我的观点是，凡是由基本初等正弦函数“演算”或者“变换”后的函数，是“非定义式的”、“非简单的”、“非基本的”的正弦函数，但都还是正弦函数；
4）我的理由是，凡是由基本初等对数函数“演算”或者“变换”后的函数，都具有最基本的定义的正弦函数的映射关系sin( ) ，映射关系sin( ) 是这类函数的“特征算符”；
5）我的理由是，凡是由基本初等对数函数“演算”或者“变换”后的函数，都具有最基本的定义的正弦函数的映射关系sin( ) ，函数的图像、性质可以由最基本的定义的正弦函数求得，它们之间的关系是同类函数中“个别”和“一般”的关系；
6）由基本初等对数函数“演算”或者“变换”后的函数，自变量、因变量之间还可能有包含正弦算符sin( ) 之外的其它代数运算，这些都不能改变算符sin( ) 决定的基本运算法则。
5、举例说，由定义式正弦函数y=sin(x)，
1）x轴压缩ω倍得y=sin(ωx)；
2）沿x轴向左平移φ个单位得y=sin(ωx+φ)；
3）y轴拉伸A倍得y=Asin(ωx+φ)；
4）沿y轴向上平移B个单位得y=Asin(ωx+φ)+B；
6、寒湘子的观点是y=Asin(ωx+φ)+B，不是正弦函数；
7、我的观点，y=Asin(ωx+φ)+B是正弦函数，定义式的正弦函数映射关系sin( )，才是正弦函数的特征算符；
8、我的观点，y=Asin(ωx+φ)+B是正弦函数，自变量、因变量之间包含正弦算符sin( ) 之外的其它代数运算，这些都不能改变算符sin( ) 决定的基本运算法则。
10、正弦函数y=Asin(ωx+φ)+B，遵从正弦运算法则吗？当然遵从正弦运算法则：
1）举例说，
已知：正弦函数y=Asin(ωx+φ)+B、余弦函数u=Acos(ωx+φ)+B5，
求：[ sin(ωx+φ)]^2+[cos(ωx+φ)]^2
解：由y=Asin(ωx+φ)+B ，变形得 sin(ωx+φ)=(y-B)/A
由u=Acos(ωx+φ)+B ，变形得cos(ωx+φ)=(u-B)/A
[ sin(ωx+φ)]^2+[cos(ωx+φ)]^2 =[(y-B)/A]^2+[(u-B)/A]^2
=[(y-B)^2+(u-B)^2]/A^2
=1
2）正弦函数y=Asin(ωx+φ)+B的运算，适用正弦运算、函数变换、代数运算的一般法则；
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
