昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
引用 寒湘子 的回复内容：
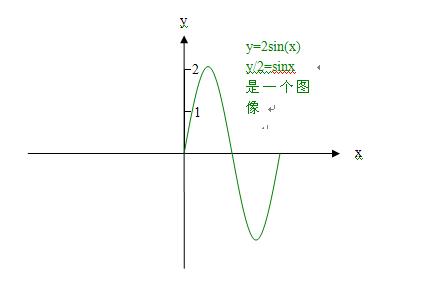
y'=y/2，y'是y的一次函数，y'与y是一一对应的正比关系，既然y'(=y/2)是x的正弦函数，y不也是角的正弦函数吗？
刘老师：告诉我如何证明好吗？我真的很笨，如果不能证明，怎么能、敢相信你说的是对的！
寒湘子这个都不知道 ？要从函数的定义出发：
1、已知y'(=y/2)是角x的正弦函数：
1）{角x}为一个集合；
2）{值域y'}为一个集合；
3）两个集合之间的一一对应的映射关系是sin( )；
2、y'=y/2，是一个正比函数，
1）{y}的集合；
2）{y'｜y/2}的集合；
3）{y}的集合与{y'｜y/2}的集合，元素一一对应；
3、因为{y'｜y/2}的集合与{角x}的集合之间存在一一对应的映射关系sin( )，所以{y}的集合与{角x}的集合之间存在一一对应的映射关系sin( )；
4、所以，因为y'(=y/2)是角x的正弦函数，所以y也是角x的正弦函数；
8、看看寒湘子750楼、751楼、752楼的证明，寒湘子的证明是不是有点儿傻？把证明2sin(x)≠sin(x)，说成是2sin(x)不是正弦函数！？把证明loga(x)≠loga(-x),说成是loga(-x)不是对数函数！？把证明2x^a≠x^b，两个函数曲线不可能重合，说成是y=2x^a不是幂函数！？
9、根据函数的定义，已知函数y=f(x)，就是说有集合{x}和集合{y}之间存在一一对应的映射关系f( )；
10、如果已知函数y=f(x)，通过图像变换得y=af(bx+c)+d，那么变换后的y同样是变换后的x的同类函数，保持原函数的映射关系f( )不变；
11、原因是y=af(bx+c)+d，可以变形为(y-d/a)=f(bx+c)，令y'=y-d/a，x'=bx+c，则有y'=f(x')！
12、y'=y-d/a，说明y'与y一一对应，x'=bx+c，说明x'与x一一对应，这样y也是x的同类函数f( ) ；
刘志斌把概念东搅西搅就胡搅出：直角坐标平面上y轴左侧有“对数函数”的图象！
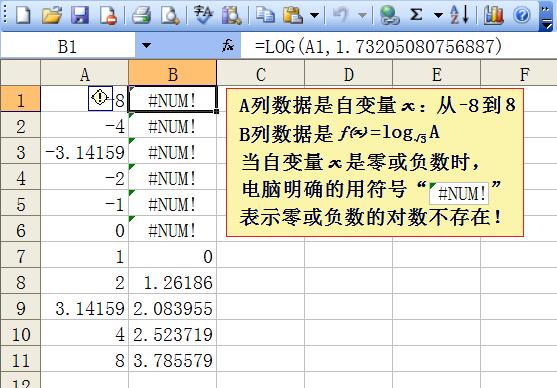
刘志斌愣要说负数有对数，而且反复的把他那幅错误对数函数曲线图贴出来胡说“看着图，对数函数在2、3象限有定义，有图象”还列了一个数据表格来忽悠他的刘粉丝。
对付象刘志斌这样胡搅乱弹的“大师”的方法就是，不管他吹的天花乱坠，只要把它胡吹的神秘“刘理论”给落到实处，就能让刘志斌现出“二百五”的本来面目！
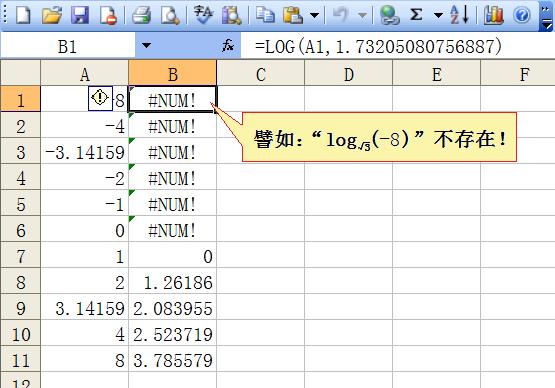
我们叫刘志斌试将以√3为底，“-3.14159”的所谓“对数”计算一下，看看这个负数的所谓“对数”是多少，看看他刘志斌的计算结果能否服众？！！
刘志斌一直不敢计算这个真数为“负数”的所谓“对数”！只能胡乱的混搅出“对数是(y-5)/3、真数是-4x-6的对数函数”！多么荒唐的“刘氏对数”！多么荒谬的“刘志斌理论”！
好，我们来看刘老师的所谓证明逻辑：
1、已知y'(=y/2)是角x的正弦函数： /根据定义/
1）{角x}为一个集合； /是，集合元素是角x/
2）{值域y'}为一个集合； /是，集合元素是y',而不是值域y'，不过对刘老师不能要求那么严格/
3）两个集合之间的一一对应的映射关系是sin( )； /定义域到值域的映射关系是正弦关系，但是是多对一的关系，如30度角和150度角，在值域上都对应0.5，不过算了，刘老师很难搞清楚对应关系，知道有关系就不错了/
2、y'=y/2，是一个正比函数，
1）{y}的集合；
2）{y'｜y/2}的集合；
3）{y}的集合与{y'｜y/2}的集合，元素一一对应； /注意这里的对应关系是1:1/2而不是sin()/
3、因为{y'｜y/2}的集合与{角x}的集合之间存在一一对应的映射关系sin( )，所以{y}的集合与{角x}的集合之间存在一一对应的映射关系sin( )； /前面已经讲过第一句已经不对了，后一句不仅不对，而且没有根据，请说出依据！/
4、所以，因为y'(=y/2)是角x的正弦函数，所以y也是角x的正弦函数； /由于3不成立所以4也不能成立/
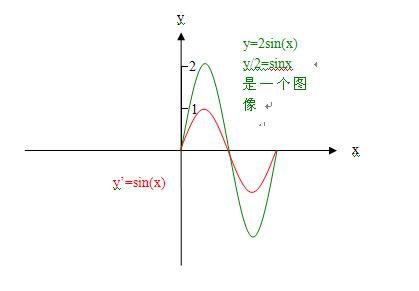
红色是刘老师的证明，绿字是我的注释，大家一看就明，根本不符合数学证明的要求：不仅概念不严谨，在关键处断链！这好像不是刘老师的水平！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
