昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
引用 寒湘子 的回复内容：
……
我们讲最基本的正弦函数函数的定义：一个角的正弦是直角三角形中角的对边与斜边的比例，当角度变化，角的正弦值也随之变化，当角度为自变量x时，正弦值为y，记为y=sin(x),称为正弦函数。
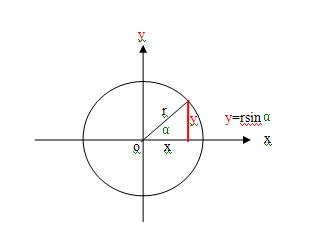
1、如下图，角α的6个三角函数是
sinα=y/r
cosα=x/r
tgα=y/x
……
2、这样正弦函数的定义式应该是：
y=rsinα 就是 对边y=斜边r×正弦值sinα
3、在单位圆中，斜边r=1，这样正弦函数的定义式应该是
对边y=斜边1×正弦值sinα
4、如果是半径r=2的园，那么正弦函数应该是
对边y=斜边2×正弦值sinα
5、如果是半径r=3的园，那么正弦函数应该是
对边y=斜边3×正弦值sinα
6、那寒湘子凭什么说“y=sinα是正弦函数，y=2sinα还真不是正弦函数”？？？
我们再来看665楼刘老师的另一个观点：“1、“函数图像变换”，函数的类别并没有变化。是对数函数，图像变换后还是对数函数；是幂函数，图像变换后，还是幂函数；是正弦函数，图像变换后还是正弦函数，……。”
首先，我们开看“函数图象变换”这个表述，函数变换是一个概念假如函数f(x)通过某一变换T，变换成函数g(u)。可以写成g(u)=T[f(x)]。这样变换有一个例子，即拉普拉斯变换，将时间变量t的线性微分方程，变成s变量的代数方程。显然不能讲函数的类别没有变化。
其次，我们来看图象的变换，在Oxyz空间直角坐标系中平行于xOy平面的一个圆倾斜，在xOy平面就变成椭圆，如果用函数表示。圆的方程变为椭圆的方程（这种情况是隐函数）。函数类型算不算变化，当圆立起来变为直线，其函数类别不变化。
上面两种情况，函数类别显然难保证不变！
好了，刘老师讲：我讲的是函数图象变换。怎么变咱不知道。我保证函数类别不变，图象变行不行。
当然可以：一个变量等于常量，在直角坐标系是平行于坐标轴的直线，而在极坐标中就可能是一个圆！
引用 寒湘子 的回复内容：
直角三角形的三条边中两条边的比例关系产生的函数。……所以三角函数就定义了六个三角函数（正弦、余弦、正切、余切、正割、余割）这六个三角函数不是独立的，已知一个角，这六个函数值就同时确定！……
1、如下图，角α的正切函数定义为
tgα=y/x y=xtgα 对边y=临边x × 正切值tgα
2、在单位圆中，临边x=1，这样正弦函数的定义式应该是
对边y=临边1×正切值tgα y=tgα
3、如果是半径r=2的园，那么正切函数应该是
对边y=临边2×正弦值tgα
4、如果是半径r=3的园，那么正切函数应该是
对边y=临边3×正弦值tgα
5、那寒湘子凭什么说“y=tgα是正切函数，y=2tgα还真不是正切函数”？？？
6、所以，在6个三角函数中，都是“边”与“角”的函数关系，都不是“函数值”与“角”的函数关系；
引用 寒湘子 的回复内容：
我们从上面分析可以看出“函数图象变换”是个多么含混的概念，既使如此，要想函数类型保持不变，都是困难的。在上面例子，你看到函数类型（或性质）都已经变了！
请寒湘子回答，下列说法是否有错：
1）定义式y=loga(x)，对数y是真数x的对数函数，那么非定义式y=-3loga(-4x-6)+5，也同样y是x的对数函数；
2）定义式y=sin(x)，函数值y是角x的正弦函数，那么非定义式的y=Asin(ωx+φ)+B，也同样y是时间x的正弦函数；
3）定义式y=(x)^a，幂值y是底数x的幂函数，那么非定义式的y=d(bx+c)^a+e，也同样y是x的幂函数；
那么刘老师的命题就不是真命题，换句话刘老师说的是假话！
我们再来看看刘老师在730楼的观点：“在6个三角函数中，都是“边”与“角”的函数关系，都不是“函数值”与“角”的函数关系”
但刘老师在665楼又说：“正弦函数的映射关系sin( )，其实质是 正弦值=sin( 角)，用语言说正弦函数就是正弦值与角的映射；”
665楼他明确讲：“正弦函数就是正弦值与角的映射”，730楼又说：“在6个三角函数中，...，都不是“函数值”与“角”的函数关系”，正弦函数显然是6个三角函数中的一个，因而必然有“正弦函数不是“函数值”与“角”的函数关系”
这样刘老师自己的论述就自相矛盾了。
三角函数怎么会是边与角的关系？正弦函数是对边和角的关系，还是斜边和角的关系。一个确定，不管边的长短如何，正弦函数的值都是一个。请问正弦函数与单独的三角形的某一边，有一毛钱关系吗？
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
