昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
引用 寒湘子 的回复内容：
这不是我个人的理解，而是数学就是这么个东西。一切必须由“元名”---基本概念，和“元宜”---基本关系导出。无论是算数、代数、还是几何！这种方法叫做“公理体系”。究其本质“正弦函数”和“对数函数”是“基本的初等函数”，定义的就是最简单的形式，至于其余演算，那是变换的问题。本身对于指定自变量x都不可以简单的说是“正弦函数”或“对数函数”除非对基本自变量x满足其运算规则！“三角函数”则不同它是涉及基本三角函数（正弦、余弦、正切、余切、正割、余割）代数式都可以称为“三角函数”。在电工领域，不是严格使用正弦函数这个概念，我们一般讲正弦波，不能因为有正弦两个字就是正弦函数，但是在归一化处理时将相位角作为自变量（而不是时间t），这时才是正弦函数。所以在电工里正弦波形只有在上述情况下才是正弦函数。
1、寒湘子说，“将相位角作为自变量（而不是时间t），这时才是正弦函数。 ”；
2、寒湘子又说，“在电工领域，不是严格使用正弦函数这个概念，”；
3、寒湘子又说，“究其本质“正弦函数”和“对数函数”是“基本的初等函数”，定义的就是最简单的形式，至于其余演算，那是变换的问题。本身对于指定自变量x都不可以简单的说是“正弦函数”或“对数函数”除非对基本自变量x满足其运算规则！”
4、下来我们看看，寒湘子究竟错在哪儿了？
5、寒湘子说，“y=sin(x)是正弦函数”，“y=2sin(x)还真不是正弦函数；”
6、我们还是把函数的图贴出来讲，直观一点：
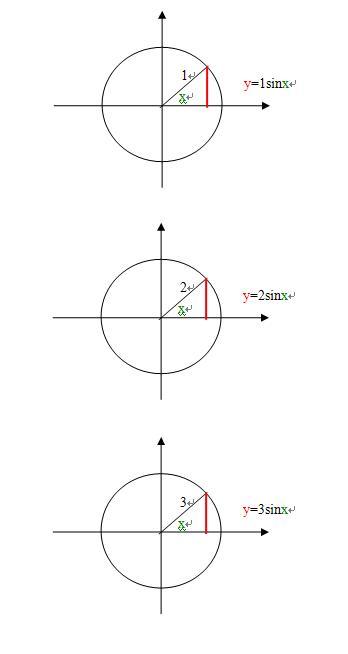
1）大家看下图，定义式y=sin(x)是正弦函数，x是角，y是正弦值（也是对边对边），函数映射关系是sin( )；
2）y=2sin(x)、y=3sin(x)、……，x是角，y是对边，1、2、3是斜边，sin(x)是正弦值，函数映射关系是sin( )；
3）定义式是角的正弦值sin(x)是角x的正弦函数，那么对边2sin(x)、3sin(x)、……，是角x的正弦函数吗？
4）对边2sin(x)、3sin(x)、……，与正弦值sin(x)之间是什么函数？是正比函数，就是说正弦值sin(x)怎么变化，对边就怎么变化，
a、正弦值sin(x)是零，对边也是零；
b、正弦值sin(x)正的最大，对边也是正的最大；
c、正弦值sin(x)是负的最大，对边也是负的最大；
d、就是说“正弦值sin(x)怎么变化，对边2sin(x)、3sin(x)、……就怎么变化”，正弦值sin(x)是角x的正弦函数，对边2sin(x)、3sin(x)、……也是角x的正弦函数；
8、我们看看下面的图
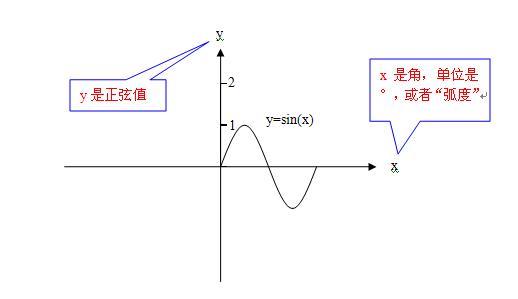
1）y=sin(x)是正弦函数，x是“角”，y是正弦sin(x)；
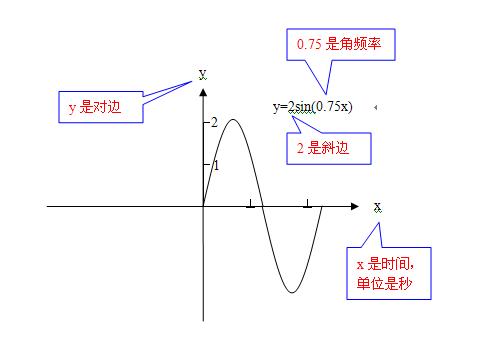
2）y=2sin(0.75x)还是正弦函数吗？看波形确实是正弦函数的波形没有变；
3）y=2sin(0.75x)，x是“时间”，不是“角 ”；
4）但是“0.75x”是角，说以寒湘子说y是“0.75x”的正弦函数，y不是“x”时间的正弦函数；
5）“0.75x”是角，与时间x是什么关系？
a、“0.75x”是角，与时间x是正比函数关系！
b、时间x等于零，“0.75x”角就是零；
c、时间x等于10，“0.75x”角就是7.5弧度；
d、时间x等于100，“0.75x”角就是75弧度；
e、有什么样的时间，就有什么样的角，什么样的角对应什么样的时间，y是“0.75x”的正弦函数，y当然也是“x”时间的正弦函数；
f、所以横坐标x的单位可以标注“秒”，也可以标注“弧度”，它们之间可以互换算！
g、所以横坐标x的单位可以标注“秒”，也可以标注“弧度”，它们之间可以互换算！图像的波形不会因标注“秒”，或者标注“弧度”，有什么变化？
10、通过以上分析，我们可以大胆地说，
1）定义式y=loga(x)，对数y是真数x的对数函数，那么非定义式y=-3loga(-4x-6)+5，也同样y是x的对数函数；
2）定义式y=sin(x)，函数值y是角x的正弦函数，那么非定义式的y=Asin(ωx+φ)+B，也同样y是时间x的正弦函数；
3）定义式y=(x)^a，幂值y是底数x的幂函数，那么非定义式的y=d(bx+c)^a+e，也同样y是x的幂函数；
11、我们这样说对吗？
1）寒湘子认为是违背定义；
2）我认为是应用了定义；
3）因为有“基本初等函数的定义”，所以才有“变换所得的非定义式的同类函数”；
4）是寒湘子的思维逻辑出了问题！
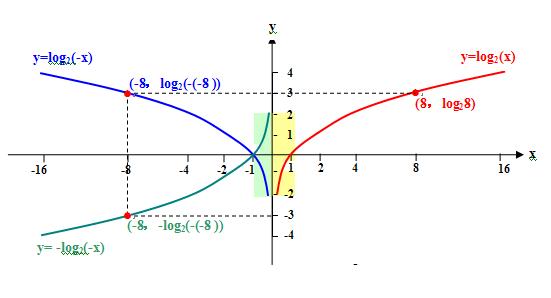
按照刘志斌的乱弹逻辑：横坐标(-8)和横坐标(-(-8))都在y轴左侧？？！
中学生都知道：自变量的任一取值x所对应f(x)曲线上的点的坐标为(x，f(x))，当自变量取值为前者的相反数“-x”时对应的坐标为(-x，f(-x))。即函数值符号之“括弧”中的值本该是对应的自变量值。例如，自变量值取8，则对应“括弧”中的值为8 ，即“f(8)” ；自变量值取“-8”，则对应“括号”中的值为-8，即“f(-8)”……
但是，在刘志斌自创的“刘理论”中，却出现了自变量取值x=“-8”所对应曲线上的点的坐标却不为“(-8，f(-8))”！而是反其道而行之！
刘志斌将其胡搅成“(-8，f(8)” ! 刘“大师”总是热衷于与正统理论相抵触！
刘老师讲：“我真的不敢恭维寒湘子，寒湘子大话连篇，帽子满天飞，被一个小小的数学题难倒了，真不可思议！”
给人扣帽子的大师，恐怕非刘老师莫属！
刘老师，口口声声我不懂对数函数，甚至这个小小的数学题也不能解，竟敢和刘老师这样的大师论战。我真的让刘老师很不舒服！
我觉得花瓣的见解比须眉要真诚，论坛早就酸腐了。是谁大话连篇，早有公论！
我们看看惊人骇俗的论断：
“矢量控制变频器是谎言！”
“异步电动机的滑差转矩曲线是幂函数！”
“拉氏变换的s变量是时间变量”
如果不理解可以学习，但是拒绝学习的人，就根本无可救药！
子曰:“学而不思则惘，思而不学则殆”，思考和学习必须相辅相成。对于乱思不学的人，必然走火入魔。
为了让走火入魔的人清醒，有必要来一一驳斥其荒谬逻辑！
665楼，刘老师讲：“正弦函数的映射关系sin( )，其实质是 正弦值=sin( 角)，用语言说正弦函数就是正弦值与角的映射；”
首先，我们来看看刘老师的表述：正弦函数就是正弦值与角的映射。
按照刘老师的定义，正弦函数是一种映射，映射是一个集合的元素，和另一个集合的元素的一种关系。这样映射一定要指明集合元素了。刘老师讲这两个集合的元素：一个是正弦值，一个是角度。这样问题来了：为了说明正弦函数，就必须知道正弦值和角的关系；而要知道正弦值又必须通过正弦函数由自变量角度求得。
这样就构成自我表述的逻辑循环。这样的同语表述在数学上不可能成为一个定义。
刘老师给出的正弦函数的表达是：正弦值=sin( 角)，一般的理解只能是正弦值由角的正弦函数求出。可见其语言表述也是反的！
所以没有人可以由刘老师的定义，求出正弦值。也没有人可以从刘老师的定义中了解什么是正弦函数。
请问30度角的正弦值是多少？你不能根据刘老师的定义求出！
这个表述的荒唐之处可以看出了。因为初中生如果你告诉他什么是正弦，求30度角的正弦是很简单的。但是跟刘老师学习正弦函数后，竟然不能够求，岂不是怪事！
三角函数与欧几里得几何学直接相关。是由直角三角形的勾股定理，和直角三角形的三条边中两条边的比例关系产生的函数。因为3条边选两条边的排列有3*2=6个，所以三角函数就定义了六个三角函数（正弦、余弦、正切、余切、正割、余割）这六个三角函数不是独立的，已知一个角，这六个函数值就同时确定！
三角函数先是定义锐角的三角函数，之后推广到任意角。
我们讲最基本的正弦函数函数的定义：一个角的正弦是直角三角形中角的对边与斜边的比例，当角度变化，角的正弦值也随之变化，当角度为自变量x时，正弦值为y，记为y=sin(x),称为正弦函数。
根据这个定义：
30度角的正弦，因为对边为斜边的一半，所以根据定义就是0.5。
而45度角的正弦，由直角三角形三边关系，和正弦函数定义，其正弦值就是根号2的一半。
而按照刘老师的定义我们什么都不知道！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
