昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
引用 寒湘子 的回复内容：
loga(x)+loga(-x)不是偶函数，loga(x)-loga(-x)也不会是奇函数！因为当x值为正（负），-x必为负（正），loga(x)和loga(-x)总有一个是无意义的。其和或差也就无意义。
1、“ loga(x)和loga(-x)总有一个是无意义的。其和或差也就无意义。”，寒湘子的这个观点很明确；
2、如果这个观点正确，此题无解！
3、我的观点是：
1）如果是做算术 4－（ ）=？，因为（）不确定，此题无解；
2）函数的运算，是在其定义域上的运算，在函数的定义域上，该函数有意义存在，不在该函数的定义域上该函数不存在，这样
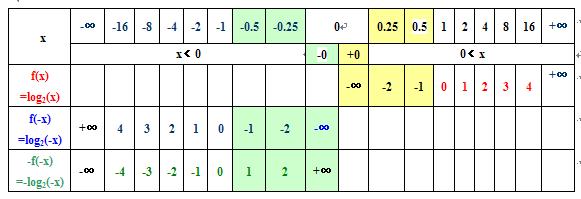
在x＞0的区间上，-f(-x)不存在，只有f(x)存在，所以 f(x)-f(-x)=f(x)；
在x＜0的区间上，f(x)不存在，只有-f(-x)存在，所以 f(x)-f(-x)=-f(-x)；
3）所以这个题目正确，有唯一的解。
引用 寒湘子 的回复内容：
……不要因为我讲g(x)=f(x)+f(-x)是偶函数，h(x)=f(x)-f(-x)是寄函数，你就可以随便推广，因为大家知道我这么说暗含f(x)和f(-x)都有意义，即x定义域是关于原点的对称区间。但是你不懂，所以就乱讲了，……
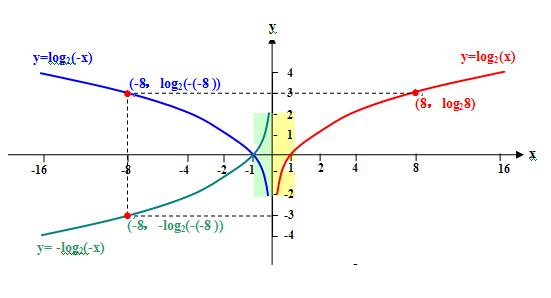
1、g(x)=f(x)+f(-x)，因为f(x)图像与f(-x)图像以y轴为对称，所以是偶函数；
因为 g(x)=f(x)+f(-x)
g(-x)=f(-x)+f(x)
所以 g(x)=g(-x)，满足偶函数的条件；
2、h(x)=f(x)-f(-x)，因为f(x)图像与-f(-x)图像以原点为对称，所以是奇函数；
因为 h(x)=f(x)-f(-x)
h(-x)=f(-x)-f(x)，-h(-x)=f(x)-f(-x)，
所以 h(x)=-h(-x)，满足奇函数的条件；
3、g(x)和h(x)的定义域均为{x＜0，x＞0}
4、g(x)和h(x)的值域均为R；
5、这样h(x)/x＜0，x的范围是，-1＜x＜0，0＜x＜1；
如图
引用 寒湘子 的回复内容：
……对于x<0，f(x)没有定义。同样对于x>0，f(-x)也是没有定义的。从而f(x)-f(-x)总有一个是不确定的。根据题目只能判定在负无穷到0区间上f(-x)是减函数，并且x=-1时f(-x)=0!而不能求出题目要求的x值范围！...
1、做算术运算 4-( ) =?，( )是多少？不确定，是1得3，是2得2，……，此题无解；
2、“对于x<0，f(x)没有定义。同样对于x>0，f(-x)也是没有定义的。从而f(x)-f(-x)总有一个是不确定的。”，这句话错误，正确的说法是“对于x<0，f(x)没有定义。同样对于x>0，f(-x)也是没有定义的。从而f(x)-f(-x)总有一个是不存在的。”
3、如果是不确定，像1那样，那是无解；
4、如果是函数不在定义域上，此函数不存在，很确定，就是不存在，那是有解的！
1）x>0，f(-x)也是没有定义的，不存在，所以 f(x)-f(-x)=f(x)；
2）x<0，f(x)没有定义，不存在，所以 f(x)-f(-x)=-f(-x)
引用 寒湘子 的回复内容：
如果是函数不在定义域上，此函数不存在，很确定，就是不存在，那是有解的！
1）x>0，f(-x)也是没有定义的，不存在，所以 f(x)-f(-x)=f(x)；
……
如果诚如刘老师所说：
在1）的情况下我们必然有f(-x)=0；
……
1、 说“在1）的情况下我们必然有f(-x)=0”；”这句话是错的，f(-x)不在定义域上，不存在，怎么能有f(-x)=0呢 ？
2、很明显，寒湘子在用诡辩术和我辩论！
3、这和寒湘子说的“……错了改了就好，谁没有错呢？为什么为了为一个错误辩解，而导致更多的错误呢？何苦呢？”，不相吻合！
3、g(x)和h(x)的定义域均为{x＜0，x＞0}
4、g(x)和h(x)的值域均为R；
第3点显然是错的。g(x)和h(x)的定义域可以是{xI-a<x<-b且b<x<a,其中a>b>或=0}的任何形式，当然全闭区间或对称半开半闭区间也是成立的，而刘老师给出的定义域x必不为0！
第4点显然也是错误的。如f(x)=sin(x)+cos(x)于是有f(-x)=sin(-x)+cos(-x)=-sin(x)+cos(x)
所以g(x)=f(x)+f(-x)=2cos(x),h(x)=f(x)-f(x)=2sin(x)
可以看出g(x)是偶函数而h(x)是奇函数。但是两者的值域都是绝对值不大于2的闭区间，而不是整个实数集R!
引用 寒湘子 的回复内容：
h(x)=f(x)-f(-x)，因为f(x)图像与-f(-x)图像以原点为对称，所以是奇函数；
因为 h(x)=f(x)-f(-x)
h(-x)=f(-x)-f(x)，-h(-x)=f(x)-f(-x)，
所以 h(x)=-h(-x)，满足奇函数的条件；
这同样与f(x)图像与-f(-x)图像以原点为对不对称无关！
1、因为“ f(x)图像与-f(-x)图像以原点为对称”，才有 ：
h(x)=f(x)-f(-x)
h(-x)=f(-x)-f(x)，-h(-x)=f(x)-f(-x)，
所以 h(x)=-h(-x)，
2、如果不知道“ f(x)图像与-f(-x)图像以原点为对称”，怎么知道
h(x)=f(x)-f(-x)
h(-x)=f(-x)-f(x)，-h(-x)=f(x)-f(-x)，
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
