昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
引用 wanggq 的回复内容：
刚表扬了刘志斌知道他把对数函数搅到2、3象限之行为是错误的了，知道把y轴左侧的曲线标注的“logax”或“lgx”字样删掉了。
车转身，刘志斌这犟牛又搅回去了再次胡说他刘志斌在y轴左侧的曲线标注对数函数标志性符号“log”是“对的”，为他刘志斌的荒谬错误招魂！
1、基本初等函数中，对数函数的定义式是y=loga(x)，分a＞1、a＜1两种情况，其图像在1、4象限，如图
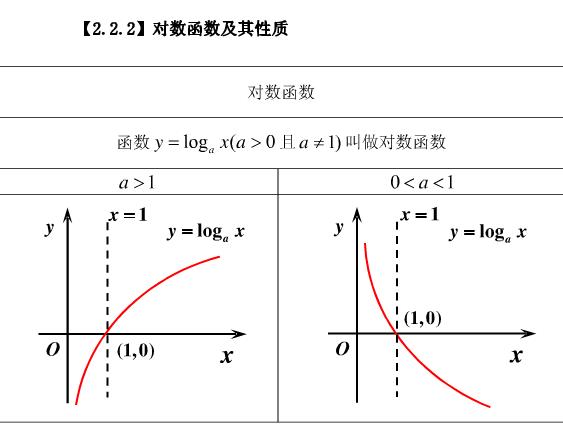
2、基本初等函数的解析定义式为，y=loga(x)，分a＞1或a＜1；
3、基本初等函数的定义域是x＞0，值域是R；
4、基本初等函数图像变换后，不再是定义式的对数函数，例如以y轴对称平移所得对数函数的解析式是y=loga(-x)，分a＞1或a＜1，定义域为x＜0，图像在2、3象限， 值域-R！
5、基本初等函数图像变换后，只是不是定义式的对数函数，y=loga(-x)还是对数函数；
6、 wanggq 睁着眼说瞎话、掩着耳盗铃，惹人笑之！！！
引用 wanggq 的回复内容：
……这个图上的内容是：对数函数的图象在1、4象限！不支持刘志斌把对数函数搅到2、3象限！……
1、看看高中数学知识点的总结，是怎么说的：
2、利用基本初等函数图像的变换作图，做出来的图是什么函数的图？当然还是同类函数的图像，不可能是别类函数；
3、要准确记忆各种基本初等函数的图像，由此变换做出同类函数的图像；
4、例如，求作对数函数log2(-x)的图像，你只要把基本对数函数log2(x)的图像以y轴对称变换得之，
5、当然还可以在上述以y轴对称变换后，在继续以x轴对称变换之后，继续向上平移3、相左平移4、y轴拉伸5、x轴压缩6， 最后得到对数函数：
y = - 5 log2 ( - 6x - 4 ) + 3
引用 wanggq 的回复内容：
这个图上的内容是：对数函数的图象在1、4象限！不支持刘志斌把对数函数搅到2、3象限！
也就是说：对数函数只能在y轴的右侧，而不能在左侧！刘志斌把对数函数画在y轴左侧是错误的！
1、基本初等函数讨论时，都有严格的定义，举例说
对数函数的定义式是y=loga(x) a＞0或a＜0 定义域是x＞0，图像在1、4象限；
2、那么一般对数函数 的图像，都可以通过基本初等对数函数的图像变换而得，例如
y=loga(x) ，通过：
①以y轴为对称变换得y=loga(-x)
→②以x轴为对称变换得y=-loga(-x)
→③x轴压缩⒊倍得y=-loga(-3x)
→④y轴拉伸4倍得y=-4loga(-3x)
→⑤y轴向上平移5个单位得y=-4loga(-3x)+5
→⑥x轴右平移6个单位得y=-4loga(-3x-6)+5
3、我么看到基本初等对数函数y=loga(x) ，是研究一般对数函数y=-4loga(-3x-6)+5的基础，它支持了一般初等对数函数y=-4loga(-3x-6)+5的变换求解的过程；
4、根据基本初等函数的定义， wanggq 和寒湘子认为y=loga(x)是对数函数，而y=-4loga(-3x-6)+5就不是对数函数了，这是个错误的理解；
5、基本初等函数的定义式，只是该类函数的一个特定式，是最基本的特定式，通过它的变换，可以获得该类函数的一般式；
6、举例说，寒湘子认为y=sinx是正弦三角函数，而由y=sinx的图像变换所得的y=2sinx就不是正弦三角函数；
7、举例说，我们常常说的正弦交流电压 u=510sin(314t-120°）v，就是一个正弦函数，它是由基本正弦函数y=sin(t) ，通过：
①t轴压缩314倍得y=sin(314t)
→②t轴右移120°得y=sin(314t-120°)
→③t轴拉伸510得y=510sin(314t-120°)
8、wanggq 和寒湘子说y=510sin(314t-120°)不是正弦函数，只有y=sin(t)是正弦函数，是不理解基本初等正弦函数定义式只是个特定意义的研究对象；
4、根据基本初等函数的定义， wanggq 和寒湘子认为y=x^a是幂函数，而y=2sinx就不是幂函数了，这是个错误的理解；
5、基本初等函数的定义式，只是该类函数的一个特定式，是最基本的一个讨论特定式，通过它的变换，可以获得该类函数的一般式；
6、举例说，wanggq和寒湘子认为y=x^a是幂函数，而由y=x^a的图像y轴拉伸变换所得的y=2x就不是幂函数，是错误的！
7、举例说，幂函数y=5(2x+3)^2+4，就是一个幂函数，它是由基本幂函数y=x^2 ，通过：
①x轴压缩2倍得y=2x^2
→②x轴左平移3个单位得y=(2x+3)^2
→③y轴拉伸5倍得y=5(2x+3)^2
→④y轴上平移4得y=5(2x+3)^2+4
8、但是wanggq 和寒湘子说y=5(2x+3)^2+4不是幂函数，是错误理解了基本初等幂函数定义式只是个讨论的特定意义式；
11、基本初等函数f(x)，经过图像的对称、平移、拉伸、压缩等变化后，函数的解析式变成
y=af(bx+c)+d，其中有一个东西没有变，这就是f( )没有变，f( )就是该类函数的基本函数映射关系；
12、举例说，y=-4loga(-3x-6)+5的基本函数映射关系是loga( )，没有变，它就是该类函数的特征，叫做对数函数；
13、举例说， u=510sin(314t-120°) 的基本函数映射关系是sin( )，没有变，它就是该类函数的特征，叫做正弦函数；
14、举例说， y=5(2x+3)^2+4的基本函数映射关系是( )^a，没有变，它就是该类函数的特征，叫做幂函数；
15、基本初等函数，只是该类函数中一个最基本的特定的讨论定义式！
引用 wanggq 的回复内容：
……“求(f(x)-f(-x)) /x<0时x的范围”其“f(x)”、“f(-x)”皆表示“函数值”。……
1、函数图像的变换，是学生学习函数图像的难点，…也是学生易混和不易掌握的基本概念；
2、函数y=f(-x)的图像，是已知函数y=f(x)的图像沿y轴翻折180°而得到的，即函数y=f(-x)的图像与已知函数y=f(x)的图像以y轴为对称；
3、当一个函数f(x)满足条件f(x)=f(-x)时，其图象以y轴为对称；
4、很多同学把“2”、“3”混淆起来，“2”、“3”的区别是，“2”是两个函数f(x)、f(-x)的图像以y轴为对称函，“3”是一个数的图像以y轴为对称必须满足的条件是f(x)=f(-x)；
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
