昨天一道高中的数学题，我竟然不会做了 点击：22294 | 回复：1402
楼主最近还看过
我们都知道，平面直角坐标系里任意一条（纵坐标相依横坐标成单值对应变化的点的集合）曲线都是一个“函数”。
把曲线标注成“y=f(x)”或者简单的标注成“f(x)”都是可以的！
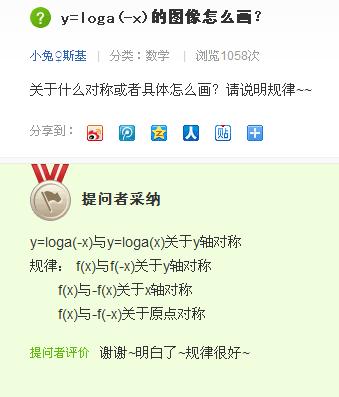
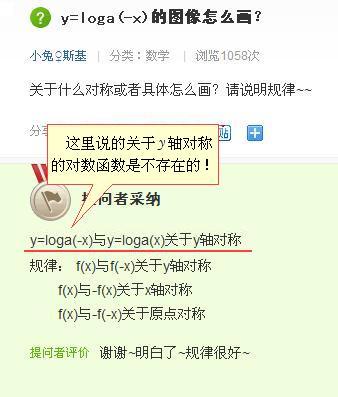
所以，刘志斌就把他的“错误对数函数”曲线改标为“f(x)”、“f(-x)”、
“-f(-x)”： （下图就是从刘志斌帖子里复制下来的图片）
请注意：我是说刘志斌这曲线图上的标注“y=f(x)”、“f(x)”是没有错的！这说明刘志斌也曾经意识到y轴左侧曲线上标注“y=f(-x)=loga(-x)”、“y=-f(-x)=-loga(-x)”的错误！
如果刘志斌没有意思到y轴左侧没有“x的对数函数”刘志斌就不会删改当初的标注“y=f(x)logax”、“y=f(-x)=loga(-x)”、“y=-f(-x)=-loga(-x)”!
刘志斌也把帖子的文字做了删改，但是，刘志斌既要删除“把柄”，又要顽固坚持用他的“唯一仅有对数函数才符合题目‘f(x)在0到正无穷大是增函数，
f(1)=0’的条件要求”这一错误“刘理论”来荼毒青年！所以，刘志斌仍然保留了在文字上描述y轴左侧“曲线”为：“2) 那么函数f(-x)=loga(-x)，a＞1，定义域为0到负无穷大是减函数；”
把在图片中y轴左侧曲线上标注的对数函数标志性符号“loga(-x)”删掉，改用文字描述该曲线的错误是同样的！刘志斌自以为不在曲线上直接标注对数标志性符号“loga(-x)”就可以掩盖他的荒谬，刘志斌这种“掩耳盗铃”式的行径真叫人笑话！
最初，刘志斌是一口咬定说：“符合f(x)在0到正无穷大是增函数，f(1)=0,这种条件的只有对数函数”还用非常尖酸又刻薄的言语跟对手<烟雨朦朦>激烈的争辩了很多时候，经过争辩也从对手<烟雨朦朦>的发言中学到了“符合题目条件的函数多得很”的知识，于是刘志斌也把原来理直气壮的咬定“唯一仅有对数”的口气缓和为“可以理解为对数”！
本来题目的题设部分“f(x)在0到正无穷大是增函数，f(1)=0”中只提了两个条件，1、“f(x)在0到正无穷大是增函数”；2、“f(1)=0”。
刘志斌故意将第1个条件硬生生的拆分成仨条件：1) f(x)在0到正无穷大；2) 增函数；3) f(1)=0；
刘志斌的目的很明显：有意把函数的“单调区间”概念搅混成“定义域”概念！
引用 wanggq 的回复内容：
最初，刘志斌是一口咬定说：“符合f(x)在0到正无穷大是增函数，f(1)=0,这种条件的只有对数函数”还用非常刻薄的言语与对手<烟雨朦朦>激烈的争辩了很多时候，经过争辩也从对手<烟雨朦朦>的发言中学到了“符合题目条件的函数多得很”的知识，于是刘志斌也把原来理直气壮的咬定“唯一只有对数”的口气缓和为“可以理解为对数”！
1、这也是造谣！
2、基本初等函数图像中，符合“f(x)在0到正无穷大是增函数，f(1)=0，”这三个条件的只有对数函数”；
3、其它符合f(x)在0到正无穷大是增函数，f(1)=0,这三条件的函数有很多，但都不是基本初等函数定义式的图像；
4、wanggq 能举出第二个符合f(x)在0到正无穷大是增函数，f(1)=0,这三条件的基本初等函数定义式的图像吗？
对数函数是指数函数的反函数！
这个得从“幂概念的推广”给刘志斌讲起！
零指数幂
最初的时候，n个相同因子a的积叫做a的n次幂，写作a^n。这个定义不适合零指数幂，因为把a^0 理解为a自乘0次是没有意义的。所以必须a^0另给定义。
我们知道正整指数幂的除法法则是：
(a^m/a^n)＝a^(m-n) (a≠0)
这个法则在此之前只有在m、n都是正整数，并且m＞n时才能适用。如果
m=n，那么根据这个法则所得到的等式右边就出现了a^0，而等式左边明显等于1。很自然地我们会想到，假如我们规定a^0=1，那么，这个法则在m=n时也就可以适用了。
<紧接№556楼的内容>
负整指数幂
在正整指数幂的除法法则：
(a^m/a^n)＝a^(m-n) (a≠0)
中，如果m＜n，例如m=3，n=5，那么，根据这个法则得到的等式右边便出现了负整指数幂：a^(m-n)＝a^(3-5)＝a^(-2) ；等式左端显然是：
a^m/a^n＝a^3/a^5＝1/a^(-2) 。
很自然地，我们会想到假如规定a^(-2)＝1/a^2 ，那么，这个法则在m＜n时也就能适用了。从这个例子推广到一般情况，为了使上面的法则在m＜n时也能适用，我们给出下面的定义：
任一不等于零的数的负整指数幂等于把幂的指数变号后所得的幂的倒数，也就是
a^(-p)=1/a^(-p) (a≠0，p为正整数)。
分指数幂
在初中已经学过，如果n是大于1的正整数，m是n的整数倍，那么
(这网页上不便编辑数学表达式，只能凑合着理解吧！ 请注意：后边这个n是“根指数”) n√a^m=a^(m/n) 。
如果m不是n的整倍数，在上面等式的右边便出现了分指数幂。例如：m=2，n=3，那么，a^(m/n)＝a^(2/3) 。显然记号a^(2/3)不能用正整数幂的定义来解释，因为把a^(2/3)理解为a自乘“2/3”次是没有意义的，所以必须对a 的分指数幂另给定义。
假如我们规定n√a^m＝a^(m/n) 在m不是n的整倍数时也能适用已有的指数运算法则，我们自然应该把a^(m/n)看成是根式n√a^m的另一种写法。因此，我们给出下面的定义：
正数的正分指数幂表示一个根式，它的根指数是分指数的分母，根底数的幂指数是分指数的分子；也就是
a^(m/n)＝n√a^m (m、n是正整数且a＞0 )
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
