引用 wanggq 的回复内容： 　　　　

……

3)、函数f(x)的自变量在定义域内可取得互为相反的数的值。即函数f(x)的定义域延伸到x＜0的区域。

 　　（这蕴含在题目核心部分“求(f(x)-f(-x))/x＜0 时 x的范围”中的第3个条件可不是老王自己添加的，而是老王用慧眼从原题目的字里行间看出来的！）

1、wanggq用慧眼把-x看成负数，把loga(-x)看成负数的对数，大喊无意义！

2、wanggq又用慧眼把“求(f(x)-f(-x))/x＜0 时 x的范围”中的f(x)、f(-x)看成，函数f(x)的自变量在定义域内取得互为相反的数的函数值。

3、wanggq的慧眼，使得楼主的题目变成无知无解的错题，附和了寒湘子1楼的发言，寒湘子当然要知恩图报，不惜勇做把-x看成负数的人，

4、wanggq的慧眼，说明wanggq比出题目的人还要懂函数，出题目的人一定不知道-x是负数，

loga(-x)是负数的对数，……，所以才会出“错”题！

5、我把wanggq和寒湘子好有一比，就像两个把自己耳朵掩住，心里想，这下谁也听不见就好像谁也不知道-x也会是正数，所以大着胆子大模大样旁若无人地盗铃的“伙伴”一样！

引用 wanggq 的回复内容：   　　　

……原题目的解就不是“唯一”的！而是在一个限定范围内的“解集”！这个“解集”中的元素多得数不清，但是，这个“解集”却偏偏就是不包含刘志斌胡搞出的俩解！（即不包含刘志斌的“对数型”解，和“直线型”解）

1、看得出， wanggq 为他能对主楼题目解得的“解集”中的元素多得数不清，而洋洋得意！

2、wanggq 遗憾的告诉大家，他的“解集”中的元素多得数不清，却偏偏就是不包含刘志斌胡搞出的俩解！

3、其实wanggq 聪明，wanggq 的儿子更聪明，翻开数学作业，别人一道数学题只有一个答案，wanggq 的儿子做的数学题，都会有好几个正确答案！

……哈哈！

关于函数f(x)和函数f(-x)：

1、函数f(x)和函数f(-x)是两个函数， 因为函数f(-x)的对应关系是f(-())， 而函数f(x)的对应关系是f()，f(-())比f()，多了一个“对自变量x求反”运算；

1）举例说，对数函数logax和对数函数loga(-x)，对数函数loga(-x)对自变量x有一个求反的运算；

2）当x是负数时，-x就是一个正数；

3）这样对数函数loga(-x)的定义域就是x＜0，-x是个正数；

4）而对数函数logax的定义域是x＞0，x是个正数；

5）所以函数loga(-x)的图像在3、4象限，而函数logax的图像在1、2象限；

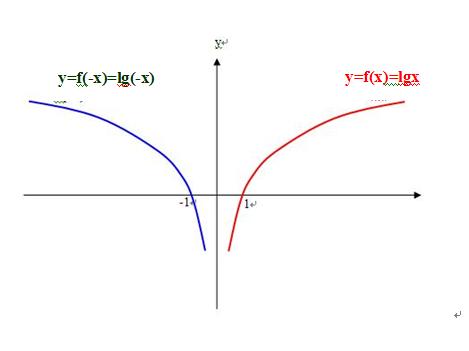
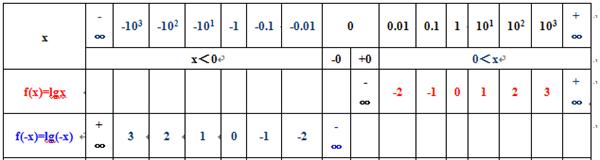
2、函数f(x)和函数f(-x)是两个相关函数， 因为函数f(-x)的对应关系是f(-())， 而函数f(x)的对应关系是f(  )，f(-())和f()都有共同的f(  )；

1）举例说，对数函数loga(x)和对数函数loga(-x)，都是对数函数，都有loga( )；

2）因为负数没有对数，或者说真数只能是正数，所以loga(x)的定义域是x＞0；

3）因为负数没有对数，或者说真数只能是正数，所以loga(-x)的定义域是x＜0,，-x是正数；

4）所以对数函数loga(-x)的图像在3、4象限，而对数函数logax的图像在1、2象限；

3、对于一个任意的有确切定义的已知 函数f(x)， 就一定有一个函数 f(-x)与之对应存在；

1）举例说，已知对数函数y=lg(x)在0到正的无穷大区间上；

2）就一定有对数函数y=lg(-x)在0到负的无穷大区间上；

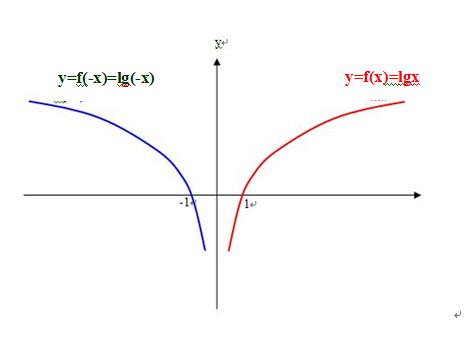
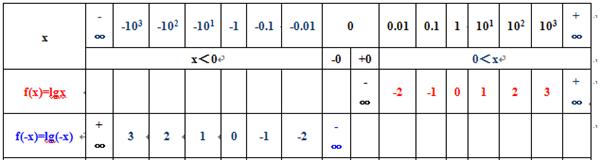
3）举例说，已知幂函数y=(x)^2，在(-∞，+∞)上；

4）就一定有幂函数；y=(-x)^2，在(-∞，+∞)上；

5）因为y=(x)^2=(-(-x))^2以y轴为对称，又因为(x)^2=(-x)^2，(x)^2图像与(-x)^2图像重合，所以幂函数y=(x)^2是个偶函数，幂函数y=(-x)^2也是个偶函数；

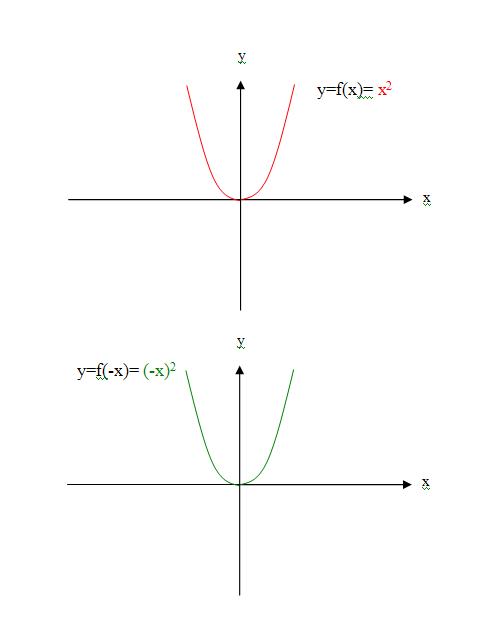
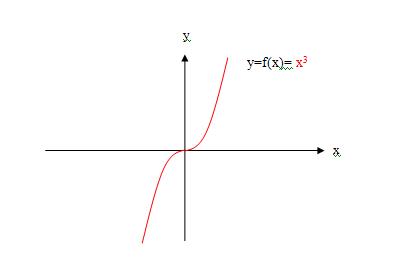
6）举例说，已知幂函数y=(x)^3，在(-∞，+∞)上；

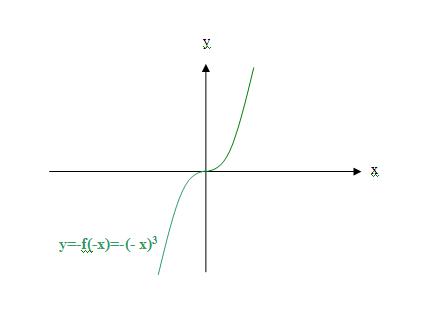
7）就一定有幂函数；y=(-x)^3，在(-∞，+∞)上；

8）因为y=(x)^3=-(-x)^3以y轴为对称，因为(x)^3=-(-x)^3，图像(x)^3与图像-(-x)^3完全重合，所以幂函数y=(x)^3是个奇函数，幂函数y=-(-x)^3也是个奇函数；如图

4、由于有以上函数基础知识存在， 所以出题的人， 才会出主楼这样的题目， 他只需要告诉已知函数f(x)的情况，做题的人自然会求得函数f(-x)、f(x)-f(-x)；

5、由于wanggq和寒湘子，没有上述函数基础知识，对函数f(x)、f(-x)的关系乱作解释，给主楼题目解出了无数多个正确的解，所以无知是错误和谎言之源！！！或者说错误和谎言欺骗的是无知者！！！或者说无知是错误和谎言得以传播的动力 ！！！

6、我们看到，无知的wanggq时不时的搬出“正统大学教材”一些零碎章节的内容截图，却能堂而皇之的把它歪曲成“错误和谎言”，让人们亲身体会到错误与谎言往往是打着科学、技术的幌子欺骗无知者，捞取不义之财！

7、wanggq是怎么堂而皇之的把正确的知识歪曲成“错误和谎言”的呢？

1）在研究偶函数图像以y轴为对称这个性质时，教材中有这样一段叙述

函数y=x^2的图像关于y轴是对称的，我们把具有这种特征的函数叫做偶函数。f(x)是偶函数的标志是：当自变量x取一对互为相反数的值时，函数的值不变，就是f(x)=f(-x)。

如图：

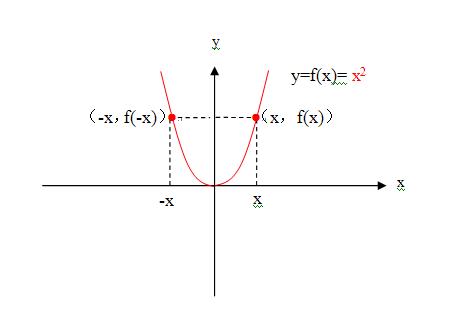
2）根据教材的论述，我们同样可以得到：

函数y=(-x)^2的图像关于y轴是对称的，我们把具有这种特征的函数叫做偶函数。f(x)是偶函数的标志是：当自变量x取一对互为相反数的值时，函数的值不变，就是f(x)=f(-x)。

如图：

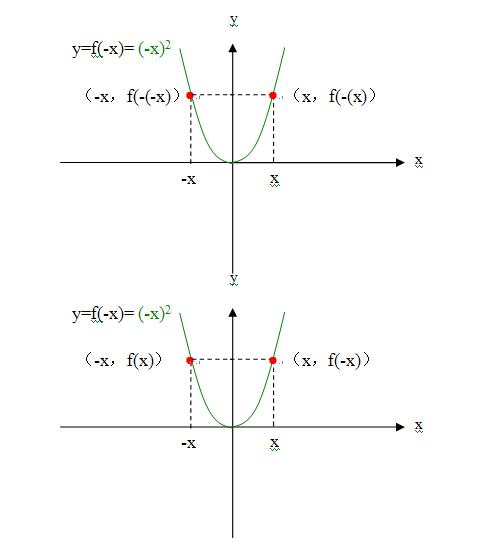
3）这样我们知道函数y=x^2是偶函数，那么函数y=(-x)^2也是偶函数，也就是说，当函数f(x)是偶函数时，一定有函数f(-x)也是偶函数，它们的图像以y轴为对称，以y轴对折时完全重合，函数f(-x)自变量-x对应的函数值f(x)与函数f(x)自变量x对应的函数值f(x)重合；如下图

3）这样我们得到这样一个结论，偶函数时，函数f(x)与函数f(-x)两个都是偶函数，其图像以y轴为对称，以y轴对折时完全重合；

4）如果已知函数f(x)不是偶函数，它的图像，与f(x)相关的函数f(-x)的图像也是以y轴为对称，以y轴对折时，完全重合；

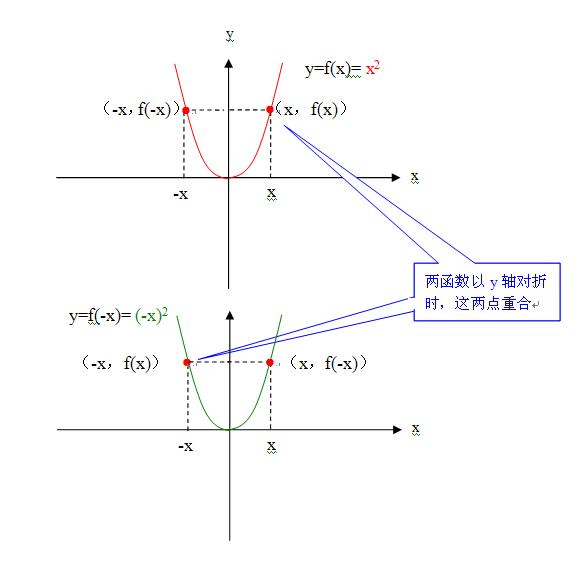
5）wanggq是怎么堂而皇之的把正确的知识歪曲成“错误和谎言”的呢？如截图

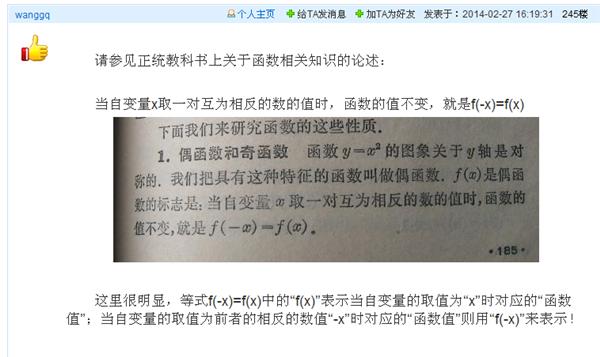
wanggq说，“请参见正统教科书上关于函数相关知识的论述：……当自变量x取一对互为相反的数的值时，函数的值不变，就是f(-x)=f(x) ，……这里很明显，等式f(-x)=f(x)中的“f(x)”表示当自变量的取值为“x”时对应的“函数值”；当自变量的取值为前者的相反的数值“-x”时对应的“函数值”则用“f(-x)”来表示！

wanggq以此为据，认定主楼题目“f(x)在0到正无穷大是增函数，f(1)=0，求（f(x)-f(-x)）/x<0时x的范围”中，f(-x)是已知函数f(x)图像上“自变量取相反数值“-x”时对应的“函数值”！

wanggq以此为据，认定主楼题目“f(x)在0到正无穷大是增函数，f(1)=0，求（f(x)-f(-x)）/x<0时x的范围”中，已知函数f(x)的定义域必然是（-∞，+∞）……

刘老师：请注意我在跟wanggq贴时，我讲得很清楚，我并不确认你有过负数的对数函数的讲法。loga(-x)并不意味是负数的对数函数。因为当x本身是负数，上述函数是有意义的。

只是我顺着wanggq的话题，多讲了一句，实际在复变函数里负数的对数函数是很有意思的。只不过根据题目上上下文。应该是在实函数范围讨论。

这个题目很久了，有点厌倦，找个有趣的题目讨论吧，怎么样，刘老师?

　　寒湘子被刘志斌的胡搅给唬住了！赶紧的与老王划清界线！寒湘子招架不住刘志斌的恶毒诋毁的打击，你寒湘子干脆就撤退算了吧！

　　记号“f(-x)”原本是人们在研究讨论函数奇偶性时引用的一个函数值记号。请注意，“f(-x)”是以所研究讨论的函数的定义域内有“互为相反数（x和-x）”为前提条件而存在的！

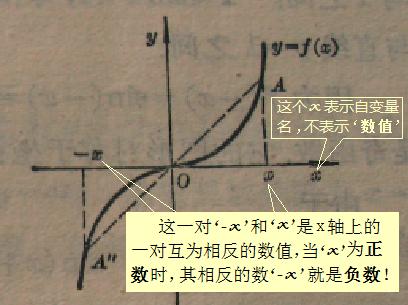
　　再摘取教科书上有关自变量取一对互为相反数(x和-x)分别对应函数值f(x)和函数值f(-x)的插图内容供大家参考：

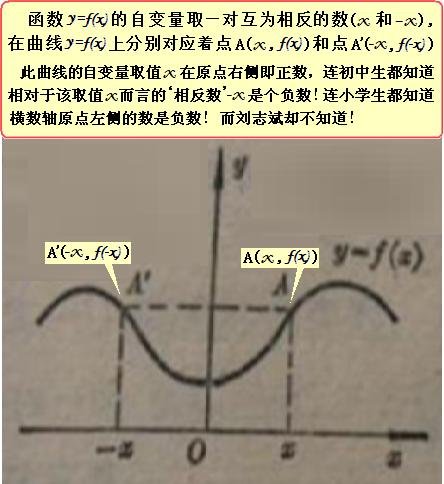
　　相对于自变量在原点右侧的某一取值x (正数)而言的相反数‘-x’ 当然是负数啦！连小学生都知道横数轴原点左侧的数是负数！而刘志斌却不知道！

　　x可以代表函数定义域内任意的某一自变量值（既可以代表负数或零，也可以代表正数） 如上图：x在原点右侧，代表的是某一正数，其相反数“-x” 在原点左侧当然是负数啦！难道这还有疑问吗？！

　　难道刘志斌还弄不懂这一对互为相反的数值‘x’ 和‘-x’，当其中的‘-x’ 处在原点左侧时‘-x’即表示负数 ？！

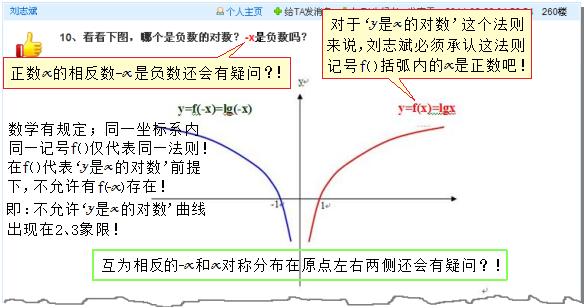
　　一对函数值记号“f(x)” 和“f(-x)” ，其括弧中的内容“x” 和“-x” 代表自变量所取的任意一对互为相反的数值。其中一个自变量值“-x”的“-”号代表的是相对于另一个自变量值“x”而言的‘取反’，并不是如刘志斌瞎胡搅的对应法则f( )内又嵌入另一层对应法则“相对于‘-x’自身再次取反”！

　　请注意：“f(x)” 和“f(-x)” 的法则是同一个法则，其记号都是同一个“f( )”！具体代表的法则并不因其括弧中内容(x 或-x)而改变！

　　但刘志斌却自作聪明的把这一对函数值其中“f(-x)”的法则记号胡搅成：“f(-())”！正统数学理论里是没有这一怪记号的！欲知嵌套的对应法则记号请参阅后述<复合函数>的相关内容！

　　刘志斌为了掩盖自己在“自变量取一对互为相反数(x和-x)”这一问题上所犯的荒谬错误，竟然不惜勇做把正数x的相反数-x看成正数的人！

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

　　题目核心部分那个不等式‘(f(x)-f(-x))/x＜0’中的函数值记号f(x)和f(-x)代表的是同一个函数当自变量取互为相反的数时分别所对应的函数值。

　　而对数函数f(x)=logax 的定义域内根本不存在“互为相反的数”，对数函数的值域内又哪来什么“f(-x)” ？！刘志斌却荒谬的认为题目所设的f(x)就是对数函数。

　　刘志斌为了掩盖自己对f(-x)认知上的谬误，竟然将f(-x)括弧中自变量的数值‘-x’的‘-’负号曲解为：“相对于‘-x’自身再次取反”。使原本只是相对于f(x)括弧中自变量数值x而言的相反数-x，被刘志斌胡搅成双重的取反“-(-x) ”！给原点左侧的负数披上了一层可以蒙骗“刘粉丝”的，所谓“正数”的伪装！

　　刘志斌给原点左侧的负数披上一层所谓“正数”的伪装来掩盖其“对应负数描画对数曲线”的荒谬错误，这好有一比，刘志斌就像那个把自己耳朵掩住，心里想，这下谁也听不见就好像谁也不知道法则为‘y是x的对数’的曲线不可进入Ⅱ、Ⅲ象限的常识了，所以大着胆子大模大样旁若无人地盗铃的蠢贼一样！

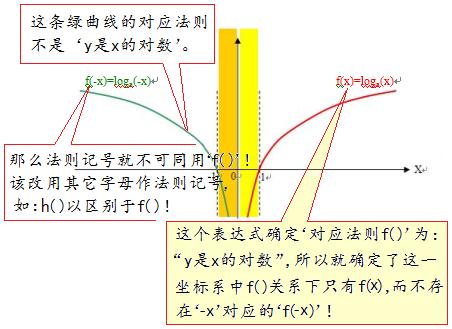
　　刘志斌在他的对数曲线图中，y轴右侧曲线上标注的“f(x)=logax” 就已经确定了函数对应法则“f( )”代表的是“因变量y是自变量x的对数”。这就注定了不允许再给y轴左侧曲线标注相同的对应法则“f( )” 啦!

　　 刘志斌胆大妄为，在y轴右侧已有f(x)=logax的前提下，竟敢指鹿为马地给y轴左侧的曲线标注“f(-x)=loga(-x)”与正统的数学理论相抵触! 
 

　　正确的做法应该是：用另一个字母来作y轴左侧曲线的“函数对应法则”的记号，如“h( )” 以示区别于右侧曲线的“f( )”！因为它们本来就是两个不同“对应法则”的函数！

 
　　f(x)=logax，函数的对应法则为：“因变量y是自变量x的对数”，定义域为x＞0 .

　　h(x)=loga(-x)，函数的对应法则为：“因变量y是自变量x相反数的对数”，定义域为x＜0 .

　　~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
　　

　　其实，这个h(x)已经不是自变量x的对数了，它只是一个“中间变量”的对数！要把这个问题弄清楚，就应该温习一下“复合函数”的概念：

　　如果y是u的函数：y=g(u). 而u又是x的函数：u=ρ(x)　且ρ(x)的值域使g(u)有定义，那么，y通过u的联系也是x的函数：y=h(x) . 我们就称y=h(x)是由函数g(u)及ρ(x)复合而成的函数，简称复合函数.记作y=g[ρ(x)]，其中的u 叫做“中间变量”.

　　~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　现在有：y=g(u)=logau，函数的对应法则为：“因变量y是自变量u的对数”，定义域为u＞0 .

　　而函数u=ρ(x)=-x , 函数的对应法则为：“因变量u是自变量x的相反数”,定义域限定为x＜0 .

　　由函数g(u)及ρ(x) 复合而成的函数h(x)=g[ρ(x)]=loga(-x)同样也不存在“h(-x)”！因为,自变量在定义域(x＜0)上也不可能有互为相反的数值！也就无从谈起“h(-x)”！

　　中学里所讲的函数是“一元实函数”，是两个实变量之间的一种对应关系！我们可以用两个不同的字母来表示这两个变量。譬如我们通常用字母x来表示自变量，用字母y来表示因变量。

　　研究两个变量y和x间的函数关系时，语句“y是x的函数”通常可以用符号 

y=f(x) 或者 y=F(x) 、y=g(x)、y=G(x) 等等简单地表示。这里括弧中的字母x表示自变量，符号“f( )”表示把y和x这两个变量联系起来的对应关系。

　　请注意：这个符号“y=f(x)”仅只表示两个变量之间有某种对应关系，并不明确的表示这种对应关系具体是什么样的法则！明确的法则靠函数解析式（或图象，亦或表格）来表达！

　　举例来说，要表达“y是x的对数函数”，仅只用“y=f(x)=logax”就足够了！

难道刘志斌还以为表示一个自变量名用一个字母x还不够吗？！还需要给自变量名“x”的前面再添个负号“-”才能完整的表达“y是x的对数函数”这一关系吗？！

　　譬如,当自变量取值为8 时，f(8)=log28=3 . 这就足以表达“以2为底，8的对数等于3”！

　　难道刘志斌还以为这样表达“以2为底，8的对数等于3”还不够，还需要再糊弄一个“f(-(-8))=log2(-(-8))=3”才算是完整表达了“以2为底，8的对数是3”这一关系吗？！这是多么可笑的“多此一举”！多么可笑的刘志斌理论！！

　　符号“f(-x)”本来是用来表示函数的自变量在其定义域内存在“互为相反数x和 -x”的前提下，自变量取值为“-x”时所对应的“函数值”,即函数值f(-x)。

　　众所周知，对数函数的定义域是{x│x∈(0，+∞)} ，在这个定义域内，当然绝不可能存在与自变量的某一个取值“x”成相反数的另一个取值“-x”!　这又哪来什么对应于“-x”的对数“函数值f(-x)”呢?！ 

　　老王把题目核心部分那个不等式“(f(x)-f(-f))/x＜0”中的符号“f(x)”和符号“f(-x)”解释为同一个函数f(x)的自变量在定义域中分别取互为相反的数的值“x”和“-x”时，其“-x”所对应的“函数值”，遭到刘志斌的恶意诋毁。所以，老王才引用正统教科书上关于符号“f(x)”和符号“f(-x)”做为“函数的值”的意涵来表达的依据。

　　下面的照片内容就是老王引用的正统教科书上关于“f(x)”和“f(-x)”做为“函数的值”这意涵来表达的例子：

　　请网友们看仔细，这教科书上说，“f(x)是偶函数的标志是：当自变量x取一对互为相反的数的值时，函数的值不变，就是f(-x)=f(x).”我想大多数网友能够看明白：这段话的第一个“f(x)”意为“函数”，而 后面的语句“函数的值不变，就是f(-x)=f(x).”其等式的左右两边的符号“f(-x)”及“f(x)”的意涵都指“函数的值”即等式中符号“f(-x)”和“f(x)”意为“函数值”！

　　分明是刘志斌在诋毁教科书上关于符号“f(-x)”表示“函数的值”！刘志斌却学猪八戒倒打一耙，居然诬蔑老王有把教科书上的正确的知识歪曲为“错误和谎言”！这刘志斌真是不要脸到了极点！

 　　正统教科书解释“f(-x)”为“函数的值”即当函数y=f(x)的自变量在定义域内取一对互为相反的数的值时，其自变量值“-x”所对应的“函数值f(-x)”! 

　　当函数y=f(x)是偶函数时，函数值f(-x)＝函数值f(x)。即同一个函数在自变量取一对互为相反的数的值时，俩自变量值分别对应的俩函数值相等。也就是说偶函数自身是关于y轴对称的。

　　而刘志斌却是这样曲解“f(-x)”的：“当函数f(x)是偶函数时，一定有函数f(-x)也是偶函数，”即刘志斌曲解f(-x)不是原函数y=f(x)中的函数值，而是另一个函数

y=f(-x)，两个函数以y轴为对称。

　　下面这个图片就是刘志斌曲解“f(-x)”之言论的截屏证据：

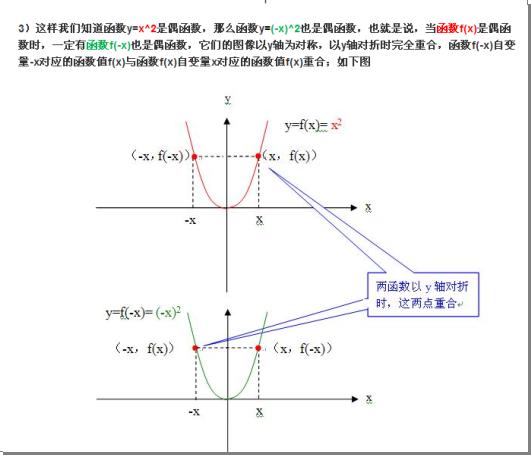
　　刘志斌以函数y=f(x)=x^2为例，荒谬地糊弄出所谓的另一个函数y=f(-x)=(-x)^2 来以示区别于原函数y=f(x)=x^2 ！

　　但凡明白数学的人们都能看出来：刘志斌这所谓的另一个函数y=f(-x)=(-x)^2，与原函数y=f(x)=x^2 根本就是同一个函数！

　　因为俩解析式清楚的表明：第1、它们的定义域相同，都是(-∞，+∞)；第2、它们的值域相同，都是[0，+∞)；第3、它们的对应法则相同，都是“因变量等于自变量的2次方幂”！3个要素都相同，充分证明它们是同一个函数！

　　要表达“因变量等于自变量的2次方幂”仅只用“y=f(x)=x^2”就足够了！

　　难道刘志斌还以为表示一个自变量名用一个字母x还不够吗？！还需要给自变量名“x”的前面再添个负号“-”才能完整的表达“因变量等于自变量的2次方幂”这一函数关系吗？！ 

此题凸显中国基础教育的悲剧，我找一个高中数学老师解答一下，到时回复帖子。

引用 寒湘子 的回复内容：

…… loga(-x)并不意味是负数的对数函数。因为当x本身是负数，上述函数是有意义的。……

1、谢谢 寒湘子，讲了一句公道话！

2、loga(-x)在2、3象限，x是负数，-x就是正数；

3、所以loga(-x)在2、3象限时，还是正数的对数！

4、wanggq不懂，乱喊乱叫随他去吧！

引用 时空——王者之师 的回复内容：

 此题凸显中国基础教育的悲剧，我找一个高中数学老师解答一... 

 谢谢！

引用 wanggq 的回复内容：  　　

连初中学生都知识道，直角平面坐标系中，原点左边的“横坐标”是小于0的数值！在刘志斌的逻辑里，小于0的数值还不是“负数”吗？！

1、  wanggq 真的很差， wanggq 问：“原点左边的“横坐标”是小于0的数值！……小于0的数值还不是“负数”吗？！”

2、loga(-x)在2、3象限，x是负数，-x就是正数；loga(-x)在2、3象限就是正数的对数；

3、小孩子都能看明白的问题， wanggq 看不懂，……

　　1、刘志斌真的很差！他自己明明把f(x)括弧内的x定义为正数，那么正数x的相反数‘-x’当然是负数啦！他刘志斌还半痴半傻的问“-x是负数吗？”！

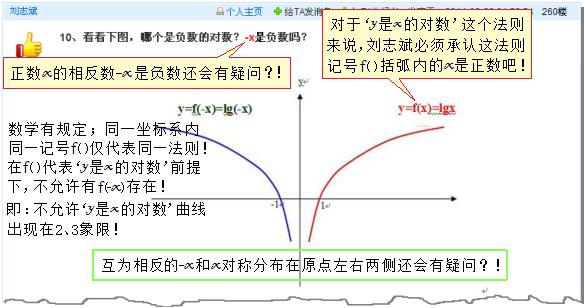
　　2、在同一表达式或同一坐标系内出现的一对“f(x)和f(-x)”，是在同一记号f( )的括号内分别填入互为相反的数值“x和-x”而得到的。

　　当同一记号f( )所表达的具体对应法则为“y是x的对数”时，记号f( )括弧内绝不允许填入互为相反的数值！即绝不允许有刘志斌所谓的“f(-x)”出现！

　　3、当记号f( )的括弧内填入的数值x为正数时，这个‘x’的相反数‘-x’即为负数！连小孩子都能弄明白的道理，活了几十岁的刘志斌居然还弄不懂……！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　针锋相对地反驳刘志斌的276楼

　　1、 寒湘子是被刘志斌的一阵瞎胡搅给搅糊涂啦！寒湘子忽视了同一坐标系中，刘志斌是在给y轴右侧曲线标注了‘f(x)=loga(x)’的前提下又指鹿为马的把y轴左侧曲线标注成“f(-x)=loga(-x)”的！

　　2、同一坐标系中的一对记号“f(x)”和“f(-x)” 表示的是同一个“对应法则f( )”关系下，自变量取一对互为相反的数值‘x’和‘-x’所分别对应的一对函数值。一对互为相反的数值‘x和-x’中的 x是正数时，-x就是负数！ 

　　3、该坐标系里有标注‘f(x)=loga(x)’即确定了“对应法则f( )”代表“y是x的对数”。对于“y是x的对数函数”这一概念来说，‘x’必须是正数！所以，“y是x的对数函数”曲线只可以存在于y轴右侧！绝不允许它又存在于y轴左侧！但是，刘志斌却在同一坐标系里又对y轴左侧的曲线标注同一个代表“y是x的对数 ”之对应法则记号‘f( )’！

　　4、这说明刘志斌弄不懂关于同一坐标系或同一算式中一对函数值记号“f(x)”和“f(-x)” 表示的是同一个“对应法则f( )”关系下，自变量取一对互为相反的数值‘x’和‘-x’所分别对应的一对函数值的这一基础知识！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　曲线上的点的坐标（x，y)，是一个有序“实数对”。平面直角坐标系里，x是横坐标，y是纵标，而且规定了方向：横坐标x轴上原点以右的数值是大于0的，是正数；横坐标x轴上原点以左的数值是小于0的，是负数。

　　坐标平面上y轴右侧的任意一点(x，y)的x坐标值都是正数；坐标平面上y轴左侧的任意一点(x，y)的x坐标值都是负数！

  　　刘志斌真的很差！连初中学生都能明白：“X轴上，原点右侧的任一数值‘x’ 的相反数‘- x’都在原点的左侧”，而刘志斌却不知道！连小孩子都能看明白的道理，刘志斌却看不懂！ 

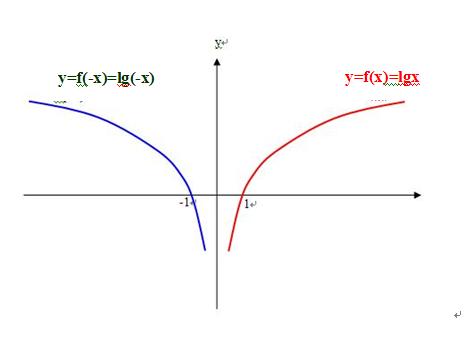
　　在同一个曲线图中讨论函数时，相同的记号“f( )”只表示同一个“函数对应法则”！ 刘志斌既然在y轴右侧的曲线上标注“y=f(x)=lgx”，这个x是正数，而它的相反数“-x” 就是与x对称于原点（居于y轴左侧）的“负数”！对于“负数”是绝不会有“对数”的！即在“y是x的对数函数”这个概念中是不存在“y=f(-x)=lg(-x)”的！刘志斌怎么就胆敢指鹿为马的给y轴左侧的曲线标上“y=f(-x)=lg(-x)”呢？！

　　刘志斌把“y是x的对数函数”胡搅成“y=f(-x)=lg(-x)”是明显错误的！刘志斌这条所谓的“y=f(-x)=lg(-x)”对数曲线上每一个点的横坐标值毫无疑问的都是小于0的数值，居然刘志斌也能把它们都胡搅成“不是负数”！

 　“y是x的对数函数”记作：“y=f(x)=logax” 其定义域是x＞0 即定义域是开区间(0,+∞)，自变量在这个区间上不可能取得互为相反的数值，所以无从谈起f(-x)！

　　即寒湘子指出的：对于x＞0，f(-x)没有定义；对于x＜0，f(x)也是没有定义的 !

　　在同一个曲线图中，刘志斌先给y轴右侧曲线标注“y=f(x)=lgx”表达“y是以10为底，x的对数函数”，再给y轴左侧的曲线标注“y=f(-x)=lg(-x)” ，这就是刘志斌犯的一个错误！

　　刘志斌，你记住：表达“y是以10为底，x的对数”的函数曲线不可能是既在y轴的右侧又在y轴的左侧 ！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　其实，刘志斌那条画在y轴左侧的曲线的对应法则已经不符合“y是以10为底，x的对数”啦！

　　要想得到关于y轴对称的“对数曲线”，只能选‘复合函数’！其对应法则是：“y是中间变量u的对数”, 并非表达y是自变量x的对数！

　　请参阅下述组图：

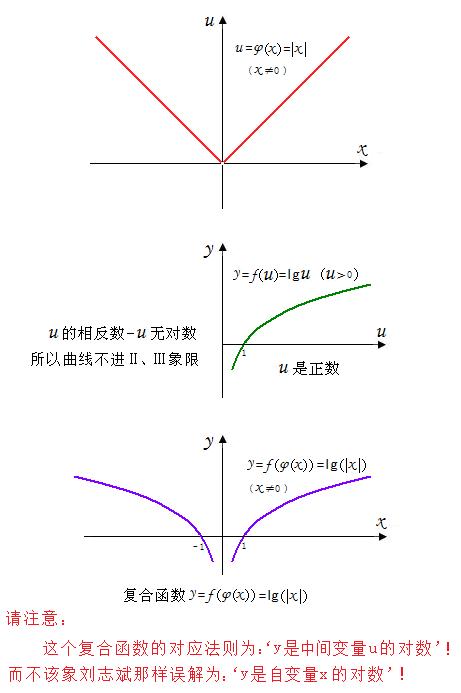
　　y是u的函数：y=f(u)=lg u   (u＞0)，而u 又是x的函数：u=φ(x)=│x│  (x≠0)　

且φ(x)的值域使f(u)有定义，那么，y通过u的联系也是x的函数：y=h(x) . 我们就称

y=h(x)是由函数f(u)及φ(x)复合而成的函数，简称复合函数.记作y=f[φ(x)]，其中的u（ 即φ(x) ）叫做“中间变量”。

引用 wanggq 的回复内容：  　　

……当初留下截屏图片，就是为了防范刘志斌赖账不承认自己的荒谬错误，这证据在此，看刘志斌怎么赖！！

1、这个是 wanggq 自己搞错了，loga(-x)在2、3象限，x是负数，-x就是正数；loga(-x)在2、3象限就是正数的对数；

2、其实提示过很多次了，wanggq 有点儿……