昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
看看这是我们的大师：
1、讨论奇偶性、偶函数时，有一个判断的条件，若f(x)=f(-x)，则函数f(x)为偶函数； 若f(x)=-f(-x)，则函数f(x)为奇函数；
2、当一个函数f(x)是偶函数时，一定有另外一个函数偶f(-x)，f(x)和f(-x)的图像以y轴为对称，完全重合；
3、当一个函数f(x)是奇函数时，一定有另外一个奇函数-f(-x)，f(x)和-f(-x)的图像以原点为对称，完全重合；
各位看看，我污蔑刘老师没？
函数的奇偶性，如同增减性一样，是针对一个函数而言！根本就不存在另一个偶函数f(-x)和另一个奇函数-f(-x).f(-x)是自变量为-x时，f(x)的函数值。我们只讨论f(x)的奇偶性，什么时候有两个函数了。如果像刘老师所讲，f(x)=loga(x),既可以是奇函数也可以是偶函数，只要找到另一个函数f(-x)=loga(-x)，和-f(x)=-loga(-x),就行了，刘老师不是这么教导我们的吗？你看他的图画的有多漂亮，他的思想就有多贫乏和荒唐！
把上面截屏证据中的相关细节放大一点、清楚一点：
上面两行文字可以看得清楚吧!
刘志斌的原文：
-1＜x＜0 f(x)-f(-x)) /x = -f(-x)/x ＜0 如图中绿色部分；
0＜x＜1 f(x)-f(-x)) /x = f(x)/x ＜0 如图中黄色部分；
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
原题目中的不等式“(f(x)-f(-x)) /x ＜0”左边分式的分子是一个“代数和”的运算式！本来是“代数运算”，可刘志斌却将其胡搅为“集合‘并’运算”！多么荒谬的刘志斌胡搅！
引用 寒湘子 的回复内容：
你也知道不对了，那为什么将2换成x或-x,就行了呢？是不是有点那个了，你懂的。
1、 承认“loga(2)-loga(-2）应该等于loga(2)，”这句话是寒湘子当面造谣撒谎了！
2、loga(-x)的定义域是x＜0，将x=2带入得loga(-2）是非法的，是寒湘子自己违背函数基本概念犯了错！
3、loga(x)的定义域是x＞0，loga(-x)的定义域是x＜0，任何情况下都不能把非定义域的数字带入函数解析式！
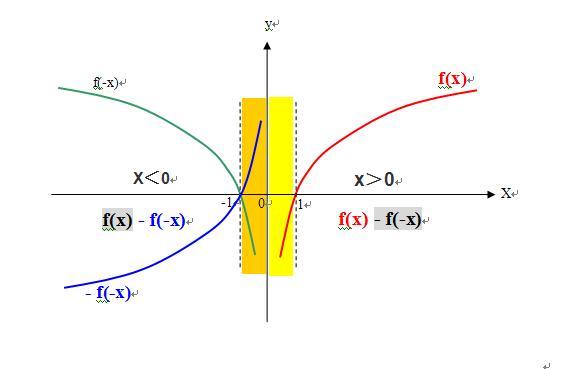
4、如下图，在非定义域上的函数不存在，
1）x＞0 区间上有函数 f(x)，没有函数f(-x)，所以f(x)-f(-x)=f(x)
2）x＜0 区间上有函数-f(-x)，没有函数f( x)，所以f(x)-f(-x)=-f(-x)；
有必要将我对本题的真实看法，重述如下：
我们先看原题：f(x)在0到正无穷大是增函数，f（1）=0，求（f(x)-f(-x)）/x<0时x的范围
解：x无非三种情况：x=0,x>0,x<0
当x=0,若(f(x)-f(-x))/x<0,
则有(f(0)-f(0))/0<0即0/0<0！但是因为0/0无意义，和0的关系不能确定，所以x=0必不是不等式的解集！
当x>0,(f(x)-f(-x))/x<0的解集是{x>0且(f(x)-f(-x))/x<0}可推得{x>0且(f(x)-f(-x))<0}故{x>0且f(x)<f(-x)}......式（1）；
当x<0,(f(x)-f(-x))/x<0的解集是{x<0且(f(x)-f(-x))/x<0}可推得{x<0且(f(x)-f(-x))>0}故{x<0且f(x)>f(-x）}......式（2）；
式(1)、式（2）就是题目的形式上的解集。下面我们证明：
命题一：式（1）和式（2）不是由题目的条件求得。
证明：在式（1）和式（2）的推到过程我们即没有用到“f(x)在0到正无穷上是增函数”的条件，也没有用到f(1)=0的条件，因而式（1）、式（2）的解集不是由题目条件求出。证毕！
命题二：由题目的已知条件，不能求出式（1）和式（2）的解集。
证明：首先，由题目条件，不能得到式（1）的解集{x>0且f(x)<f(-x)}。
x>0,必有-x<0，但是题目条件只可以确定当0<x1<x2时f(x1)<f(x2)，但是对于自变量一个是正一个是负的情况没有给出比较规则，所以得不出f(x)<f(-x)结论。即不能得到式（1）。
同样，由题目条件，不能得到式（2）的解集{x<0且f(x)>f(-x)}。
x<0,必有-x>0，但是题目条件只可以确定当0<x1<x2时f(x1)<f(x2)，但是对于自变量一个是正一个是负的情况没有给出比较规则，所以得不出f(x)>f(-x)结论。即不能得到式（2）。
把上面截屏证据中的相关细节放大一点、清楚一点：
上面两行文字可以看得清楚吧!
刘志斌的原文：
-1＜x＜0 f(x)-f(-x)) /x = -f(-x)/x ＜0 如图中绿色部分；
0＜x＜1 f(x)-f(-x)) /x = f(x)/x ＜0 如图中黄色部分；
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
原题目中的不等式“(f(x)-f(-x)) /x ＜0”左边分式的分子是一个“代数和”的运算式！本来是“代数运算”，可刘志斌却将其胡搅为“集合‘并’运算”！多么荒谬的刘志斌胡搅！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
