昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
10、如果已知函数y=f(x)，通过图像变换得y=af(bx+c)+d，那么变换后的y同样是变换后的x的同类函数，保持原函数的映射关系f( )不变；
我们举一个例子y=1/n,n是正整数，其对应关系如下：
定义域{1,2,3,4,5，...}
值域是{1,1/2,1/3,1/4,1/5,...}对应法则：f(n)=1/n
假如我们将值域的第一个元素去掉变为{1/2,1/3,1/4,1/5,1/6,...}依旧和定义域按顺序一一对应建立映射，这个对应法则变为f(n)=1/(n+1),显然原函数的映射关系f(n)=1/n,变为现映射关系f(n)=1/(n+1).显然映射关系已经改变！
因而刘老师的论断就不对了！
引用 寒湘子 的回复内容：
……
我们举一个例子y=1/n,n是正整数，其对应关系如下：
定义域{1,2,3,4,5，...}
值域是{1,1/2,1/3,1/4,1/5,...}对应法则：f(n)=1/n
假如我们将值域的第一个元素去掉变为{1/2,1/3,1/4,1/5,1/6,...}依旧和定义域按顺序一一对应建立映射，这个对应法则变为f(n)=1/(n+1),显然原函数的映射关系f(n)=1/n,变为现映射关系f(n)=1/(n+1).显然映射关系已经改变！
1、函数y=1/(n)和函数y=1/(n+1)，是同类函数，因为它们的映射关系都是1/( )；
2、说明函数y=(x)^-1和函数y=(x+1)^-1都是幂函数，映射关系是( )^-1；
3、我们可以画出图像，他们的图像相同，都是反比函数的双曲线；
4、“显然原函数的映射关系f(n)=1/n,变为现映射关系f(n)=1/(n+1).显然映射关系已经改变！”寒湘子为什么要睁着眼说瞎话？
5、应该说1/n≠1/(n+1)，但是映射关系都是1/( )，是指数为-1次的幂函数！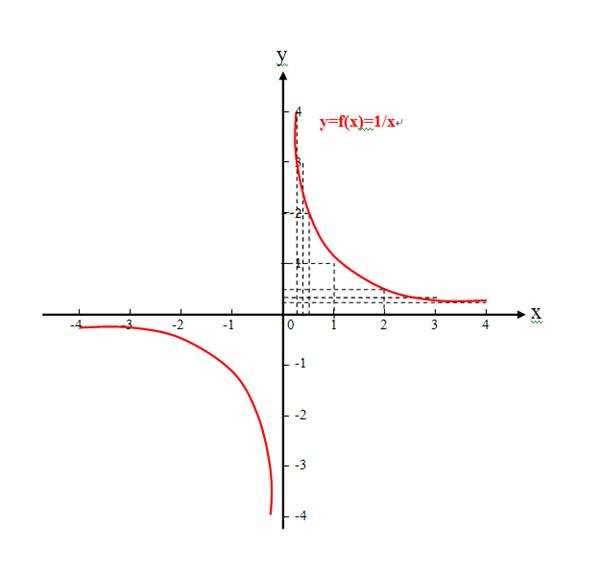
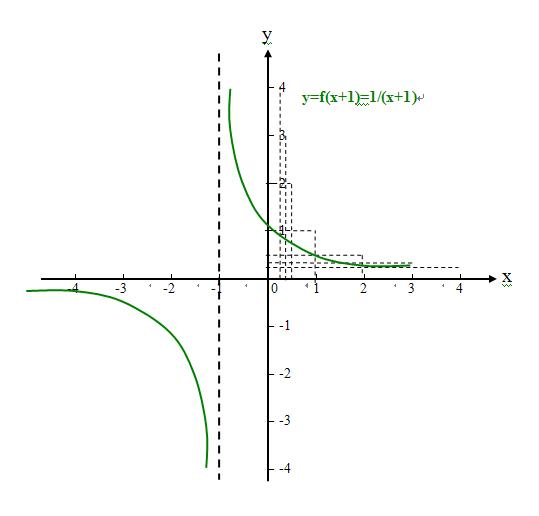
实际映射关系已经变了，既然不承认，很容易的。
假设一个集合X={1,2,3,4}到集合Y={1,4,9,16}按y=x^2构成一一映射。这个映射按你的讲法是（）^2.假设中间增加到集合X'={x1',x2',x3',x4'},映射关系是x'=sinx,于是X'={sin1,sin2,sin3,sin4}.X'到Y'的映射任然是y=()^2.显然Y={(sin1)^2,(sin2)^2,(sin3)^2,(sin4)^2}，我的问题是从X到Y的映射，在于刘老师看来，是()^2还是sin()?幂函数和正弦函数是否，映射关系不变？
刘老师在40楼和我争论时，曾经断言：
1、楼主 的问题给出的条件：
1）f(x)在0到正无穷大；
2）增函数；
3）f（1）=0；
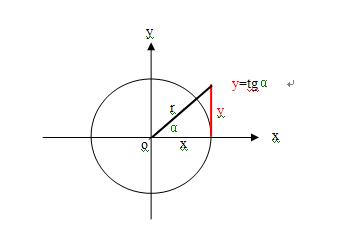
2、符合三条件的函数f(x)，只有对数函数 logaX a＞1，如图；
而在552楼批驳老王是又是如下讲：
引用 wanggq 的回复内容：
最初，刘志斌是一口咬定说：“符合f(x)在0到正无穷大是增函数，f(1)=0,这种条件的只有对数函数”还用非常刻薄的言语与对手<烟雨朦朦>激烈的争辩了很多时候，经过争辩也从对手<烟雨朦朦>的发言中学到了“符合题目条件的函数多得很”的知识，于是刘志斌也把原来理直气壮的咬定“唯一只有对数”的口气缓和为“可以理解为对数”！
1、这也是造谣！
2、基本初等函数图像中，符合“f(x)在0到正无穷大是增函数，f(1)=0，”这三个条件的只有对数函数”；
3、其它符合f(x)在0到正无穷大是增函数，f(1)=0,这三条件的函数有很多，但都不是基本初等函数定义式的图像；
4、wanggq 能举出第二个符合f(x)在0到正无穷大是增函数，f(1)=0,这三条件的基本初等函数定义式的图像吗？
请问40楼有讲“基本的初等函数”吗？为什么那时不讲，而要老王指出其错误时要加上“基本的初等函数”呢？
那么什么是“基本的初等函数”呢？刘老师认为y=f(x)=exp(x),是基本的初等函数是没有问题吧？根据刘老师大量论述图形经过平移、旋转、甚至拉伸，映射关系或函数变换是不变的，如y=sin(x)和y=sin(x-1）都是一样的映射或函数，因为形式一样y=sin(),是吧？你多次教导，希望我不至于理解错。好了，我们将这个函数图象向下平移e个单位，这个函数应该还保持一样的函数关系或映射（根据刘老师的理论），现在函数变为y=exp(x)-e按刘老师的概念也应该可以记为：y=exp()，按刘老师逻辑显然应该属于“基本的初等函数”
现在y=exp(x)-e，在0到正无限大区间上显然是增函数，并且f(1)=0.按刘老师逻辑也是相符的，怎么冤枉老王造谣呢！
实际原题根本没有说这个函数是“基本的初等函数”，刘老师算不算无中生有呢！
引用 寒湘子 的回复内容：
实际映射关系已经变了，既然不承认，很容易的。……
1、已知函数y=f(x)，这个函数属于f( ) 类函数；
2、通过图像变换得函数y=af(bx+c)+d，该函数是否还属于f( )类函数？
3、函数y=af(bx+c)+d可变形得：(y-d)/a=f(bx+c)，令y'=(y-d)/a，x'=bx+c，则有函数
y‘=f(x’)
很明显y‘=f(x’)是属于f( )类函数；
4、那么y'=(y-d)/a也是个y到y'的一次函数，存在y到y'的一次幂函数的映射关系；
5、那么x'=bx+c也是个x到x'的一次函数，存在x到x'的一次幂函数的映射关系；
6、那么4、5的映射关系，并没有改变函数f( )的映射关系，属于f( )类函数的图像没有改变；
7、在处理实际问题时，我们恰恰是利用了这一点，常常将形式复杂的函数y=af(bx+c)+d，化简为y‘=f(x’)的形式，使问题简化，使问题的变量间的函数关系更简明！
引用 刘志斌 的回复内容： 引用 寒湘子 的回复内容： 实际映射关系已经变了，既然...
其荒谬我在667楼已有论述:
刘老师讲：“函数图像变换”，函数的类别并没有变化。是对数函数，图像变换后还是对数函数；是幂函数，图像变换后，还是幂函数；是正弦函数，图像变换后还是正弦函数，……。
我们来看看上述话有几句是对的：
1、“函数图像变换”，函数的类别并没有变化
y=kx+b，一次函数；令x=(u-b)/k,y=u，改写自变量为x，y=x，幂函数（也是一次函数）
令x=(sinu-b)/k，y=sinu，改写自变量为x，y=sinx正弦函数
令x=(cosu-b)/k，y=cosu，改写自变量为x，y=cosx正弦函数
令x=(exp(u)-b)/k，y=exp(u)，改写自变量为x，y=exp(x)指数函数
令x=(u^a-b)/k，y=u^a，改写自变量为x，y=x^a幂函数
令x=(lnu-b)/k，y=lnu，改写自变量为x，y=lnx对数函数
还可以变为反正切函数等等。只要愿意可以变成任何类型函数。只要你说这是一类函数。何为，函数类别没有变化。
8、我们总结一下：
1）函数y=-3loga(-4x-6)+5，可变形得：(y-5)/(-3)=loga(-4x-6)，令y'=(y-5)/(-3)，x'=(-4x-6)，则有函数
y'=loga(x')
则，y‘是x’的对数函数；y也是x的对数函数。
2）函数y=Asin(ωx+φ)+B，可变形得：(y-B)/A=sin(ωx+φ)，令y'=(y-B)/A，x'=(ωx+φ)，则有函数
y'=sin(x')
则，y‘是x’的正弦函数；y也是x的正弦函数。
3）函数y=d(bx+c)^a+e，可变形得：(y-e)/d=(bx+c)^a，令y'=(y-e)/d，x'=bx+c，则有函数
y‘=(x’)^a
很明显y‘是x’的幂函数；y也是x的幂函数。
引用 寒湘子 的回复内容：
……请问40楼有讲“基本的初等函数”吗？为什么那时不讲，而要老王指出其错误时要加上“基本的初等函数”呢？
1、我在2楼发言的帖子里，就已经说过了：看看2楼的发言如下：
1、这个题目是在哪一个章节出现的题目？如果是在基本初等函数的内容，也可以这样理解：
1）因为f（1）=0，且在0到正无穷大是增函数，所以这个函数可以理解为f(x)=logaX，a＞1；
2）那么函数f(-x)=loga(-X)，a＞1，定义域为0到负无穷大是减函数；
3）这样f(x)-f(-x)是一个分段函数：
当x＞0时，f(x)-f(-x)=f(x)，这样，在区间（0，1）上，（f(x)-f(-x)）/x<0；
当x＜0时，f(x)-f(-x)= - f(-x)，这样，在区间（-1，0）上，（f(x)-f(-x)）/x<0；
2、寒湘子50楼等说过好多次了，我解释好多次了，寒湘子早就明白，寒湘子还是要睁着眼说瞎话，为了什么？
引用 寒湘子 的回复内容： 刘老师直到爬到81楼才明白，还有不是对数函数的可能，但...
1、对不熟悉基本初等函数图像的寒湘子 ，寻找附和题意的函数，是一种思路；
2、那么寒湘子认为“附和题意”的函数，寒湘子不是设想出好多吗？
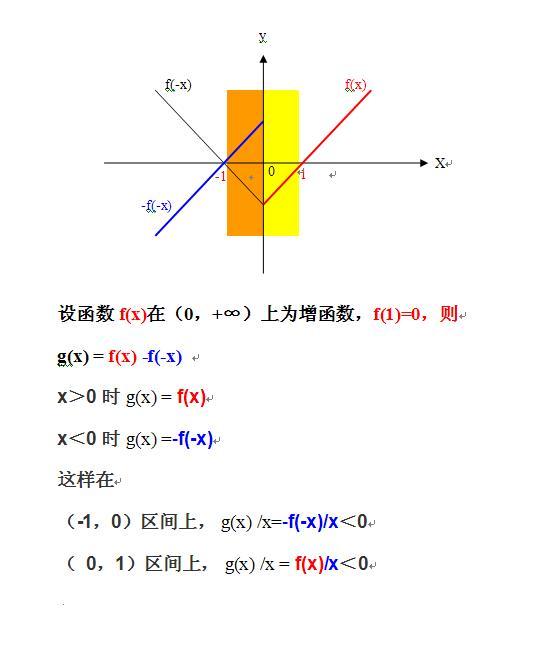
3、离开初等基本初等函数，其实不需要考虑具体是什么函数，可以设定在0到无穷大、增函数、过f(1)=0点的任-函数f(x)就可以了，所以有以下图；
4、并非一定是直线，可以是上凹的曲线，也可以是下凹的曲线，只要在1、4象限、增函数、过f(1)=0点就符合题意；不影响题解的正确答案，题解的答案是唯一的，即
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
