昨天一道高中的数学题，我竟然不会做了 点击：22038 | 回复：1402
楼主最近还看过
我们先看原题：f(x)在0到正无穷大是增函数，f（1）=0，求（f(x)-f(-x)）/x<0时x的范围
解：x无非三种情况：x=0,x>0,x<0
当x=0,若(f(x)-f(-x))/x<0,
则有(f(0)-f(0))/0<0即0/0<0！但是因为0/0无意义，和0的关系不能确定，所以x=0必不是不等式的解集！
当x>0,(f(x)-f(-x))/x<0的解集是{x>0且(f(x)-f(-x))/x<0}可推得{x>0且(f(x)-f(-x))<0}故{x>0且f(x)<f(-x)}......式（1）；
当x<0,(f(x)-f(-x))/x<0的解集是{x<0且(f(x)-f(-x))/x<0}可推得{x<0且(f(x)-f(-x))>0}故{x<0且f(x)>f(-x）}......式（2）；
式(1)、式（2）就是题目的形式上的解集。下面我们证明：
命题一：式（1）和式（2）不是由题目的条件求得。
证明：在式（1）和式（2）的推到过程我们即没有用到“f(x)在0到正无穷上是增函数”的条件，也没有用到f(1)=0的条件，因而式（1）、式（2）的解集不是由题目条件求出。证毕！
命题二：由题目的已知条件，不能求出式（1）和式（2）的解集。
证明：首先，由题目条件，不能得到式（1）的解集{x>0且f(x)<f(-x)}。
x>0,必有-x<0，但是题目条件只可以确定当0<x1<x2时f(x1)<f(x2)，但是对于自变量一个是正一个是负的情况没有给出比较规则，所以得不出f(x)<f(-x)结论。即不能得到式（1）。
同样，由题目条件，不能得到式（2）的解集{x<0且f(x)>f(-x)}。
x<0,必有-x>0，但是题目条件只可以确定当0<x1<x2时f(x1)<f(x2)，但是对于自变量一个是正一个是负的情况没有给出比较规则，所以得不出f(x)>f(-x)结论。即不能得到式（2）。
5）函数定义域的求法：做几道题，大家就知道是怎么回事
Ⅰ、抽象函数定义域的求法，常见题型有三种：
一，已知f(x）的定义域，求f(g(x））的定义域.
例1，已知f(x）的定义域为（-1，1），求f(2x-1）的定义域.
略解：由 -1<2x-1<1有 0<x<1
∴f(2x-1）的定义域为（0，1)
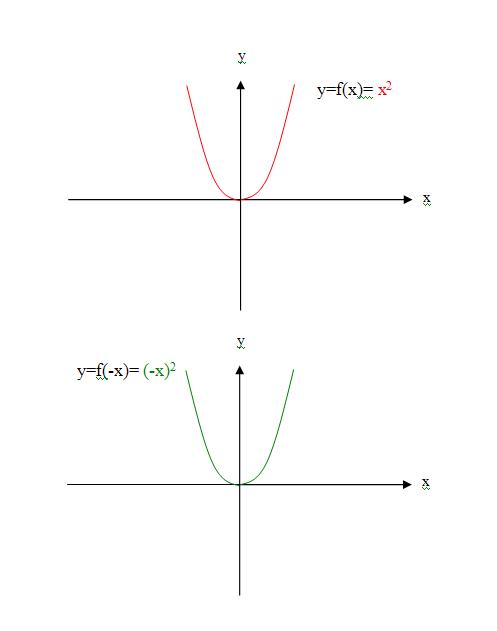
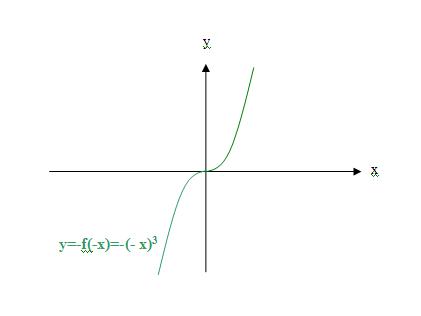
例，已知函数f(x)在0到正的无穷大，求函数f(-x)、-f(-x)的定义域
略解：-x＞0，x＜0。
∴f(-x)、-f(-x)的定义域为0到负无穷大，即x＜0。
二，已知f(g(x))的定义域，求f(x)的定义域.
例2，已知f(2x-1)的定义域为(0，1)，求f(x)的定义域。
解：已知0<x<1，设t=2x-1
∴x=(t+1)/2
∴0<(t+1)/2<1
∴-1<t<1
∴f(x)的定义域为(-1,1)
注意比较例1与例2，加深理解定义域为x的取值范围的含义。
三，已知f(g(x))的定义域，求f(h(x))的定义域.
例3，已知f(2x-1)的定义域为(0，1)，求f(x-1)的定义域。
略解：如例2，先求出f(x）的定义域为(-1，1)，然后如例1
有 -1<x-1<1，即0<x<2
∴f(x-1)的定义域为(0，2)
Ⅱ、求能使函数有意义的一切实数所组成的集合。
其主要根据：
①分式的分母不能为零
②偶次方根的被开方数不小于零
③对数函数的真数必须大于零
④指数函数和对数函数的底数必须大于零且不等于1
例4，已知f(x)=1/x+√（x+1），求f(x）的定义域。
略解：x≠0且x+1≧0，
∴f(x）的定义域为[-1，0）∪（0，+∞）
注意：答案一般用区间表示。
例5，已知f(x)=lg（-x^2+x+2），求f(x）的定义域。
略解：由-x^2+x+2 >0 有 x^ 2-x-2 <0
即-1<x<2
∴f(x）的定义域为（-1，2)
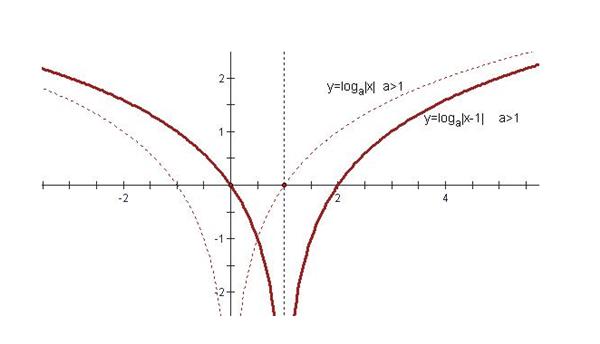
例，已知函数f(x)=lg(x)，定义域为x＞0，求函数f(-x)=lg(-x)的定义域。
略解：-x＞0，x＜0。
∴函数f(-x)=lg(-x)的定义域是x＜0；
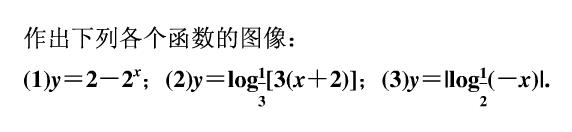
Ⅲ、函数应用题的函数的定义域要根据实际情况求解。
例6，某工厂统计资料显示，产品次品率p与日产量x（件）（x∈N,1≦x<99）的关系符合如下规律：
x 1 2 3 4 … 89
p 2/99 1/49 2/97 1/48 … 2/11
又知每生产一件正品盈利100元，每生产一件次品损失100元.
求该厂日盈利额T（元）关于日产量x（件）的函数；
解：由题意：当日产量为x件时，次品率p=2/(100-x)
则次品个数为：2x/(100-x），正品个数为：x-2x/(100-x）所以T=100[x-2x/(100-x) ]-100·2x/(100-x)
即T=100[x-4x/(100-x) ],(x∈N且1≦x≦89)
大家现在已经明白，刘老师的言论多么离谱，什么连对数都不懂，什么没有资格说题目是错的，什么撒谎或谎言！就连最后求起定义域还求出一个什么解集是{xIx不等于0}，这个集合是什么东西，有这样写的吗？
大家容忍他，不和他计较，也给了他很多机会，这次我必须较真。他不是说我从1楼到800多楼都是在撒谎吗？好！我们就看一看刘老师坚持的是什么真理！
他为“矢量控制”是谎言而辩论，他为证明“异步电动机转矩滑差特性是幂函数”而辩论，他为一个本来就错的题目而大放厥词，他认为函数的定义域到值域的映射是一一映射，他认为loga(2)-loga(-2）应该等于loga(2)，他甚至在讨论奇偶性时也在谈两个函数。试问，哪一条他是对的。
除了污蔑对手，将对手说成是骗子或说谎者，目的不就是为了证明，他没有错吗？死不认错，我原谅你，但是你贬低对手的行为，我不会给你任何机会。
我好言相劝，算了见好就收，留点颜面。但是刘老师认为他很行，一定要将对手辩倒。而且越来越离谱，瞧不起这个看不起那个，说我没有资格说题目出错！你当你是谁？
还叫我说你什么呢！
老王把不等式“(f(x)-f(-x))/x＜0”中的符号“f(x)”及“f(-x)”解释为函数的自变量取一对互为相反数时分别对应的俩函数值，遭到刘志斌的恶毒诋毁。
所以，老王就引用高校教科书上的相关内容的照片资料来证明老王的解释是有根有据的。
下面的截屏图片就是老王的原贴内容：
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
刘志斌撒谎、当面造谣！恶意的将老王本来是用正统理论来作我们解题的正确“依据”的事实，诬蔑成：“堂而皇之的把它歪曲成‘错误和谎言’”！
这是截屏证据，证明刘志斌撒谎、当面造谣！恶意诬蔑对手：
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
