昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
对于函数f(x)=3x ，有f(-x)=-3x ，即f(-x)= - f(x)；
而对于函数f(x)=x^2 ，有f(-x)= (-x)^2=x^2，即f(-x)=f(x).
一般地，对于函数f(x)：
2．如果对于函数定义域内任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。
3.对于函数定义域内任意一个x，若有f(-x)≠ - f(x)，且f(-x)≠f(x)，那么函数f(x)既不是奇函数，也不是偶函数！此种情况我们就说函数f(x)不具有奇偶性。
4.如果函数定义域内任意一个x，其相反数“-x”不在该定义域内，那么，函数f(x)的曲线就必然不经过-x处，因为函数f(x)在-x处已经没有定义了！坐标平面内根本就不存在( -x ，f(-x))这种点 ！当然就既不会有 f(-x) = -f(x)，也不会有 f(-x) = f(x)。所以，函数f(x)也当然的既不是奇函数，也不是偶函数！此种情况当然是函数不具有奇偶性的情况！
（注：对于4. 坐标平面内不存在(-x，f(-x)这种点，是因为函数f(x)在-x处没有定义，即以f(x)的映射法则来说没有对应于-x的y值。而坐标平面内确实存在(-x，f(x))这种点与函数f(x)在定义域内的点(x，f(x))关于y轴对称，但是，点(-x，f(x)却不是函数f(x)上的点！）
函数f(x)如果用图象来表示，那么函数是否“具有奇偶性”就是一目了然的啦！
下面是函数f(x)=0.5x+2 的图象：
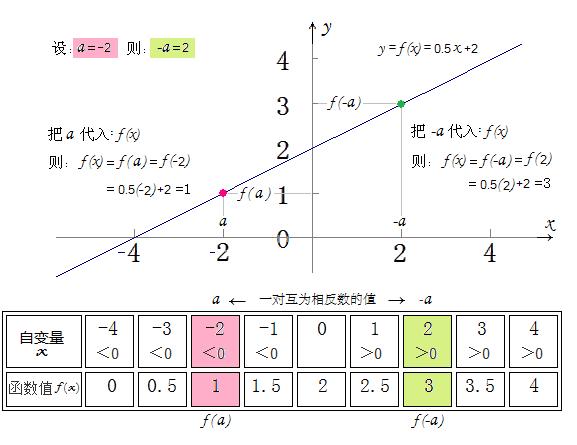
因为函数f(x)=0.5x+2 的映射法则是明确的，所以我们根本不需象刘志斌那样“解方程”或“解不等式”，一眼就看到该函数f(x)的定义域是{x│x∈R} 即一切实数。
假设我们用字母a代表函数f(x)定义域内任意一个数，则对应的相反数就是
“-a”.
如果 a = -2，则，-a = 2 .
把这两个互为相反的数分别代入函数f(x)＝0.5x+2，就分别得到：
“函数值f(a)”及“函数值f(-a)”
f(a) =0.5(-2)+2=1 ； f(-a) =0.5(2)+2=3 ．
那么，(f(a)-f(-a)) /a ＝(f(-2)-f(2))/(-2)＝(1-3)/(-2)=1
大家都知道，这是“代数运算式”！刘志斌（伪“大师”）却不认得这是“代数运算式”！
从图象上，我们一眼就看到函数f(x)=0.5x+2 既不是奇函数，也不是偶函数。所以我们说函数f(x)=0.5x+2 不具有“奇偶性”。
大家都知道，在代数里，可以用字母代表数。而且字母也可以不限于a、b、c、或x、y、z ！
在上例中，我们是用字母a来代表函数f(x)=0.5x+2 定义域内任意一个数值，当然我们也可以用字母x来代表函数f(x)=0.5x+2 定义域内任意一个数值！
下图就是用字母x来代表函数f(x)=0.5x+2 定义域内任意一个数值的情形：
如果 x = -2，则，-x = 2 .
把这两个互为相反的数分别代入函数f(x)＝0.5x+2，就分别得到：
“函数值f(x)”及“函数值f(-x)”
f(x) =0.5(-2)+2=1 ； f(-x) =0.5(2)+2=3 ．
那么，(f(x)-f(-x)) /x ＝(f(-2)-f(2))/(-2)＝(1-3)/(-2)=1
大家都知道，这是“代数运算式”！刘志斌（伪“大师”）却不认得这是“代数运算式”！
从图象上，我们一眼就看到函数f(x)=0.5x+2 既不是奇函数，也不是偶函数。所以我们说函数f(x)=0.5x+2 不具有“奇偶性”。
1、我们仔细看看上述高中数学的一道求函数定义域的题目
1）首先要明确，lg(x-2)+√5-x，是一个“函数”，不是一个“代数式”；/lg(x-2)+√5-x本就是一个代数式，因为有变量"x"，x是表示未知数的字母，况且，函数表达式本身就是“代数式”，但是：刘老师将lg(x-2)+√5-x称为函数就笑话了，因变量呢？因变量都没有出现你讲谁是谁的函数！不懂就不要装懂，你给我翻任何一本书会把“lg(x-2)+√5-x”这个表述称为函数，我就认，只要不是你写的！/
2）首先要明确，lg(x-2)+√5-x，是一个“函数运算”，不是一个“代数运算”；/不是函数谈什么函数运算，刘老师，你能找到一本书讲这叫做函数运算的，只要不是你写的，我还认！/
3）有什么不同吗？不同的是，只要是函数，只要是函数运算，字母x的取值必须在定义域上；/函数的定义域如何确定，不是由代数式的意义确定吗？“字母x的取值必须在定义域上”也真专业，像谈哲学而不是数学，数学不用这种语言！/
引用 wanggq 的回复内容：
原题目中的不等式“(f(x)-f(-x)) /x ＜0”左边分式的分子是一个“代数和”的运算式！本来是“代数运算”，可刘志斌却将其胡搅为“集合‘并’运算”！多么荒谬的刘志斌胡搅！ ... /这本身就是代数式，而不是函数，函数需要指明因变量，这里有x
1、看到了吧，wanggq 把“(f(x)-f(-x)) /x ”函数、函数式、函数的运算，当做是“代数运算”；
2、求函数“(f(x)-f(-x)) /x “的定义域，就是求各个函数f(x)、-f(-x)) 、1/x的定义域的交集；/你昨天不是告诉我要求“并集”吗？今天怎么成了“交集”？应该回去学习的是你，不是别人！/
3、函数“f(x)-f(-x))”的值域，可以理解为分段函数，分段函数的值域，就是各段函数值域的“并集”
4、wanggq处于学习过程中，有各种疑问是可以理解的！
6、下来我们讨论主楼的题目，先看原题：“f(x)在0到正无穷大是增函数，f（1）=0，求（f(x)-f(-x)）/x<0时x的范围。”
1）已知函数f(x)在0到正无穷大，即定义域x＞0 /我说我喜欢吃青菜，我就一定不吃肉吗？题目只讲一个区间上是增函数，难到这个函数就是增函数！要单调干什么？老王早就说你理解定义域错了，还解什么定义域，吃饱了撑得！一个5秒都不要的题目，拿到这里丢人现眼！这可是要有很深的修为，非大师莫属！/
2）求的“（f(x)-f(-x)）/x<0时x的范围”中，（f(x)-f(-x)）/x是个函数式；
3）首先求函数式（f(x)-f(-x)）/x的定义域
4）“函数定义域的意义 ”：
a、函数只有在其定义域上，有意义；/大师就是大师，人家讲定义域是使函数有意义的自变量的集合。大师就要反过来说，这样才不同嘛！要不怎么显得他有学问呢？/
b、函数的运算，必须在其定义域上进行；/函数怎样你运算，不要按代数运算规则吗？一般讲先有代数规则，才能确定函数定义域。比如，负数不能开平方，为什么？因为没有实数可以自乘得到一个负数。同样没有正数的幂可以为0.所以真数就不可能为0.刘老师强调函数运算是和代数运算不同的是本末导致。函数在代数里就是变量。但是如果不指明因变量，就不可以叫函数。另外不是所有代数方程都是表示函数关系！如在坐标原点，半径为r的圆的方程可以表示为x^2+y^2=r^2，这时在初等数学函数的概念下，y不是x的函数！刘老师，很惊讶吧！/
c、函数的定义域是以函数是否有意义为前提，不仅与函数解析式的性质有关，而且和讨论的实际问题有关，不是随意确定的；/可解析式不是可能是代数式吗？不是代数规则决定函数的意义，而是函数意义决定代数规则不是很难以理解吗？/
在一段叙述中，语境不同，符号“f(x)”的意涵也不同！请看这正统教科书上有榜样：
请看教科书上的这段：“f(x)是偶函数的标志是：当自变量x取一对互为相反数的值时，函数的值不变，就是f(-x)=f(x)．”这句话的第1个“f(x)”明显是指“函数”，而后面的等式“f(-x)=f(x)”中所提及的“f(-x)”及“f(x)”都是指同一个函数中的“函数值”！
但凡是明白人，都不可能领会不出来！刘志斌到底是理解能力有问题，领会不到这等式中的“f(-x)”及“f(x)”皆表达“函数的值”！还是明知是指“函数的值”却愣要故意将其胡搅成“两个函数”？如果是后者，那就说明刘志斌恶劣！！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
