符号“f(x)”在不同的语境里，其意涵是不同的：

　　这是另一本数学教科书上给我们的示范：

　　f(x)是偶函数的标志是：当自变量x取一对互为相反的数的值时，函数的值不变，就是f(-x)＝f(x) 。

　　请看1222楼的照片（来自数学教科书）的内容，这句子中第1个“f(x)”很明确是“函数”；这句子最后的，即等式“f(-x)=f(x)”右边的“f(x)”明显的是“函数的值”！当然，等式左边的“f(-x)”同样明显的是“函数的值”！

　　在正统的数学教科书里，从来没有用符号“f(-x)”表示过“函数”！这是因为用符号“y=f(x)”表示“y是x的函数”，已经足以表达因变量y与自变量x之间有映射的关系存在，而且x既可以代表正数，也可以代表负数。哪还用得着多此一举再添个这样的符号“f(-x)” 来表示“x的函数”？！

　　符号“y=f(x)”表示“y是x的函数”，自变量是x，因变量是y.　因变量也叫做自变量的函数。

　　有时图个简便，简洁用符号“f(x)”表示“x的函数”，自变量是x，因变量是f(x)。即这种语境里的“f(x)” 其括弧内的x表示的是一个“量”(自变量)，而不是一个数值；

　　如果换一种语境，使x代表函数定义域内的任意一个数值，则f(x)就代表按照既定的映射法则f( )而得到的对应于x值的“函数值”。

　　例如，函数f(x)=x^3+1  当x＝2时，对应的函数值f(x)=f(2)＝(2)^3+1=9；当x=-2时，对应的函数值f(x)=f(-2)＝(-2)^3+1=-7 .

　　而符号“f(-x)”则纯粹是人们为了研究讨论函数f(x)是否具有对称性或具有哪种对称性，所引用的一个函数值符号！  

　　要研究讨论函数的对称性，我们就得从对称的自变量值入手，什么是对称的自变量值呢？对称的自变量值就是定义域上分处于0点左右两侧，且距0点等距离的横坐标值，即一对互为相反的数的值。  

　　当自变量在定义域内分别取一对互为相反的数（x与-x）的值时，其“-x”所对应的函数值就是f(-x).  

 　　用符号“y=f(x)”表示“y是x的函数”，已经足以表达因变量y与自变量x之间有映射的关系存在，而且x既可以代表正数，也可以代表负数。还用得着象刘志斌那样再添个这样的符号“y=f(-x)” 来表示“y是x的函数”吗？！

　　刘志斌再添个这样的符号“y=f(-x)” 来表示“y是x的函数”纯属多此一举！！

第1、　　　　　　　　　　　

　　当已知函数f(x)是偶函数时，该函数关于y轴的对称曲线是它自身！即该函数定义域中任意一个自变量x与其相反数-x所分别对应的俩函数值是相等的！

即：  f(-x)=f(x)。

　　 这里的等式f(-x)=f(x) 原本是表达：同一个偶函数上，自变量取一对互为相反的数的值时，分别对应的俩函数值相等的意思！可刘志斌却罔顾教科书上的正统理论，偏要执意的将记号“f(-x)”的意涵胡搅成“有别于指定函数f(x)映射法则的另一个函数”！

　　我们引用刘志斌分别描述的f(x)=x^2和f(-x)=(-x)^2这俩图象，通过它们的完全重合来说明这一原理：

　　通过把刘志斌的f(x)=x^2和f(-x)=(-x)^2的俩曲线重叠起来，让我们清楚的看到两条曲线完全重合！

　　这充分说明仅用1个符号“f(x)=x^2”就足以完整的描述y与x之间的这个函数关系：“因变量y是自变量x的2次幂”！完全没有必要象刘志斌那样再添一个“f(-x)=(-x)^2”来重复描述“因变量y是自变量x的2次幂”！添一个“f(-x)=(-x)^2”来重复描述这一函数关系，纯粹是多此一举！ 

第2、　　　　　　　　　　　　　

　　当已知函数f(x)是奇函数时，该函数关于y轴的对称曲线是另一条曲线，即另一个奇函数。即便是另一个函数，也不该用符号“f(-x)”来表它，因为符号“f(-x)”已经被我们赋予了“在同一条曲线上，自变量取定义域上一对儿互为相反的数的值(x和-x)时，其‘-x’所对应的函数值”这一概念！

　　对于这另一个奇函数，单独的情形下，也可以用f(x)表示，因为y和x这两个变量之间的任何对应关系都可以用符号“f( )”来表示！但是，在研究讨论同一个问题的情形下，不同的函数对应关系就应该用不同的符号加以区别！如：F( )与f( )相区别，或者如：g( )与f( )相区别 。 

　　举例来说，奇函数y=x^3可以表示成f(x)=x^3 ；与之相互之间(关于y轴)对称的另一个奇函数 y= -x^3也可以表示成f(x)= -x^3 . 

　　但在研究讨论同一个问题时，就应该用不同的符号加以区分．如：对于奇函数

f(x)=x^3 ，与之相互之间(关于y轴)对称的另一个奇函数则用g(x)=-x^3  加以区分。

　　请注意：但凡是奇函数，与其相互之间(关于y轴)对称的另一个奇函数必然同时也是与其相互之间(关于x轴)对称的!  如：f(x)=x^3 , g(x)=-x^3 ，则g(x)=-x^3=-f(x).

　　所以，与已知奇函数f(x)关于y轴相互对称的另一个奇函数可以表示成“-f(x)”因为符号“f(x)”也是函数的符号嘛，但却不可以表示成“f(-x)”!因为符号“f(-x)”只能是“函数值符号”！

第3、　　　　　　　　　　　　　

　　当已知函数f(x)是奇函数时，若象刘志斌那样用f(-x)表示该函数关于y轴的对称函数，那么，这个刘志斌所谓的函数“f(-x)”既与函数f(x)相互之间关于y轴对称，也与函数f(x)相互之间关于x轴对称！

　　这样刘志斌理论中的矛盾就凸现出来了！

　　函数“f(-x)”与函数f(x)关于y轴对称，则：f(-x)=f(x) ；

　　函数“f(-x)”与函数f(x)关于x轴对称，则：f(-x)=-f(x) ；

　　所以必然推出：f(x)=-f(x) 。

　　很明显，当奇函数y=f(x)不是常函数y=0时， f(x)=-f(x)就是一个矛盾的结果！

　　 f(x)= - f(x) 即同一个自变量值x，按照同一个既定的映射法则f( ) 得出了两个互为相反的“象”！所以，我们看出：刘志斌理论明显的与正统数学理论中关于映射的定义相抵触！

 　　以f(x)=x^3为例来说，在正统理论里，当x≠0时，x^3≠ -x^3  ，但在刘志斌理论里，任意x都有： x^3＝－x^3 ？！很明显，刘志斌理论是荒谬的！

　　下图中的俩坐标系上分别有红色曲线y=f(x)=x^3 及绿色曲线y=-x^3 即刘志斌所谓的y=f(-x)=(-x)^3，是摘自刘志斌跟帖中的曲线，我们把刘志斌的这俩曲线重叠在同一个坐标系里，可以从中看到矛盾的结论：“f(x)= - f(x)”　

　　因为刘志斌的“函数y=f(-x)”与y=f(x)相互之间是关于y轴对称的，所以，刘志斌的 f(-x)与f(x)是相等的，即：f(-x)=f(x) ；同时，刘志斌的“函数y=f(-x)”与y=f(x)相互之间又是关于x轴对称的，所以他刘志斌的f(-x)与f(x)又是相反的！即：f(-x)=-f(x) .

　　请注意，∵f(-x)=f(x) 、同时f(-x)=-f(x) ，∴必然推出矛盾的：f(x)=-f(x) ！大家看，这奇函数y=x^3  ,自变量取任何一个非零的x值，对应的函数值f(x)绝不可能等于它的相反数“-f(x)” ！

　　举例来说：若x=2，则，f(x)=f(2)=(2)^3=8  那么，-f(x)=-f(2)=-(2)^3=-8 。大家都知道，函数值“f(2)=8”绝不可能等于它的相反数“-f(2)=-8” ！

　　正统教科书上把f(x)与f(-x)这一对儿符号定义为同一函数的自变量取定义域上一对互为相反的数的值(x和-x)所分别对应的俩函数值。即同一条曲线上分处于y轴左右两侧，且距y轴等距离的两点的纵坐标！

　　刘志斌把f(x)与f(-x)这一对儿符号胡搅成两个相互之间关于y轴对称的不同函数，就搅出了这个违背函数基础知识的、矛盾的“f(x)=-f(x)”，这就非常的凸显出刘志斌胡搅乱弹的“刘志斌理论”是一套荒谬的、自相矛盾的 “二百五理论”！

　　刘志斌自以为有能力独创出有别与正统教育体系的、且能推翻正统数学理论的一套“刘志斌理论”！其实是刘志斌无知的表现！无知也就无畏！动不动刘志斌都要用他的“刘志斌理论”对正统学术机构编写的理论进行疯狂的胡批、瞎批！

引用 wanggq 的回复内容： 　　　

     用符号“y=f(x)”表示“y是x的函数”，已经足以表达因变量y与自变量x之间有映射的关系存在，而且x既可以代表正数，也可以代表负数。哪还用得着多此一举再添个符号“f(-x)”来表示“x的函数”！

1、如果 我用f(x)”表示一个已知函数，求一个函数，与已知函数f(x)的图像以y轴为对称，怎么办？是不是应该用f(-x)来表示“与已知函数f(x)的图像以y轴为对称的函数”；

2、如果 我用f(x)”表示一个已知函数，求一个函数，与已知函数f(x)的图像以x轴为对称，怎么办？是不是应该用-f(x)来表示“与已知函数f(x)的图像以x轴为对称的函数”；

3、如果 我用f(x)”表示一个已知函数，求一个函数，与已知函数f(x)的图像以原点o为对称，怎么办？是不是应该用-f(-x)来表示“与已知函数f(x)的图像以原点o为对称的函数”；

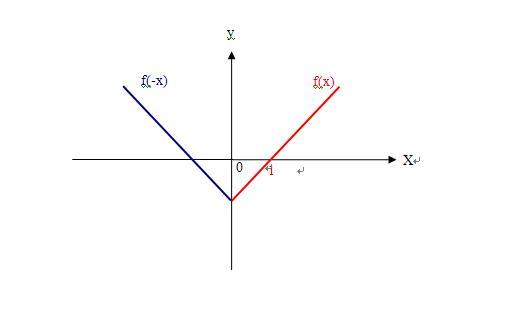
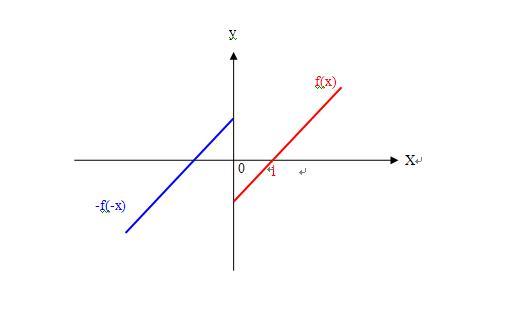
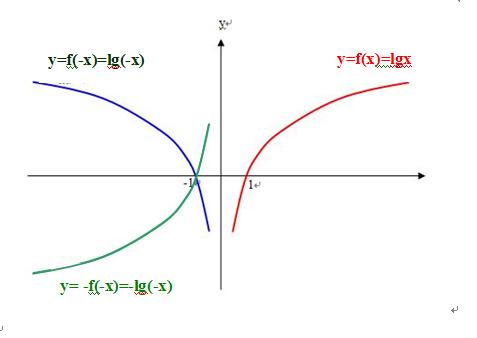
4、如果一个已知函数是lg(x)，求一个函数，与已知函数lg(x)的图像以y轴为对称，怎么办？是不是应该用lg(-x)来表示“与已知函数lg(x)的图像以y轴为对称的函数”；

5、如果 一个已知函数是lg(x)，求一个函数，与已知函数lg(x)的图像以x轴为对称，怎么办？是不是应该用-lg(x)来表示“与已知函数lg(x)的图像以x轴为对称的函数”；

6、如果 一个已知函数是lg(x)，求一个函数，与已知函数lg(x)的图像以原点o为对称，怎么办？是不是应该用 -lg(-x)，来表示“与已知函数lg(x)的图像以原点o为对称的函数”；

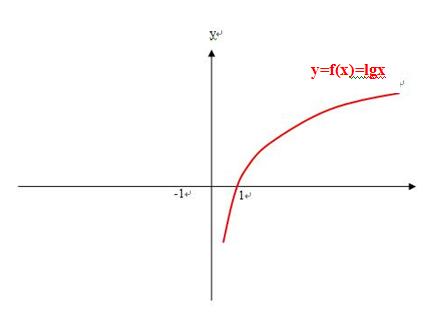
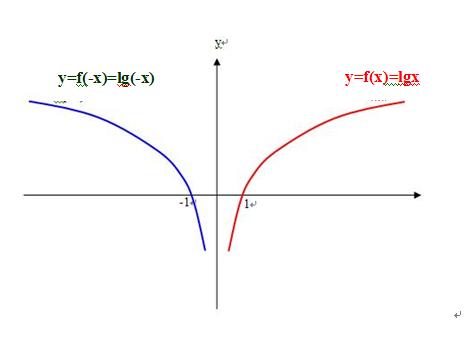
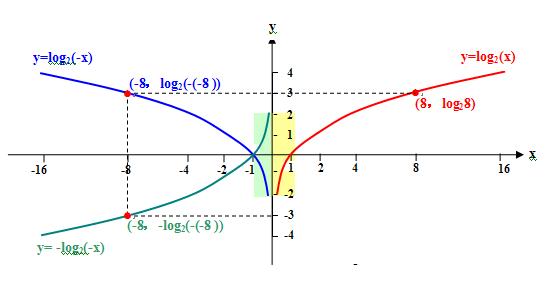
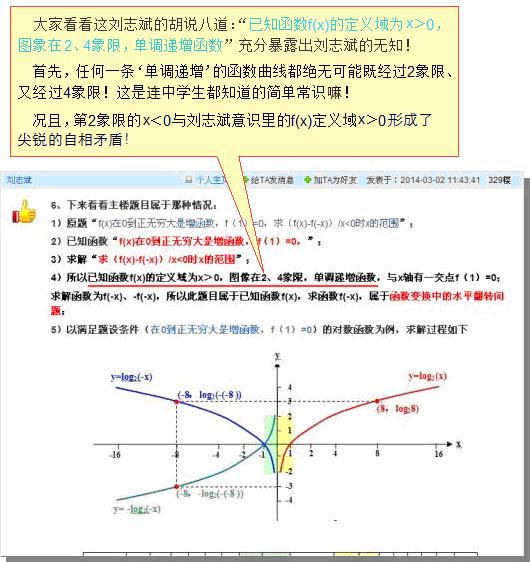
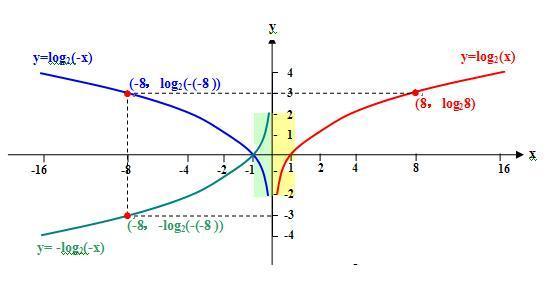
7、如果 我用log2(x)表示一个已知函数，求一个函数，与已知函数f(x)的图像以y轴为对称，怎么办？是不是应该用log2(-x)来表示“与已知函数f(x)的图像以y轴为对称的函数”；

8、如果 我用log2(x)表示一个已知函数，求一个函数，与已知函数f(x)的图像以x轴为对称，怎么办？是不是应该用-log2(x)来表示“与已知函数f(x)的图像以x轴为对称的函数”；

9、如果 我用log2(x)表示一个已知函数，求一个函数，与已知函数f(x)的图像以原点o为对称，怎么办？是不是应该用-log2(-x)来表示“与已知函数f(x)的图像以原点o为对称的函数”；

 wanggq 请回答以上问题？？？ 

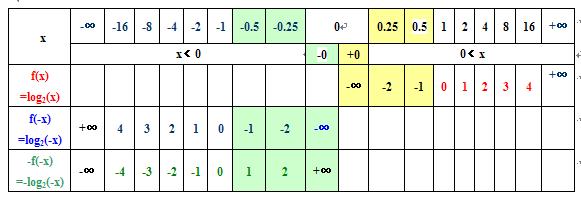
　　刘志斌提出以上一连串的问题，都表现出刘志斌对函数基本概念的无知！

　　首先，刘志斌不能正确解读出题目的实质意涵。正因为你刘志斌不能正确解读题目，所以你刘志斌才会有以上一连串的问题！

　　请注意：题目是“f(x)在0到正无穷大是增函数，f(1)=0，求(f(x)-f(-x))/x＜0时x的范围”。难道这题目中的f(x)是你刘志斌“已知”的函数吗？！不是！！

　　这题目中的f(x)是一个不确定的函数！“f(x)”只是一种简单表示函数的记号，它并不能让你刘志斌明确该函数关系中因变量依随自变量变化所遵从的对应法则，以及自变量可能取的值的范围！

　　题目的这一句‘f(x)在0到正无穷大是增函数’仅只能告诉你刘志斌该函数f(x)在右半开区间[0，+∞)上是单调递增的。并没有告诉你刘志斌该函数f(x)的定义域的全部范围之信息！

　　题目的这一句‘f(1)=0’也仅只告诉你刘志斌该函数曲线过(1，0)点。难道你刘志斌仅仅依据‘f(x)在0到正无穷大是增函数，f(1)=0’就能唯一确定出f(x)的定义域和对应法则？！该f(x)就成了你刘志斌“已知”的函数？！

　　刘志斌完全没看明白题目的核心内容：‘求(f(x)-f(-x))/x＜0时x的范围’！这一核心内容为同学们提供了一个非常重要的线索！

　　这一重要线索告诉同学们：题目所设的f(x)上有“(f(x)-f(-x))/x＜0”！所以，这“f(x)上有(f(x)-f(-x))/x＜0”也理所当然的该算是题目的一个条件！只是你刘志斌领悟不到这一“条件”而已罢了！但是，你刘志斌自己不能领悟到题目的这一条件，并不等于说题目就没有这一条件！

　　所以，我们可以总结出题目的全部条件总共有3条：

　　1)、f(x)在0到正无穷大是增函数，

　　2)、f(1)=0 ，

　　3)、f(x)上有(f(x)-f(-x))/x＜0 。

　　完全满足这3个条件的f(x)也不是唯一的一个函数！所以，题目所设的f(x)并不是“已知”的函数！

　　我们仅仅只是已知题目所设的f(x)必须满足这3个条件：1)、f(x)在0到正无穷大是增函数，2)、f(1)=0 ，3)、f(x)上有(f(x)-f(-x))/x＜0 ！

　　这个题目是让同学们选择一个既能满足：f(x)在0到正无穷大是增函数，f(1)=0 ，又能满足曲线上有(f(x)-f(-x))/x＜0 这种范围的函数f(x)，并求出你所选择的这个函数f(x)在(f(x)-f(-x))/x＜0时x的范围！

　　请注意，题目核心内容的这个不等式(f(x)-f(-x)) /x＜0中有一对儿记号“f(x)”和

“f(-x)”，它们都是指我们所选择的能够满足“在0到正无穷大是增函数，f(1)=0 ，且有(f(x)-f(-x))/x＜0 ”的这样一个函数f(x)上的俩“函数值记号”，是自变量在该函数定义域内取一对儿互为相反的数值(x和-x)所分别对应的俩函数值。

　　举例来说，我们根据题目条件，可以选择f(x)=3x^4-8x^3+6x^2-1 如图所示：

　　这个函数f(x)满足题目的全部条件：第1、f(x)在0到正无穷大是增函数，

第2、f(1)=0 ，    第3、有(f(x)-f(-x))/x＜0   !   

　　在这个选定的函数f(x)的定义域(-∞，+∞)上，让自变量取任意的一对儿互为相反数的值(x和-x)，按照选定的函数对应法则分别对应的一对儿函数值就是f(x)和f(-x) ! 

　　若：x= -1 ，则：-x=1  把这一对儿自变量值分别代入函数值记号f(x)、f(-x)

得：

　　f(x)=f(-1)=3(-1)^4-8(-1)^3+6(-1)^2-1 ＝16 

　　f(-x)=f(1)=3(1)^4-8(1)^3+6(1)^2-1 ＝0  　　 (符合题目的 f(1)=0的条件)  

　　注意：函数值f(x)与函数值f(-x)都是按同一个函数对应法则“f( )”来对应运算得到的！它们都是同一条函数曲线上的俩函数值！并不是象刘志斌那样瞎掰的两个对应法则不同的函数(关系)！

　　接下来，我们可以验证本例函数满足“有(f(x)-f(-x))/x＜0 时”：

　　(f(x)-f(-x))/x＝(f(-1)-f(1))/(-1)

　　　　　　   ＝(16-0)/(-1)

　　　　　　   ＝-16＜0    (符合题目条件：有(f(x)-f(-x))/x＜0 时)

　　我们可以证明本例函数f(x)在(f(x)-f(-x))/x＜0时x的范围是：{x│x∈R ，且x≠0 } .

　　对于正统教科书上关于“在研究讨论同一个问题时，相同的函数对应法则用相同的符号‘f( )’表示；不同的函数对应法则用不同的符号表示，譬如：用g( )与f( )相区别，或者，用φ( )与f( )相区别……”的理论，刘志斌就是难以接受，总是误以为教科书上的理论是‘谎言’！偏要自创出一套<刘志斌理论>来与教科书正统理论相抵触！刘志斌误以为：“对于一个任意的有确切定义的已知 函数f(x)， 就一定有一个函数 f(-x)与之对应存在”，并公然的对教科书的内容进行否定说：“任何情况下，f(x)与f(-x)都不是同一个函数上的俩函数值”……

　　看，刘志斌叨叨不休的问：“ 我用f(x)表示一个已知函数，求一个函数，与已知函数f(x)的图像以y轴为对称，怎么办？是不是应该用f(-x)来表示与已知函数f(x)的图像以y轴为对称的函数？”

　　y和x这两个变量之间的任何对应函数关系都可以用符号“f( )”来表示。请注意，符号“f( )”只是指出了因变量与自变量之间有函数关系这一事实，并不明确表示这个函数关系的具体对应法则是什么。

　　刘志斌你知不知道什么叫“已知的函数”？就单凭给你的一个符号“f(x)”，你刘志斌就知道它的相关两个变量之间的映射法则和定义域？！

　　你必须在知道了函数的自变量与因变量之间的映射关系及 定义域，之后才可以说你已知这个函数！

　　研究讨论实际问题而产生的函数的定义域是根据所考察的问题的实际意义来确定的。例如，某种茶杯的单价为 5元/个 ，售出茶杯的个数 x 与应该收进的货款y (元) 之间的映射关系就是一个函数关系：y=5x ，x∈N*  如果这个函数用符号“f(x)”来表示，那么就是：f(x)=5x ，x∈N* .

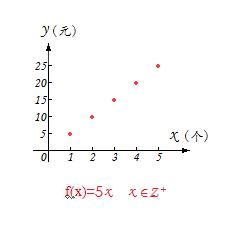
　　对于这茶杯个数与货款(元)之间成立的函数f(x)，难道你刘志斌可以用符号“f(-x)”来表示它，或者表示与它相互之间关于y轴对称的另一个函数吗？！不可以的！！

　　难道你刘志斌还一定能搅个“负的茶杯个数”出来？！显然，刘志斌理论中的：“对于一个任意的有确切定义的已知 函数f(x)， 就一定有一个函数 f(-x)与之对应存在”才是地地道道的“谎言”！

　　在数学中，有时不考虑函数的实际意义，而抽象地来研究用算式表达的函数。这时，我们约定：函数的定义域就是使算式有意义的自变量的一切实数值。也就是说，是这样的一些实数的全体，当用这种数代替算式中的自变量时，能够求出确定的因变量的实数值。

　　即便我们抽象的研究用算式表达的函数，刘志斌理论中的“对于一个任意的有确切定义的已知 函数f(x)， 就一定有一个函数 f(-x)与之对应存在”也仍然是错误的！！

　　一般地，如果a（a＞0，a≠1）的b次幂等于N，就是a^b=N，那么数b叫做以a为底N的对数，记作logaN=b 。

　　从定义可知，负数和零没有对数．事实上，因为a＞0，所以不论b是什么数，都有a^b＞0，这就是说不论b是什么数，N永远是正数，因此负数和零没有对数。

 　　刘志斌最初是把“对数函数f(x)=logax”误当做符合题目所有条件的函数f(x)，这是刘志斌违背正统数学理论“负数和零没有对数”的证据！

第1、

　　“对数函数f(x)=logax在x=0上无定义”刘志斌对这一知识没有搞清楚！居然认为对数函数的单调递增在[0，+∞)上! 

　　你刘志斌在这个右半开区间的0上，能搅出一个f(x)=logax的函数值f(0)来参与该对数函数值的增减比较吗？！对数函数f(x)=logax上不存在f(0)，难道你刘志斌不知道吗？！函数上不存在f(0)，那就不符合题设f(x)的单调递增区间“在0到正无穷大”的条件！

 第2、

　　“f(x)=logax的定义域{x│x＞0 }，是‘单边型定义域’”刘志斌对这一知识没有搞清楚！对于单边型定义域的函数来说，根本就没有谈“f(-x)”的前提！

 　　对一个函数谈“f(-x)”与“f(x)”的关系，其前提是该函数的定义域必须跨着0点左右两侧，其定义域上必须存在有互为相反的数(x和-x)的值！而对数函数f(x)=logax的定义域决定了它的自变量不可能取互为相反的数(x和-x)的值！所以，对数函数f(x)=logax上绝不可能出现“f(-x)”!!

 　　如果青年网友们误信了刘志斌自创的“刘志斌理论：对于一个任意的有确切定义的已知 函数f(x)， 就一定有一个函数 f(-x)与之对应存在” 那么，这些青年就会被刘志斌带入自相矛盾的混乱逻辑之泥潭！     

　　      待有空时再来！                                                                     

引用 wanggq 的回复内容：  　　

这充分说明：f(-x)与f(x)都是同一条曲线上的点！

1、wanggq 说“f(-x)与f(x)都是同一条曲线上的点！”这个说法就不妥了，就错了，

2、在讨论函数奇偶性时情况下 f(-x)与f(x)可以表示同一条曲线上的自变量取相反数时的两点的函数值！

3、在一般情况用f(-x)还可以表示“与已知函数f(x)的图像以y轴为对称的函数”；

4、在一般情况用用-f(x)还可以表示“与已知函数f(x)的图像以x轴为对称的函数”；

5、在一般情况用用-f(-x)还可以表示“与已知函数f(x)的图像以原点为对称的函数”；

6、看看wanggq 在下图中是不是胡说八道？

　　大家再看看这刘志斌的胡说八道：“已知函数f(x)的定义域为x＞0，图象在2、4象限，单调递增函数”充分暴露出刘志斌的无知！

　　首先，任何一条‘单调递增’的函数曲线都绝无可能既经过2象限、又经过4象限！这是中学生都知道的简单常识嘛！

　　况且，第2象限的x＜0与刘志斌意识里的f(x)定义域x＞0形成了尖锐的自相矛盾！

　　看看刘志斌的胡说八道　！！

　　刘志把同一条曲线说成是两个不同的函数f(x)和f(-x) 这就是刘志斌的胡说八道！

　　正统数学理论里说：符合同一个函数关系的所有点都在该函数曲线上；该函数曲线上的所有点都符合该函数关系！

　　这句话留给刘志斌去认真领会吧！

引用 wanggq 的回复内容： 　　　　　

……符合同一个函数关系的所有点都在该函数曲线上；该函数曲线上的所有点都符合该函数关系！

1、函数的表示方法有三种：

1）列表

2）图像

3）解析式

2、函数的图像：

1）符合函数解析式（或函数方程）的点都在该函数曲线上；

2）在该函数曲线上的点都符合函数解析式（或函数方程）；

3、下面是三个函数的三个解析式：

1）log2(x)；

2）log2(-x)；

3）-log2(-x)；

4、下面是三个函数的三个列表、及其三个图像曲线：

5、看上曲线图和列表：

1）三个函数解析式log2(x)、log2(-x)、-log2(-x)对应三个红、蓝、绿三条曲线；

2）红、蓝、绿三条曲线上各有一个点，分别是（8，log2(8)）、（-8，log2(-(-8))）、（-8，-log2(-(-8))）；

3）以上三点符合所在函数曲线的函数解析式：

6、 wanggq在1219楼 说：“函数曲线上由横坐标-8，纵坐标f(-8)所确定的点的坐标应当表示为(-8，f(-8))，并不可象刘志斌那样瞎胡搅，而搅出一个荒谬的位于y轴左侧平面内的点坐标(-8，f(-(-8)) !”，是不是自扇耳光！