昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
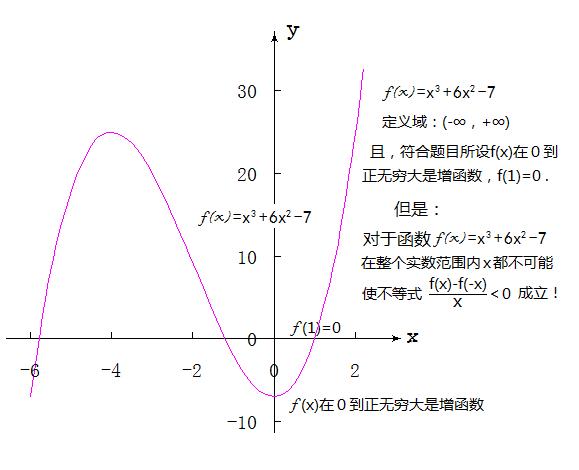
即便刘志斌从<烟雨朦朦>的发言内容中学到y=f(x)=x-1，x∈[0，+∞) 是满足
“f(x)在0到正无穷大是增函数，f(1)=0”的函数f(x)，但是，刘志斌却不知道：但凡是关于y轴成轴对称曲线的函数都不可能使不等式“(f(x)-f(-x))/x＜0”成立！
这就是刘志斌以y轴为对称轴，把y=f(x)=x-1，x∈[0，+∞) 的曲线对折到坐标平面的2、3象限，与原曲线形成的关于y轴对称的曲线：
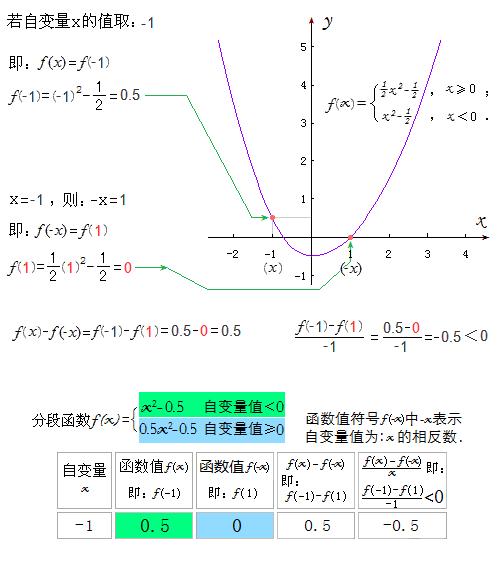
连中学生都知道，关于y轴成轴对称曲线的偶函数，若自变量取任意一对互为相反数“x”及“-x”时，分别对应的函数值“f(x)”及“f(-x)”是相等的！即对于偶函数，都有f(-x)=f(x)！
所以，f(x)-f(-x)=0 使不等式“(f(x)-f(x))/x＜0”不能成立！
刘志斌用关于y轴对称的曲线来作楼主题目的“解”的这一“荒谬”实在是太扎眼啦！
于是，刘志斌为了掩盖这一扎眼的谬误，又再胡搅一番，把y轴左侧的图形绕x轴对折翻转，胡搅出另一个“-f(-x)”来与y=f(x)=x-1，x∈[0，+∞) 形成关于坐标原点的对称图形，以期达到“蒙骗糊涂刘粉丝”的这一目的！
这就是刘志斌为楼主题目所做的另一个“解”：
刘志斌见没见着题目中的不等式“(f(x)-f(-x))/x＜0”?
不等式左边分式的分子“f(x)-f(-x)”可以看成“函数值f(x)”减去“函数值f(-x)”，这个等于0的“差”明显的使题目中的不等式不能成立！
“f(x)-f(-x)”也可以看成“函数值f(x)”加上“函数值-f(-x)”，这个“和”同样也是等于0的！
因为刘志斌的这个“-f(-x)”不正是刘志斌将“f(-x)”绕x轴对折翻转而得到的互为相反数的“函数值”吗！连初中学生都知道：减去一个“f(-x)”与加上它的相反数“-f(-x)”其结果是相等的！
所以，把“f(x)-f(-x)”当成“函数值f(x)”加上“函数值-f(-x)”的“和”，其结果也同样的使不等式“(f(x)-f(-x))/x＜0”不能成立！
现在老王来证明这个分段函数f(x)在0到正无穷大是增函数，且f(1)=0 .
证明：设x1，x2 是[0，+∞)上任意的两点，且0≤x1＜x2 。
1)、∵当x在[0，+∞) 区间上时，f(x)函数关系的对应法则为f2(x)= 0.5x^2－0.5
则，f(x1)＝0.5(x1)^2－0.5 ，f(x2)＝0.5(x2)^2－0.5
∴ f(x1)－f(x2)＝(0.5(x1)^2－0.5)－(0.5(x2)^2－0.5)＝0.5((x1)^2－(x2)^2)
又∵ 0≤x1＜x2 ∴ (x1)^2＜(x2)^2 即：f(x1)＜f(x2)
2)、当自变量值x=1 时，对应的函数值f(1)＝0.5(1)^2－0.5＝0.5－0.5＝0
所以，f(x)=0.5x^2－0.5 在“0到正无穷大”即[0，+∞)上是增函数，且f(1)＝0 。
早就解完了！楼主的这道高中数学题的正确答案之一就是老王在第5页贴出的答案：
设分段函数f(x)=f1(x) 当自变量取值＜0；f(x)=f2(x) 当自变量取值≥0 ，
当自变量取值＜0，即x在(-∞，0) 区间上时，f(x)函数关系的对应法则为：
f1(x)= x^2-0.5 ；
当自变量取值≥0，即x在[0，+∞) 区间上时，f(x)函数关系的对应法则为：
f2(x)=0.5x^2-0.5 。
此分段函数f(x)既符合题目“f(x)在0到正无穷大是增函数，f(1)=0,”之题设条件，又能使题目之核心部分的那个不等式“(f(x)-f(x))/x＜0”在除0之外的实数范围内有意义。
对于此分段函数f(x)来说，“(f(x)-f(-x))/x＜0”时x的范围是“除0之外的一切实数”！
既便这个简单题目的正确答案就摆在那些在所谓“兲朝”里做一天和尚撞一天烂钟的做事敷衍、得过且过、不求甚解、不求真知的人的面前，他也不认得这正确的答案，让刘志斌胡搅一下就给搅晕了头！误认为这道高中题目的正确“解”还没有解出来！
<紧接1390楼的内容>
分段函数f(x)=f1(x) 当自变量取值＜0；f(x)=f2(x) 当自变量取值≥0 ，
当自变量取值＜0，即x在(-∞，0) 区间上时，f(x)函数关系的对应法则为：
f1(x)= x^2-0.5 ；
当自变量取值≥0，即x在[0，+∞) 区间上时，f(x)函数关系的对应法则为：
f2(x)=0.5x^2-0.5 。
现在老王来证明该分段函数能让题目之核心部分中的那个不等式“(f(x)-f(-x))/x＜0”在x≠0的范围内具有意义。
证明：设“x”、“-x”是函数f(x)定义域内任意的一对互为相反数的自变量值.
1)、当x＞0时， 则：-x＜0 ,
那么，f(x)=0.5(x)^2-0.5 ；f(-x)= (-x)^2-0.5
则：f(x)-f(-x)=(0.5(x)^2-0.5)-((-x)^2-0.5)
=(0.5(x)^2-0.5)-((x)^2-0.5)
=(0.5-1)(x)^2
= -0.5(x)^2＜0
f(x)-f(-x)＜0，而x＞0，
即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立；
2)、当x＜0时， 则：-x＞0 ,
那么，f(x)=(x)^2-0.5 ；f(-x)=0.5(-x)^2-0.5
则：f(x)-f(-x)=((x)^2-0.5)-(0.5(-x)^2-0.5)
=((x)^2-0.5)-(0.5(x)^2-0.5)
=(1-0.5)(x)^2
=0.5(x)^2＞0
f(x)-f(-x)＞0，而x＜0，
即：不等式左边分式的分子、分母异号，不等式“(f(x)-f(x))/x＜0”成立。
所以，对于该分段函数f(x)有：自变量取除0之外的一切实数都能使不等式
“(f(x)-f(x))/x＜0”成立！
即：对于该分段函数f(x)来说，当(f(x)-f(-x))/x＜0时x的范围是“除0之外的一切实数”。
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
