昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
事实上，正弦函数关于原点对称的曲线仍然是它自己！
假设按刘志斌那样把“-f(-x)=-sin(-x)”当作“函数”绘出其曲线，再将其曲线与正弦函数f(x)=sinx 的曲线重叠起来，俩曲线是完全重合的！
这说明“-f(-x)=-sin(-x)”与f(x)=sinx 是同一个函数！
把-f(-x)重叠在f(x)上，因为俩曲线完全重合的缘故，我们只能看到重叠在上面一层的-f(-x)；
把f(x)重叠在-f(-x)上，因为俩曲线完全重合的缘故，我们只能看到重叠在上面一层的的f(x).
这充分说明，对于奇函数来说，关于原点对称的曲线完全是同一个函数！
通过f(-x)=cos(-x)和f(x)=cosx 俩曲线的完全重合，我们就很清楚的明白：仅用y=f(x)=cosx表达“y是x的余弦函数”就足以描述因变量y与自变量x的映射关系是余弦关系。根本就不再需要用“y=f(-x)=cos(-x)”来又一次的描述因变量y与自变量x的映射关系是余弦关系！
刘志斌不懂装懂的楞要用“f(-x)=cos(-x)”来当做有别于f(x)=cosx的另一个余弦关系是故弄玄虚，仿佛他刘志斌把简单的问题搅得愈复杂就愈显得他刘志斌更象什么“大师”似的！
其实刘志斌就是个不懂也要楞装出他“刘理论”深奥的二百五！
通过-f(-x)=-sin(-x)和f(x)=sinx 俩曲线的完全重合，我们就很清楚的明白：仅用 y=f(x)=sinx表达“y是x的正弦函数”就足以描述因变量y与自变量x的映射关系是正弦关系。根本就不再需要用“y=-f(-x)=-sin(-x)”来又一次的描述因变量y与自变量x的映射关系是正弦关系！
刘志斌不懂装懂的楞要用“-f(-x)=-sin(-x)”来当做有别于f(x)=sinx的另一个正弦关系是故弄玄虚，仿佛他刘志斌把简单的问题搅得愈复杂就愈显得他刘志斌更象什么“大师”似的！
其实刘志斌就是个不懂也要楞装出他“刘理论”深奥的二百五！
符号“f(x)”既可表达x的函数(即因变量与自变量的映射关系)，又可表达“函数的值”(即自变量取值为x时，因变量按照既定的映射法则f( )所得到的对应“函数值”)！对于这一点，当今的中学生在理解上都不会发生丝毫的困难！
根据句子的语境就可以正确判断出“f(x)”的意涵！例如句子“f(x)在0到正无穷上是增函数”很明显这“f(x)”就是指x的函数；不等式“(f(x)-f(-x))/x ＜0”也很明显“f(x)”及“f(-x)”就是指当自变量分别取互为相反的数值“x”及“-x”所分别对应的“函数值f(x)”及“函数值f(-x)”。
大家看嘛，这题目里只提及到一个函数f(x)，因变量f(x)对自变量的映射法则都是同一个法则“f( )”!
不等式“(f(x)-f(-x))/x＜0”中“f(x)”及“f(-x)”分别是当自变量取互为相反的数值“x”及“-x”时，按照同一个映射法则“f()”而分别得到的“函数值f(x)”及“函数值f(-x)”。同一个算式里同一个“f( )”表示的映射法则当然是“同一个映射法则”！
符号“y=f(x)”表示“y是x的函数”，自变量是x，因变量是y. 因变量也叫做自变量的函数。
有时图个简便，简洁用符号“f(x)”表示“x的函数”，自变量是x，因变量是
f(x)。
如果x代表函数定义域内的任意一个数值，则f(x)就代表按照既定的映射法则f()而得到的对应x值的“函数值”。
例如，函数f(x)=x^3+1
因为函数f(x)=x^3+1的定义域是全体实数，所以函数的自变量既可以取任意一个“x”值，又可以取其相反数“-x”的值。
设这个任意值x＝2，则对应的函数值f(x)=f(2)＝(2)^3+1=9；
若 x=2，则 -x= -2 ，自变量取值为-x 即取值为-2，
则，对应的函数值f(-x)=f(-2)=(-2)^3+1=-7 .
对于函数f(x)=3x ，有f(-x)=-3x ，即f(-x)= - f(x)；
对于函数f(x)=x^2 ，有f(-x)= (-x)^2=x^2，即f(-x)=f(x) .
一般地，对于函数f(x)：
1.如果对于函数定义域内任意一个x，都有f(-x)= - f(x)，那么函数f(x)就叫做奇函数。
2．如果对于函数定义域内任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。
3.如果对于函数定义域内任意一个x，f(-x)≠ - f(x)，且f(-x)≠f(x)，那么函数f(x)既不是奇函数，也不是偶函数！此种情况我们就说函数f(x)不具有奇偶性。
4.如果对于函数定义域内任意一个x，其相反数“-x”都落在定义域之外，那么该函数的值域内就绝无“函数值f(-x)” ! 所以，该函数f(x)也就绝无（关于y轴或原点的）对称性可言！该函数f(x)也当然的既不是奇函数，也不是偶函数！此种情况当然是函数不具有奇偶性的情况！
譬如：函数f(x)=logax 的定义域是{x│0＜x＜+∞}，x的相反数“-x”落在定义域之外，所以，函数f(x)=logax 绝无“函数值f(-x)”，即绝无“loga(-x)”！所以，对数函数是“非奇非偶”的函数！对数函数不具有奇偶性！
下面提供正统教科书上的例题作为证实老王在楼上的发言有正统理论依据的证明材料：
例如，判断下列函数是否具有奇偶性。
(1) f(x)=x^3； (2) f(x)=2x^4+3x^2； (3) f(x)=x^3+x^-(1/3)；(4) f(x)=x+１
解：
(1) f(-x) =(-x)^3= -x^3，即：f(-x)= -f(x)，所以，f(x)=x^3是奇函数。
(2) f(-x)=2(-x)^4+3(-x)^2＝2x^4+3x^2，即：f(-x)=f(x)，
所以，f(x)=2x^4+3x^2是偶函数。
(3) f(-x)=(-x)^3+(-x)^-(1/3)= -x^3-x^-(1/3)
= -(x^3+x^-(1/3))，即：f(-x)= - f(x)
所以，f(x)=x^3+x^-(1/3) 是奇函数。
(4) f(-x)= -x +1，-x +1≠-f(x)，且 -x +1≠f(x)，
所以，f(x)=x+1既不是奇函数，也不是偶函数。
“刘志斌理论”认为：f(-x)不是同一个函数f(x)中，自变量取一对互为相反数x、-x的值所分别对应的俩“函数值”之其中一个“函数值f(-x)”，而是跟原函数f(x)关于y轴成轴对称的另一个函数。
请注意1292楼这第(4)小题：判断函数f(x)=x+1是否具有奇偶性，教科书上给我们做的示范是：
解(4) f(-x)= -x +1，-x +1≠-f(x)，且 -x +1≠f(x)，
所以，f(x)=x+1既不是奇函数，也不是偶函数。
这个示范解里所用的“f(-x)”很明显不是跟原函数f(x)关于y轴成轴对称的另一个函数！“刘志斌理论”在正统教科书上这个示范解的面前暴露出“刘志斌理论荒谬、不靠谱”的本质！
举例来说，有函数y=f(x)=x+1 定义域是全体实数，所以，其自变量在定义域内存在互为相反的数x与-x ，当我们把这互为相反的数分别代入函数f(x)中，就分别得到“函数值f(x)”与“函数值f(-x)”
譬如，任意的设x=3，则 -x=-3
把 x的值代入函数f(x)=x+1 就能得到对应的函数值f(x)：
f(x)= f(3)=(3)+1= 4；
把 -x代入函数f(x)=x+1 就能得到对应的函数值f(-x)：
f(-x)= f(-3)=(-3)+1= -2，
当x=3时，对应的函数值f(x)=4，则对应于 -x=-3时的函数值f(-x)= -2
可见俩函数值不相等，就是 f(-x)≠f(x) ，且f(-x)≠-f(x)！
对老王所持的：不等式中“f(x)”和“f(-x)”的意涵为“函数值”这一观点，刘志斌极尽诋毁之能事，连篇累牍的对这一观点进行猛烈的胡批！
刘志斌诡辩，诋毁对手所持“f(-x)意为函数值”之观点，却居然反过来诬蔑老王有堂而皇之的把教科书上这：“当自变量取一对互为相反的数的值时，函数的值不变，就是f(-x)=f(x)”歪曲成错误和谎言！
事实上，正是刘志斌在竭力的诋毁正统数学理论中关于f(-x)是“自变量取一对互为相反的数x、-x的值时，其中‘-x’值所对应的函数值‘f(-x)’”的这一内容！
刘志斌颠倒黑白、混淆是非的诋毁和诽谤持不同观点的对手！刘志斌真是不要脸到了极点！
下面是函数f(x)=0.5x+2 的图象：
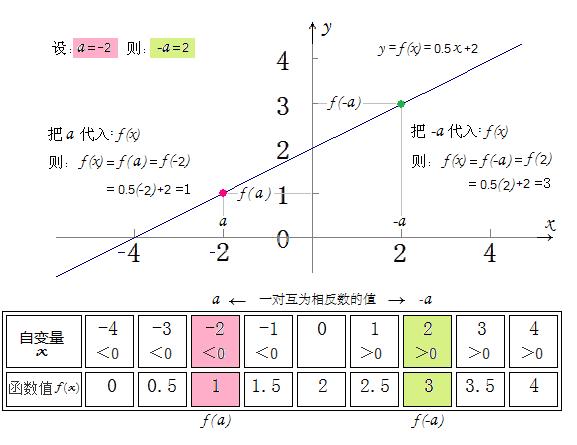
因为函数f(x)=0.5x+2 的映射法则是明确的，所以我们根本不需象刘志斌那样“解方程”或“解不等式”，一眼就看到该函数f(x)的定义域是{x│x∈R} 即一切实数。
如果 a = -2，则，-a = 2 .
把这两个互为相反的数分别代入函数f(x)＝0.5x+2，就分别得到：
“函数值f(a)”及“函数值f(-a)”
f(a) =0.5(-2)+2=1 ； f(-a) =0.5(2)+2=3 ．
那么，(f(a)-f(-a)) /a ＝(f(-2)-f(2))/(-2)＝(1-3)/(-2)=1
大家都知道，这是“代数运算式”！可刘志斌（伪“大师”）却不认得这是“代数运算式”！
从图象上，我们一眼就看到函数f(x)=0.5x+2 既不是奇函数，也不是偶函数。所以我们说函数f(x)=0.5x+2 不具有“奇偶性”。
从图象上，我们一眼就看到函数f(x)=0.5x+2 既不是奇函数，也不是偶函数。所以我们说函数f(x)=0.5x+2 不具有“奇偶性”。
如果我们用代数的方法来证明函数f(x)=0.5x+2 既不是奇函数，也不是偶函数，那么，其证明如下：
对于函数f(x)=0.5x+2 有 f(-x)=0.5(-x)+2= -0.5x+2 ,
∵ -0.5x+2≠-(0.5x+2) 即 f(-x)≠-f(x) ，∴函数f(x)=0.5x+2 不是奇函数；
∵ -0.5x+2≠ 0.5x+2 即 f(-x)≠f(x) ， ∴函数f(x)=0.5x+2 不是偶函数；
所以，函数f(x)=0.5x+2 既不是奇函数，也不是偶函数。
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
