昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
5、函数定义域的求法：做几道题，大家就知道是怎么回事
Ⅰ、抽象函数定义域的求法，常见题型有三种：
一，已知f(x）的定义域，求f(g(x））的定义域.
例1，已知f(x）的定义域为（-1，1），求f(2x-1）的定义域.
略解：由 -1<2x-1<1有 0<x<1
∴f(2x-1）的定义域为（0，1)
例，已知函数f(x)在0到正的无穷大，求函数f(-x)、-f(-x)的定义域
略解：-x＞0，x＜0。
∴f(-x)、-f(-x)的定义域为0到负无穷大，即x＜0。
二，已知f(g(x))的定义域，求f(x)的定义域.
例2，已知f(2x-1)的定义域为(0，1)，求f(x)的定义域。
解：已知0<x<1，设t=2x-1
∴x=(t+1)/2
∴0<(t+1)/2<1
∴-1<t<1
∴f(x)的定义域为(-1,1)
注意比较例1与例2，加深理解定义域为x的取值范围的含义。
三，已知f(g(x))的定义域，求f(h(x))的定义域.
例3，已知f(2x-1)的定义域为(0，1)，求f(x-1)的定义域。
略解：如例2，先求出f(x）的定义域为(-1，1)，然后如例1
有 -1<x-1<1，即0<x<2
∴f(x-1)的定义域为(0，2)
Ⅱ、求能使函数有意义的一切实数所组成的集合。
其主要根据：
①分式的分母不能为零
②偶次方根的被开方数不小于零
③对数函数的真数必须大于零
④指数函数和对数函数的底数必须大于零且不等于1
例4，已知f(x)=1/x+√（x+1），求f(x）的定义域。
略解：x≠0且x+1≧0，
∴f(x）的定义域为[-1，0）∪（0，+∞）
注意：答案一般用区间表示。
例5，已知f(x)=lg（-x^2+x+2），求f(x）的定义域。
略解：由-x^2+x+2 >0 有 x^ 2-x-2 <0
即-1<x<2
∴f(x）的定义域为（-1，2)
例，已知函数f(x)=lg(x)，定义域为x＞0，求函数f(-x)=lg(-x)的定义域。
略解：-x＞0，x＜0。
∴函数f(-x)=lg(-x)的定义域是x＜0；
Ⅲ、函数应用题的函数的定义域要根据实际情况求解。
例6，某工厂统计资料显示，产品次品率p与日产量x（件）（x∈N,1≦x<99）的关系符合如下规律：
x 1 2 3 4 … 89
p 2/99 1/49 2/97 1/48 … 2/11
又知每生产一件正品盈利100元，每生产一件次品损失100元.
求该厂日盈利额T（元）关于日产量x（件）的函数；
解：由题意：当日产量为x件时，次品率p=2/(100-x)
则次品个数为：2x/(100-x），正品个数为：x-2x/(100-x）所以T=100[x-2x/(100-x) ]-100·2x/(100-x)
即T=100[x-4x/(100-x) ],(x∈N且1≦x≦89)
给大家一个分段函数的例子，与主楼题目有点类似：
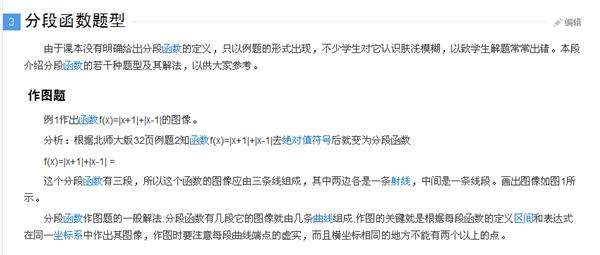
作出函数f(x) =│x+1│+│x-1│的图像
分析：根据北师大版32页例题2，知函数f(x) =│x+1│+│x-1│去绝对值号后就变成分段函数：
1）x+1≥0 x≥-1 则 │x+1│= x+1
x+1＜0 x＜-1 则 │x+1│= -x-1
2）x-1≥0 x≥1 则 │x-1│= x- 1
x-1＜0 x＜1 则 │x-1│= -x+1
3）x≥1 则f(x) =x+1+x-1=2x
x＜-1 则f(x) =-x-1-x+1=0
-1 ≤x＜1 则f(x) =x+1-x+1=2
这个分段函数分三段，所以这个函数的图像应由三条线组成，其中两条射线，中间一条线段组成；
x≥1 y=2x
-1 ≤x＜1 y=2
x＜-1 y=0
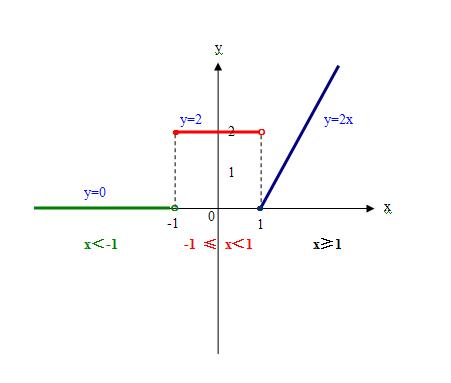
引用 wanggq 的回复内容：
……必然推出一个矛盾的： f(x)=-f(x)
即同一个自变量值x，按照同一个既定的映射法则f( ) 得出了两个互为相反数的“象”！这样，刘志斌理论与函数的映射观点相顶牛啦！
这说明，用f(-x)来表示函数是不妥的！会导致刘志斌理论的自相矛盾！
1、我们仔细看看 f(x)=-f(x)
1）同一个自变量值x；
2）一个的映射法则f( ) ，另一个映射法则-f( )，两函数值f(x)、-f(x) 互为相反数；
3）得出了两个互为相反的“象”！
2、这有什么矛盾？它表示两函数 f(x)、-f(x) 以x轴对称；
3、这个 wanggq 一贯喜欢睁眼说瞎话！
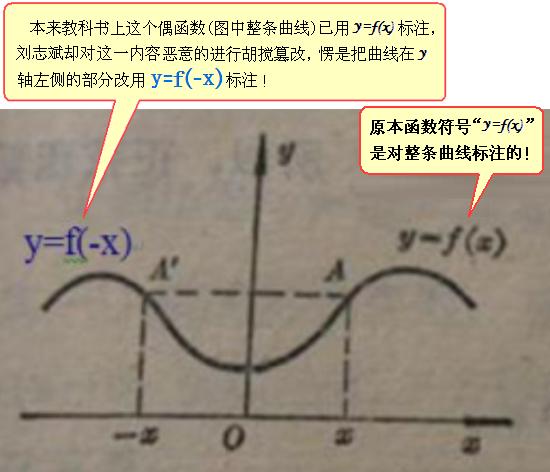
事实上，余弦函数关于y轴对称的曲线仍然是它自己！
假设按刘志斌那样把“f(-x)=cos(-x)”当作“函数”绘出其曲线，再将其曲线与余弦函数f(x)=cosx 的曲线重叠起来，俩曲线是完全重合的！
这说明“f(-x)=cos(-x)”与f(x)=cosx 是同一个函数！
把f(-x)重叠在f(x)上，因为俩曲线完全重合的缘故，我们只能看到重叠在上面一层的的f(-x);
把f(x)重叠在f(-x)上，因为俩曲线完全重合的缘故，我们只能看到重叠在上面一层的f(x).
这充分说明，对于偶函数来说，关于y轴对称的曲线完全是同一个函数！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
