昨天一道高中的数学题，我竟然不会做了 点击：21981 | 回复：1402
楼主最近还看过
为什么x=siny不是正弦函数y=sinx,x∈[-π/2,π/2]的反函数？
1、正弦函数y=sinx,x∈[-π/2,π/2]的反函数是反正弦函数x=sin^(-1)y,y∈[-1,1]，也即x=arcsiny,y∈[-1,1]。
对于x和y在定义区间上，两个函数中的x值相同，y值也相同。这样才互为反函数。
比如对于x=π/2和y=1，对于y=sinx,x∈[-π/2,π/2]是1=sinπ/2;
对于x=sin^(-1)y是π/2=sin^(-1)1，或π/2=arcsin1。
2、y=sinx,x∈[-π/2,π/2]的意思是角x（弧度表示）的正弦值是y；
而x=sin^(-1)y，y∈[-1,1]的意思是正弦值是y的，对应的角（弧度）是x。
这如同一对父子A和B，你说B是A的儿子，和A是B的父亲都对。可你要说A是B的儿子就不对了！
3、y=sinx如同B是A的儿子，而x=sin^(-1)y如同讲A是B的父亲。刘老师却告诉我们x=siny这就等于讲A是B的儿子,怎么可能是对的！
4、显然y=1时对于x=siny，得到的x=sin1=0.84147...显然不是π/2,因而x=siny根本不可能是y=sinx,x∈[-π/2,π/2]的反函数！
刘老师在1251楼如是说：
引用 wanggq 的回复内容：
对于偶函数f(x)来说，若用“f(-x)”表示与偶函数f(x)关于y轴对称的所谓的“另一个函数”实质上还是原函数f(x)! 因为它们的曲线是同一条曲线！映射法则是同一个法则“f()”！
1、当已知函数f(x)为偶函数时，必然符合条件f(x)=f(-x)；
2、函数“f(-x)”与函数f(x)关于y轴对称，则：f(-x)=f(x) ；
3、函数“-f(x)”与函数f(x)关于x轴对称，则：-f(x)=f(x) ；
4、函数“-f(-x)”与函数f(x)关于原点对称，则：-f(-x)=f(x)；
5、已知函数f(x)为偶函数时，必定有一个函数f(-x)也是偶函数，这两个函数的图像重合；
这说明刘老师在讨论函数奇偶性时，总将f(-x)看成是不同于函数f(x)的另一个函数。下面我们从理论和实例上分析其观点的荒谬性。
老王，和接受正常数学教育的人，奇偶函数的定义，一定类似于以下定义：
一般地，对于函数f(x)，假设x和-x同属于f(x)的定义域，如果函数值f(-x)、f(x)满足：
（1）f(-x)=f(x)，则称f(x)为偶函数；
（2）f(-x)=-f(x)，则称f(x)为奇函数。
以上定义明确表明：
（1）函数定义域必须关于原点对称，具有(-a,a)或[-a,a]（a>0,为有限数或无限大）形式，只有这样，才能保证x和-x同属一个定义域；
（2）奇偶函数是指某一个函数，如f(x)，而不是在两个函数之间，如函数f(x)和函数f(-x)；
（3）等式两边f(x)和f(-x)都是同一函数的函数值的比较，而不是两个函数函数值的比较。
我们一定记得,刘老师在讨论对数函数f(x)=loga(x),x>0时告诉我们f(-x)=loga(-x),x<0也同样可以叫对数函数，并且f(x)-f(-x)=loga(x)-loga(-x)，当x>0时等于f(x)=loga(x)，当x<0时等于-f(-x)=-loga(-x)。同时刘老师也告诉我们f(-x)和f(x)关于y轴对称。-f(-x)和f(x)关于原点对称。根据图象的对称性，我们能否得到loga(x)和loga(-x)既是奇函数又是偶函数呢？
这个思路似乎与函数的具体形式无关，是否可以得到f(x)和f(-x)既是奇函数又是偶函数呢？
我不敢说，因为刘老师会说我污蔑、造谣。刘老师亲自回答好吗？f(x)=loga(x)是不是奇函数或偶函数？
你的关于奇偶性到底是什么意思，怎么会涉及两个函数？
对1321楼内容的补充：
刘志斌为了掩饰自己把“f(-x)”判定为“函数”的谬误，所以，刘志斌不惜采用谎言“(虽有两函数f(x)=f(-x)或f(x)=-f(-x)，但不一定重合)！”来欺骗他的“刘粉丝”们！
刘志斌恶意捏造“y=-f(-x)=-(-x)^3”与“y=f(x)=x^3”俩曲线不能完全重合的这一虚假图象，欺骗他的“刘粉丝”们！（请注意：对奇函数y=f(x)=x^3 来说，刘志斌这个“-f(-x)=-(-x)^3”即“-f(-x)=f(x)=x^3”）
这是刘志斌捏造虚假信息的截屏证据：
老王把刘志斌这奇函数曲线放大来凸显“刘志斌理论”的欺骗性和荒谬性：
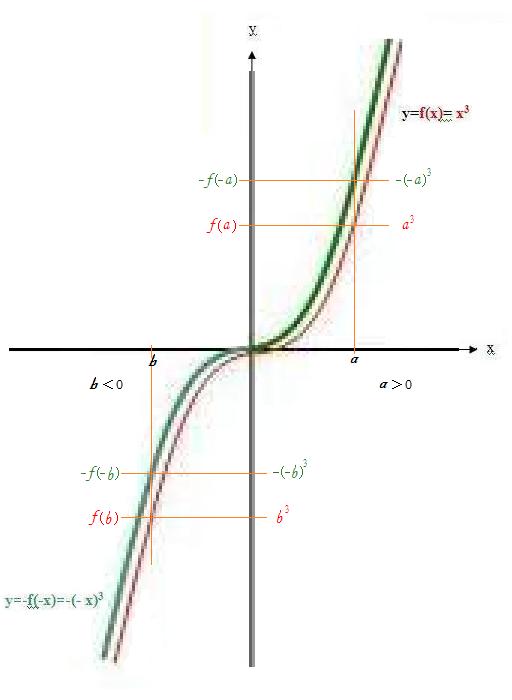
定理 奇函数曲线关于原点成中心对称图形；偶函数曲线关于y轴成轴对称图形。
根据这条定理，我们将奇函数曲线绕原点旋转180度，必定得到与原曲线完全重合的结果！
根据这条定理，我们将偶函数曲线绕y轴翻转180度，必定得到与原曲线完全重合的结果！
刘志斌总是热衷于自创出一套与正统理论相抵触的“刘志斌理论”！刘志斌公然在№1253楼散布“乱弹型刘理论”打胡乱说“(虽有两函数f(x)=f(-x)或f(x)=-f(-x)，但不一定重合)！”！
刘志斌完全不尊重正统科教机构编写出版的教科书上的正确理论！刘志斌极端自负的妄图要改写正统科教机构编写的教科书！
我们也可以将奇函数绕原点的180度旋转分解为两个绕轴翻转，即：绕y轴180度翻转+绕x轴180度翻转，即水平翻转+垂直翻转。这样经水平及垂直的两个翻转，其结果与绕原点180度旋转所得到的结果是完全相同的。
客观事实上，是否真如刘志斌胡搅的那样，“-f(-x)=-(-x)^3 曲线与f(x)=x^3 曲线虽有-f(-x)=f(x)，但不一定重合！”呢？！我们用铁的事实来否定刘志斌的这一胡说八道！
假如我们就依刘志斌那样把原曲线经水平及垂直两个翻转所得的绿色曲线看作是有别于原函数f(x)=x^3的另一个“函数y=-f(-x)=-(-x)^3”。
下面就是红色曲线y＝f(x)=x^3 与这个所谓的有别于原函数f(x)=x^3的另一个“函数y=-f(-x)=-(-x)^3”即绿色曲线重叠的两种情形：1、红色曲线叠在绿色曲线上面；2、绿色曲线叠在红色曲线上面：
把红色曲线重叠在绿色曲线的上面，因俩曲线完全重合的缘故，我们只能看到叠在上面一层的红色曲线（见左图）；
把绿色曲线重叠在红色曲线的上面，因俩曲线完全重合的缘故，我们只能看到叠在上面一层的绿色曲线（见右图）。
通过-f(-x)=-(-x)^3和f(x)=x^3 俩曲线的完全重合，我们就很清楚的明白：仅仅只用y=f(x)=x^3 来表达“y是x的函数”就足以描述因变量y与自变量x的映射关系为：“y是x的3次方幂”的这种关系。根本就不再需要用“y=-f(-x)=-(-x)^3”来重复的描述因变量y与自变量x的映射关系为：“y是x的3次方幂”的这种关系！
刘志斌不懂也要装懂的楞要用“-f(-x)=-(-x)^3”来当做有别于f(x)=x^3的另一个函数关系，纯粹就是故弄玄虚，仿佛他刘志斌把简单的问题搅得愈复杂就愈显得他刘志斌更象什么“大师”似的！
其实，刘志斌就是个不懂也要楞装出他“刘志斌理论”很深奥、很复杂，的这样一个“二百五”！
如果哪条曲线经水平及垂直两个翻转后与原曲线不能完全重合，即证明该曲线不是奇函数!
f(x)=x^3 是奇函数，那么它的曲线就一定是关于原点成中心对称的图形！奇函数f(x)=x^3的曲线经水平及垂直两个翻转，就必定是完全重合的！
刘志斌胡乱的涂鸦出一个曲线，也指鹿为马的把它叫做“y=f(x)=x^3”! 然后就胡说八道的宣称它虽有“-f(-x)=f(x)”的性质，但“-f(-x)”与“f(x)”不一定重合！
刘志斌这个所谓的“奇函数虽有-f(-x)=f(x)，但不一定重合”的曲线图分明就是自相矛盾！即“刘志斌的奇函数图形中-f(-a)≠f(a)”与“奇函数有-f(-x)=f(x)”自相矛盾！
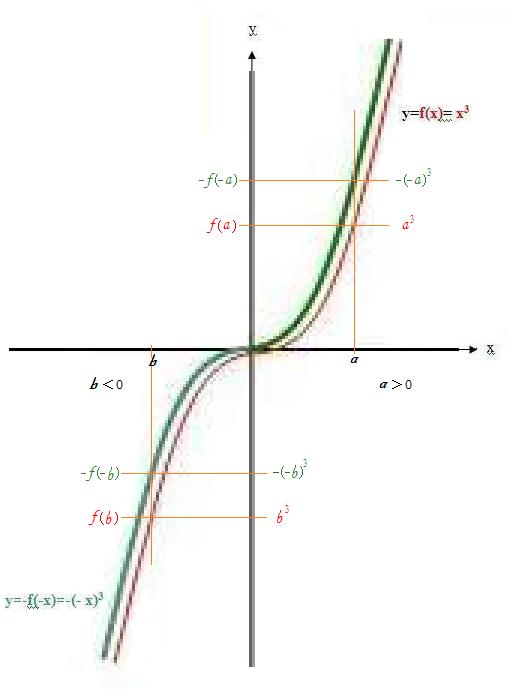
因为刘志斌的这个曲线图不真正是x的3次幂的曲线，所以我们若用y=f(x)=x^3 来检验时，曲线上的点的坐标数据不能与图形的样子相吻合！
我们姑且不和刘志斌计较这种不吻合，姑且把它的坐标分度认为是不均匀的刻度尺而忽略这种不吻合！
我们设a是自变量x的任意一个取值，且a＞0 ，
如果a=2 ，那么，对于红色曲线有 f(2)=(2)^3=8 ，
而对于绿色曲线有-f(-2)=-(-2)^3=-(-8)=8
这两个“8”应该是同一个纵坐标值吧？！即“-f(-x)=f(x)”! 刘志斌的曲线图中怎么就胡搅成：绿色曲线上的点(a ,-f(-a)) 即点(2，8)比红色曲线上的点(a，f(a))即点(2，8)高出那么大的一截来呢？
刘志斌怎样解释这“-f(-x)=8 和 f(x)=8 怎样的不能重合”？！刘志斌怎样解释这两个纵坐标值都同为‘8’时，还在同一坐标尺上相差一大截的距离？！
刘志斌理论中频频出现的这种“荒谬”的错误！证明了刘志斌就是个用荒谬理论来荼毒青年的“二百五”！
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
