昨天一道高中的数学题，我竟然不会做了 点击：22034 | 回复：1402
楼主最近还看过
6、寒湘子说“习惯上总将x看成自变量,y看成因变量。将x=arcsiny,写法变一下就是y=arcsinx。”错误，正确的是
1）正弦函数y=sinx，自变量x是角，因变量y是正弦值；
2）反正弦函数是x=siny，自变量x是正弦值，因变量y是角；
3）反正弦函数可表示为y=arcsinx，亦可以表示为y=sin^-1x；
4）将x看成自变量，y看成因变量，是发生在1）2）之间，而不是发生在“将x=arcsiny,写法变一下就是y=arcsinx。”
5）反函数y=arcsinx。是针对正函数y=sinx而言的！
6）反函数的反函数x=arcsiny，是针对反函数y=arcsinx而言的！
8、寒湘子说“y=arcsinx是怎么来的？是由x=arcsiny来”，是故意狡赖而已；
1）正函数是y=sinx，反函数是x=siny，可写作y=arcsinx，这不是数学运算的演变，这是对反函数x=siny的一个“文字语言描述”！
2）寒湘子煞费苦心，想玩个花样，实际上是对y=arcsinx的表示不知的缘故；
3）看看寒湘子1170楼怎么说的：“ 你怎么可以讲sin上方的-1丢了呢？这不丢人吗？我不懂数学都能发现明显错误，大师你会不知？”；
4）由原来认为是错的，发问怎么没有^-1，到编造谎言“y=arcsinx是怎么来的？是由x=arcsiny来”，足以表明寒湘子并非诚信辩论，而是真心狡赖捣乱！
不懂不要装懂！下面已讲得很清楚。
这是刘老师1165说的话：
1、我以为x=siny和y=arcsinx是一个意思；寒湘子认为不是一个意思，是哪个啥意思？
2、我举的例子 是错误的，说出来，我当众道歉！
我们知道刘老师认为正弦函数y=sinx将x,y两个变量位置变一下即：x=siny是反正弦函数。
我们知道函数和反函数变换是x,y表示的曲线不会改变，在笛卡尔坐标上，x轴始终是自变量，y始终是因变量或则函数。好了，对于y=sinx我们可以得到下列数值表：
x 0 90 180 270 360
y 0 1 0 -1 0
x为角度。那么无论正弦还是反正弦，这个表的对应数值不变，变得是函数关系，将x看成自变量，函数就是正弦，将y看成自变量，函数就是反正弦！
我们看看刘老师的函数x=siny，是什么？ 当y=1时，这是x应该等于90度，实数应为3.1415926.../2=1.5707963...这个数大于1，不管sin1是多少都不可能相等！事实上sin1=0.8415。刘老师你告诉我们这两个数相等吗？当然你还可以抵赖，我从没有指望你认错，只是想跟你讲一句，不要以为自己数学多好，瞧不起这个瞧不起那个，一把年龄，虚荣心也太高了吧！
对于y=sinx 的反函数x=arcsiny，在反函数变换里，这两个函数的x和y 永远相等！
比如x=pai/2=1.57... ,即90度角时y=1,我们将x,y带入就是1=sin1.57...，1.57...=arcsin1。但是你说反函数是x=siny,就应该1,57...=sin1，我们知道左边大于1，右边小于1.所以说x=siny是y=sinx的反函数必是错的！还在这胡搅蛮缠，不懂数学就不要谈，好像你在那嚷嚷，就表示你是对的？无知！
引用 寒湘子 的回复内容：
…… 我们看看刘老师的函数x=siny，是什么？ 当y=1时，这是x应该等于90度，实数应为3.1415926.../2=1.5707963...这个数大于1，不管sin1是多少都不可能相等！事实上sin1=0.8415。刘老师你告诉我们这两个数相等吗？……
1、反函数x=siny，即y=arcsinx，x是自变量正弦值，y是因变量角，举例说，x=1，y=90° =1,57...弧度；
2、反函数x=siny，即y=arcsinx，x是自变量正弦值，y是因变量角，举例说，x=0.8415 y=1弧度，
3、可以写成1=sin1,57...或者1,57...=arcsin1；
4、可以写成0.8415 =sin1或者1=arcsin0.8415 ；
5、寒湘子故意歪曲别人的发言，足以表明寒湘子并非诚信辩论，而是真心狡赖捣乱！
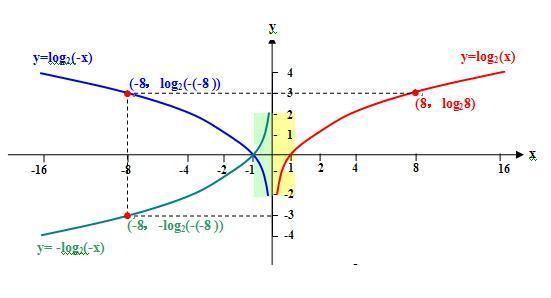
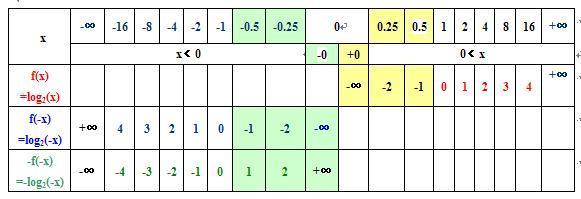
引用 寒湘子 的回复内容：…… f(x)-f(-x)定义域是空集，却可以求解(f(x)-f(-x))/x<0。……
1、求函数 g(x)=f(x)-f(-x)/x的定义域，
1）函数f(x)的定义域是x＞0；
2）函数-f(-x)的定义域是x＜0；
3）函数1/x的定义域是x≠0；
4）函数f(x)的定义域是x＞0、函数-f(-x)的定义域是x＜0和函数1/x的定义域是x≠0的“交集”为“空集”；
2，但是函数 g(x)=f(x)-f(-x)/x又是一个分段函数，
x＞0，g(x)=f(x)/x；
x＜0，g(x)=-f(-x)/x；
3、有什么问题？1和2有矛盾吗？
4、这样主楼题目有唯一正确的答案：
-1＜x＜0时，函数式（f(x)-f(-x)）/x=-f(-x)/x有意义，-f(-x)与x异号，-f(-x)/x=<0；
0＜x＜1时，函数式（f(x)-f(-x)）/x= f(x)/x有意义，f(x)与x异号，f(x)/x<0；
给大家一个分段函数的例子，与主楼题目有点类似：
作出函数f(x) =│x+1│+│x-1│的图像
分析：根据北师大版32页例题2，知函数f(x) =│x+1│+│x-1│去绝对值号后就变成分段函数：
1）x+1≥0 x≥-1 则 │x+1│= x+1
x+1＜0 x＜-1 则 │x+1│= -x-1
2）x-1≥0 x≥1 则 │x-1│= x- 1
x-1＜0 x＜1 则 │x-1│= -x+1
3） x≥1 则f(x) =x+1+x-1=2x
x＜-1 则f(x) =-x-1-x+1=0
-1 ≤x＜1 则f(x) =x+1-x+1=2
这个分段函数分三段，所以这个函数的图像应由三条线组成，其中两条射线，中间一条线段组成；
x≥1 y=2x
-1 ≤x＜1 y=2
x＜-1 y=0
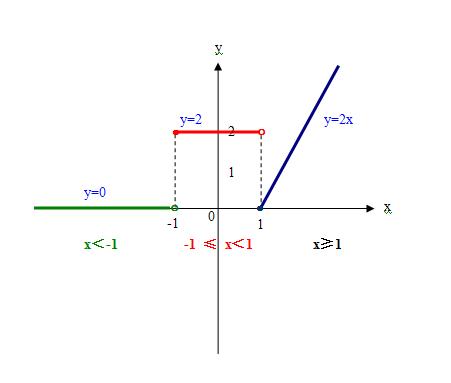
分段函数是指一个函数在其定义域内，对于自变量的不同取值范围，对应关系各不相同的函数。
刘志斌给大家的这个例子画f(x)=│x+1│+│x-1│的图象，是刘志斌胡乱搅出来的“错误解”！
大家看，把 f(x)=│x+1│+│x-1│写成分段函数的形式：
当自变量在左半开区间(-∞，-1 ]取值时，对应法则是y=-2x ,
例如：当x=-2 ,则f(-2)=-2(-2)=4；当x=-3 ,则f(-3)=-2(-3)=6； 但刘志斌却荒谬的把它胡搅成常函数y=0 ！
当自变量在右半开区间[1，+∞ )取值时，对应法则是y=2x , 但刘志斌却荒谬的把它胡搅成y=2x-2 ！
例如：当x=1 ,则f(1)=2(1)=2，但刘志斌的荒谬答案却是f(1)=2(1)=0 ! 显然，刘志斌画的黑色射线并不是“y=2x”！而实质上刘志斌画的是另一对应法则：y=2x-2 ！然而这另一对应法则y=2x-2 又与f(x)=│x+1│+│x-1│根本不搭界！
老王来纠正上述的刘志斌的谬误解！下面展示老王所做的正确解：
作函数f(x) =│x+1│+│x-1│的图象
分析：
1） x+1≤0 ，有 x≤-1 则 │x+1│= -x-1 ；
x+1＞0 ， 有 x＞-1 则 │x+1│ = x+1 ；
2） x-1＜0 ， 有 x＜1 则 │x-1│ = -x+1 ；
x-1≥0 ， 有 x≥1 则 │x-1│ = x -1 ；
3）当 x≤-1 则 f(x) =-x-1-x+1= -2x ；
当 -1＜x＜1 则 f(x) =x+1-x+1=2
当 x≥1 则 f(x) =x+1+x-1=2x
即：函数f(x)=│x+1│+│x-1│去绝对值符号变形为分段函数：
① x∈(-∞，-１]时 f(x)=f1(x)=-2x；
② x∈(-1，+１)时 f(x)=f2(x)= 2 ；
③ x∈[１，+∞) 时 f(x)=f3(x)=2x；
这个分段函数分三段，所以这个函数的图像由三段组成，左右两边各是一条射线，中间是一段水平(不含俩端点的)线段：
根据每段函数的定义区间和表达式在同一坐标系中作出其图像。作图时要注意每段曲线端点的虚实，因为横坐标相同的地方不能有两个以上的点。
注意：函数f(x) =│x+1│+│x-1│的图象是由三个区段组合而成的，左右两边各是一条射线：左边是由点(-1，2)发出，向左向上无限延伸的射线(如图中y= -2x所示)；右边是由点(1，2)发出，向右向上无限延伸的射线(如图中y=2x所示)。
这中间的一条水平线段的俩端点都是“虚点”（意即它的定义域不含俩端点，如图中红色线段y=2所示）。因为这俩端点所在的横坐标点已被俩射线的端点占用，而函数曲线上横坐标相同的地方不能有两个以上的点。
- 工控机和普通PC的区别
[11419] - 离心式水泵扬程H、流量Q、转速...[21312]
- 怎么判断三相电的三相？[13226]
- 交流接触器资料中AC-1 AC-2 ...[12218]
- 装机功率是什么啊？怎么计算？...[18034]
- 零线电流大于火线电流[20162]
- 请问星三角启动有时间继电器...[20478]
- 星三角启动电机烧毁原因请教...[12021]
- 48v电动车充电器12Ah和20Ah有...[12449]
- 『原创』如何制作动画教程[13614]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
