嘿嘿，人类是需要进步的！ 点击：6870 | 回复：467
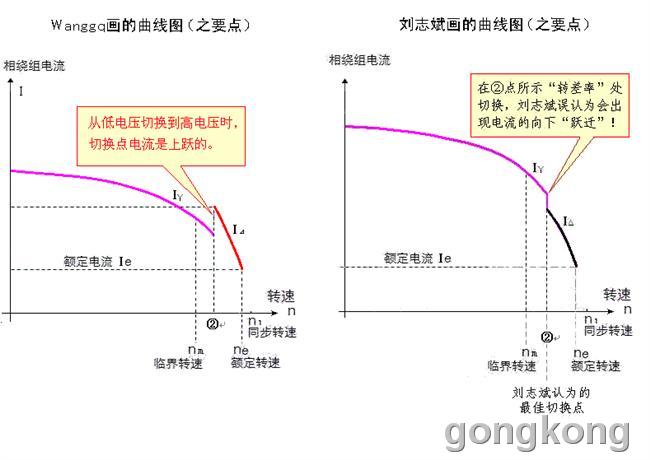
Wanggq与刘志斌就异步电机星/三角启动过程中有没有切换冲击电流的分歧产生争论。争论的焦点是：“由星接切换成角接，同一个切换转速点坐标处电流是向上变化的浪涌，还是向下变化的跌落？”的问题？！
Wanggq的观点是同一切换点转速坐标处，星接降额电流低，角接全额电流高。在切换点转速坐标处电流是向上浪涌的曲线；
刘志斌的观点是同一切换点转速坐标处，星接降额电流高，角接全额电流低。在切换点转速坐标处电流是向下跌落的曲线。
刘志斌还用文字加以说明“相同转差率情况下，电压高时电流小，电压低电流大；”难道刘志斌把这个事实掩盖得了吗？！
刘志斌的错误被对手指出来后，刘志斌就把他曲线中相同转差率前提下，由星接（大电流）向下“跌落”到角接（小电流）的这一错误，撇开不谈，把问题偷换成：电机负载运行时，负载运行功率不变，电压降低时电流增大。
其实，异步电机电流增大是因为电机转速的下降所至，转速下降即转差率增大。电机绕组的“等效阻抗”是随转差率增大而下降的，所以转速下降决定了绕组“等效阻抗”的下降，而等效阻抗下降得比较快，其阻碍作用下降的效果就比电压激励作用下降的效果更强势一些，因而把电压激励作用下降的效果给掩盖了！很多人就误以为电机电流变化的规律是电压低电流大。完全忽略了这个争论中的前提是：“相同转差率情况下”。
如果我们做这样一个实验：
找一个润滑良好的、额定角接的砂轮机（砂轮直径尽可能选择得大些，最好是还没有被磨削而变小了直径的新砂轮）因为砂轮的直径大，转动惯量就大！就象飞轮的性质：转速不易被改变。
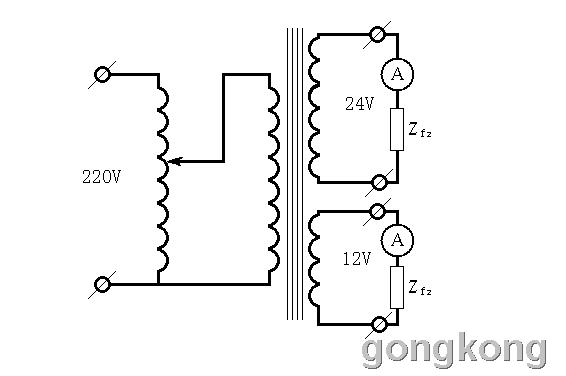
给砂轮机电机电路做一个星/角切换的电路，电机线电流的电路上串一个电流表。把砂轮电机启动起来后，我们可以随时由角接切换成星接或由星接切换成角接。
因为砂轮电机的转速不易被改变，所以，在电机正常运行中（但并不执行磨削任务）当我们切换电压，由全额高电压切换成降额低电压时，电机的转速来不及明显改变，我们就能从容的看到电流的下降；我们再把降额低电压切换成全额高电压，我们又能从容的看到电流的上升！这就证明：（相同转差率情况下，或近似相同转差率情况下）异步电机也是电压高则电流大，电压低则电流小！
异步电动机负载运行中，电压的降低，导致了电机转速的降低，而转速的降低则意味着“转差率”的增大，“转差率”的增大又直接影响电流的增大。这是一个“过程”。这个“过程”的概念，并不是“电压切换”的概念！
刘志斌先由一个“过程”的概念来混淆视听：“电压下降时，我们发现异步电机的电流是升高的”（这个“升高”就是指上述的一系列反应的“过程”），紧接着就把这个“过程”的概念拿来混淆他刘志斌臆造出来的这个不可能的事件：“电压突然下降，我们发现电流也会跟着电压的下降而突然增大”
电机转子以及它拖动的设备之旋转部件都是有一定“惯量”的，所以，电机转子的转速是不可能“突变”的。也就是说，电机的电流不可能跟着电压的突降而发生“突然”的增大！
电机愈小，其转子的“惯量”就愈小，则电流发生变化的“过程”就愈短，粗心的网友就愈容易产生“电流突然增大”的误觉而被刘志斌所忽悠。
我们这样来“实践”就能揭穿刘志斌的谎言！我们给一个功率不大的电机带一个惯量很大，但摩擦阻力及其它杂散损耗都很小的飞轮负载，用三相自偶调压变压器给电机提供可变电压的三相对称电源。先从低压缓慢升高到额定电压，在电机达到额定转速之后，如果突然调低电压。我们可以看到电流并不会跟着电压的突然降低而突然增大，相反，我们还会看到电流会因为电压的突然降低而发生减小！随即我们又将电压调回到额定电压，又能看到电流因电压的调高而发生增大！。
这里我们利用飞轮的“转速不能突变”这一性质，让我们能够在时间上很从容的观察到电压变化对电流变化的影响规律！有意识的减小“因转差率变化而带来的对电流变化的影响”，有助于我们正确地理解客观事物本来的原理！
实践是检验理论的标准，再向网友们给出另一个“判决试验”用来检验刘志斌理论：“相同转差率情况下，电压高时电流小，电压低电流大；” 以及 “当异步电机拖动同一个负载额定运行时，此时如果电压突降，我们发现异步电机的电流也会跟着电压的下降而突然升高，”是否为忽悠“糊涂童鞋”的荒谬理论！
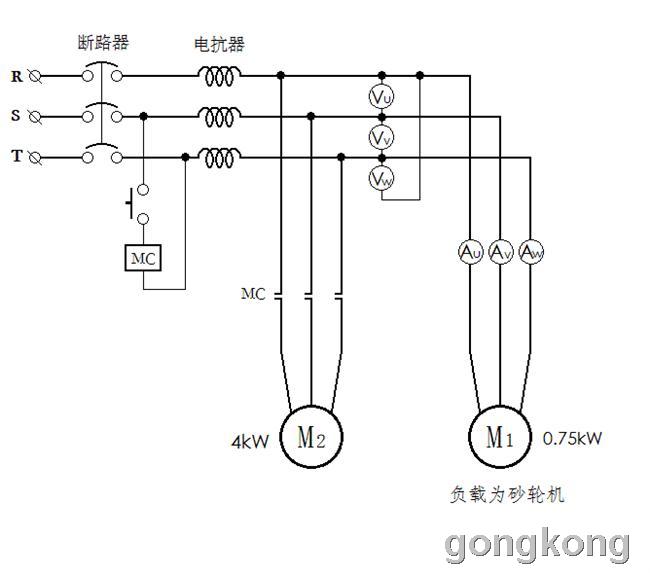
用有相等的同步转速的一大（7.5 kW）一小（0.75 kW）的两个异步电机通过连轴器链接起来，未施加电压的大电机其转子作为小电机的“惯量负载”正好适合实验要求（对0.75 kW 电机来说，7.5 kW 电机的转子就是一个惯量很大，但摩擦阻力和杂散损耗也不至于超过小电机额定负荷的“飞轮”负载）。
实验之前，先把一大一小的俩电机的相序搞成一致的（转向相同）。
<紧接楼下的内容>
- IAI电缸MODBUS通讯资料（中文...
[2960] - 漏电保护器的种类有哪些?[4559]
- 本人有三菱FX-TRN-BEG-C中文...[2153]
- 各种测功机技术参数[3190]
- 请问“垫片”用英语怎么说？[13591]
- 在 WinCC flexible 中如何实...[1965]
- plc中如何实现3hz的闪烁？（及...[3663]
- 条码打印机隔张打印的问题[3532]
- bit和bool的区别[2139]
- 编码器的作用？减速机和变频器...[5795]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
