嘿嘿,人类是需要进步的! 点击:9195 | 回复:467
我们用两个同一型号规格(所有参数相同)的异步电动机合拉一个负载,俩电机用连轴器链接起来(俩电机没有相对滑差,以确保俩电机是同一个转差率!),其中一个电机按额定接成角形接法:另一个降额接成星形接法。

两个异步电机可以在同时接入三相对称交流电源(请注意:先要把两个电机的相序搞成一致的,即同一转向。)
两个完全一样的交流电流表,分别串入两个异步电机的电源线中。
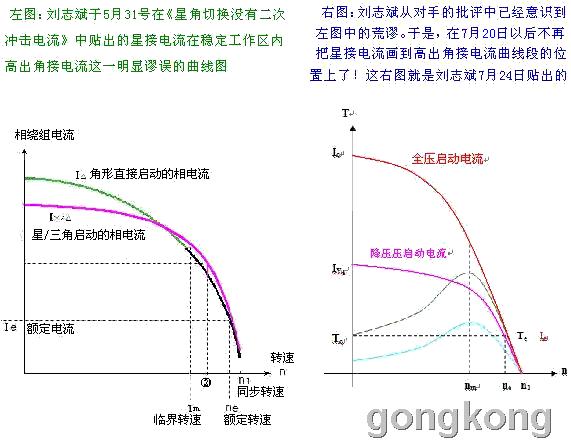
大家可以看到:在两个异步电机同时接入电源,启动过程中,以及负载运行中的任何一个速度、任何一个时刻都是全额电压(角接)所激起的电流大于降额电压(星接)所激起的电流。而且全额电流还是等于3倍的降额电流!
这个“实验”中因为俩电机的所有参数都一致,所以,我们可以将俩电机视同为同一个电机分别在施加全额、降额电压时线电流与转差率之间的关系。如果有网友对此有异议,那么,我们可以将两台电机的接法相互对换再实践一次,前后两次实践之间,间隔一两个小时以便让电机绕组的温度下降到环境温度而保证检验的公平。将同一个电机前后两次分别的角形、星形之接法所对应的电流进行比较,也能明确的告诉我们:相同转差率情况下,角接的线电流是星接线电流的3倍!(我认为,多数的网友是学过阻抗之“星/三角”等效变换的。当然是能够理解“相同转差率前提下,角接线电流等于星接线电流的3倍”这一客观现象的!)
我在百度查了一下,月球的质量约7350亿亿吨,合7.35×10^19 千克
月球在轨道上运转的速度约1023 米/秒 =1.023×10^3 米/秒
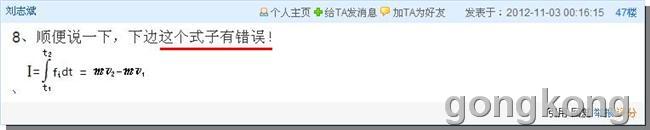
按学术界公认的动量之定义,月球在环地球的轨道上的动量为:
P=mv =7.35×10^19×1.023=7.51905×10^22 千克米/秒
=75,190,500,000,000,000,000,000 千克米/秒
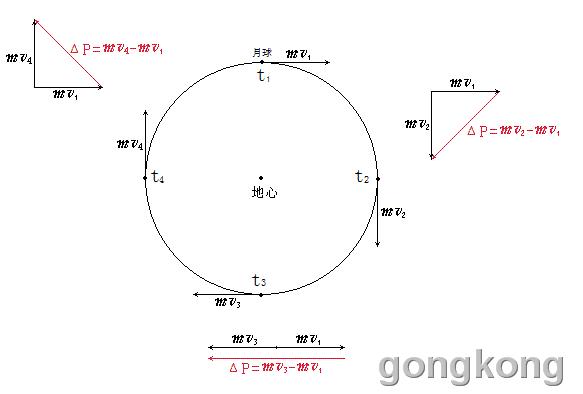
物体作圆周运动的瞬时速度的方向是圆的切线方向,它垂直于过该圆切点的半径。因此,月球在它圆形轨道上任何一点的速度在地球引力方向上的分量都为零。按照刘志斌理论这个分量v与月球的质量m的乘积就等于零。难道刘志斌认为月球在圆形轨道上的动量 P=mv = 0 千克米/秒 吗?!
很明显,这个刘理论是非常荒唐的!
- IAI电缸MODBUS通讯资料(中文...
 [2960]
[2960] - 漏电保护器的种类有哪些?
 [4559]
[4559] - 本人有三菱FX-TRN-BEG-C中文...
 [2153]
[2153] - 各种测功机技术参数
 [3190]
[3190] - 请问“垫片”用英语怎么说?
 [13591]
[13591] - 在 WinCC flexible 中如何实...
 [1965]
[1965] - plc中如何实现3hz的闪烁?(及...
 [3663]
[3663] - 条码打印机隔张打印的问题
 [3532]
[3532] - bit和bool的区别
 [2139]
[2139] - 编码器的作用?减速机和变频器...
 [5795]
[5795]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号










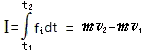

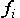 来表示。这种表示方法存在什么问题吗?!
来表示。这种表示方法存在什么问题吗?!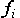 的下标 i 可以分别表示
的下标 i 可以分别表示 ,即符号
,即符号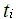 的力,这不就和符号
的力,这不就和符号 表示的意思是一样的吗!
表示的意思是一样的吗!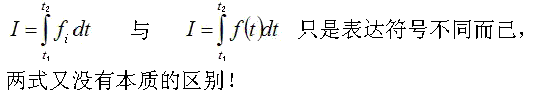

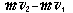












 工控网智造工程师好文精选
工控网智造工程师好文精选
