(感应异步电动机上)“转矩”与“转速”的因果关系 点击:12884 | 回复:319
楼主最近还看过
刘志斌回答不了自己设下悖论,就颠三倒四的说些胡话,自相矛盾!
刘志斌在60楼说坐标原点对应曲线上的点(启动转矩,零速度);在61楼反过来说坐标原点对应曲线上的点(0转矩,同步速度)
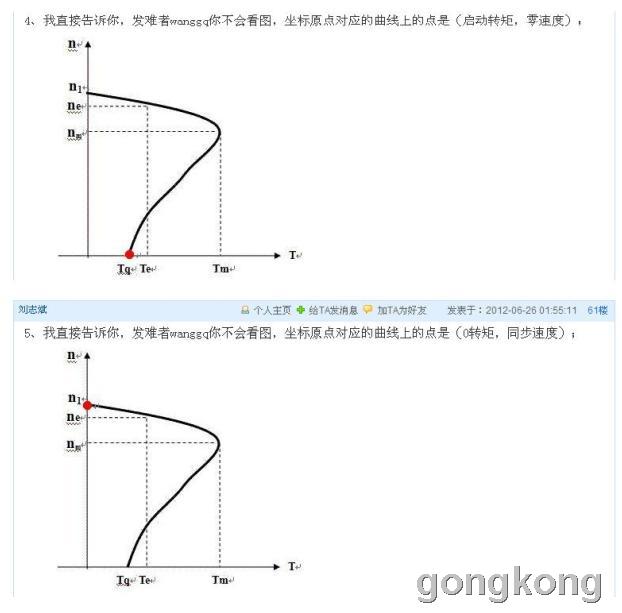
大家都知道:异步电机的“机械特性”曲线上所表达的是异步电机自身“转矩”与“转速”的相互关系,自然的这个“转矩”就是指异步电机的“电磁转矩”,而不是指负荷机械的“反抗转矩”!
虽然“反抗转矩”在量值上与电机“动力转矩”大小相等,但它们的方向却是相反的,所以它们不是同一个“转矩”!
刘志斌在回答异步电机“机械特性”曲线上“转矩”与转速的关系时,将电机的“动力转矩”与负载的“反抗转矩”相混淆。把电机的“动力转矩”的概念偷换成负载的“反抗转矩”。
我们要他回答:你刘志斌把电机的“动力转矩”看成是导致电机“转速变化”的原因,那么,你那个“零转矩”(当然是曲线上表达的电机转矩)何以能够导致电机的“转速”产生变化,从原本“非同步转速”变化成 “同步转速”的?
引用 刘志斌 的:
2、在电机机械特性曲线上,把转矩作为自变量,速度作为因变量有什么不妥?说“电机先有转矩才有的速度,转矩是因,速度是果”,有什么不对?

刘志斌这个“机械特性”曲线没有什么不妥!因为它以“曲线”形式来表达电机特性。作为“曲线”运用没有问题!我们也没有说过它有问题,是刘志斌小心眼儿自己揣测别人说他这个“机械特性”曲线有问题。
虽然刘志斌的“机械特性”曲线没有问题,但是,该曲线是不能看成“电机转速对转矩的函数图象”的!不能象刘志斌那样误认为:在电机机械特性曲线上,可以把转矩作为自变量,速度作为因变量来理解!
刘志斌误认为“在电机机械特性曲线上,可以把转矩作为自变量,速度作为因变量来理解”的原因是刘志斌误以为“机械特性”曲线与“转矩-转速”函数是“互为反函数”的。
刘志斌之所以误认为“机械特性”曲线与“转矩-转速”函数“互为反函数”,是因为刘志斌误以为“在某个变化过程中,两个相依变化的量,可以不分变化之主从、不分变化之因果,随便哪一个变量都可以定义为自变量,或因变量”
据新版教科书对“函数”的定义:
对于自变量 x 在定义域内的每一个值,函数 Y 都有唯一的值与它对应。
若以函数的观点看上面的那个“机械特性曲线”则出现有与函数定义不符的情况:对于“自变量T”在大于“Tq” 到小于 “Tm” 之间的每一个值,函数n 的值都不是唯一的值与自变量T相对应!
从数学角度看,一个函数的反函数并不一定有相同的曲线(不考虑“旋转”、“翻转”的差别)!
譬如:函数 Y = sin x 的定义域是:-∞ 到 +∞ ;值域是:-1 到 +1
其反函数 Y= arc sin x 的定义域是:-1 到 +1; 但是,其值域却不是这个:【 -∞ 到 +∞ 】
Y= arc sin x 的值域是: -π/2 到 +π/2 这个值域限制为:【 -π/2 到 +π/2 】 就是冲函数定义而做的限制!
两个互为反函数的函数图象,并不是象刘志斌认为的那样:把某条曲线随便横放或竖放都符合函数的规范!
这个曲线是正弦函数 Y =sin x 的图象:
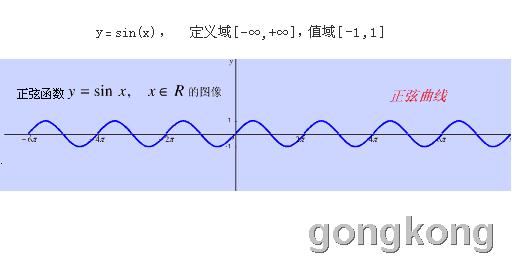
并不是该曲线竖着放也可以说成是正弦函数的反函数图象的!下面这个把正弦曲线竖着放的图象并不符合函数图象的规范!
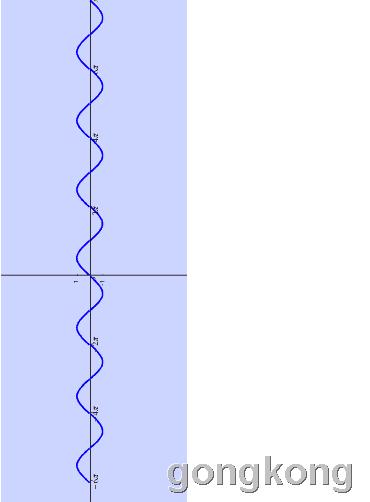
而符合反正弦函数 Y = arc sin x 规范的的函数曲线是下面这个样子的:
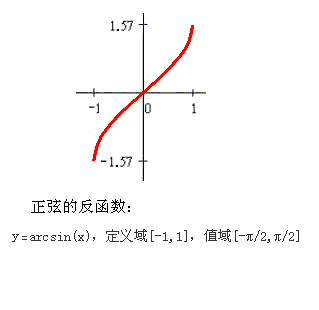
刘志斌 就是搞不明白:
2、在电机机械特性曲线上,把转矩作为自变量,速度作为因变量有什么不妥?说“电机先有转矩才有的速度,转矩是因,速度是果”,有什么不对?
现在我来说明为什么在电机机械特性曲线上,把转矩作为自变量,速度作为因变量不妥;以及为什么说感应异步“电机先有转矩才有的速度,转矩是因,速度是果”,不对!
其一:不符合学术界对函数的定义!
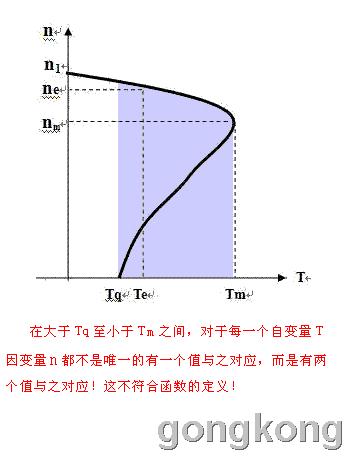
在其它所有条件相同的前提下,某个变化由一个原因(自变量)引起的结果(因变量)只能是一个结果,不可能它既是甲种结果,又是乙种结果!
所以,感应异步电机的“转速”才是原因,作自变量;而感应异步电机的“转矩”则是因“转速变化”而相应变化的量,是“转速变化”的结果,作因变量。这才是符合实情,且符合函数规范定义的。但是我这个说法并不是在说“机械特性曲线”不规范,作为“曲线”应用可以不讲究自变量、因变量的区别,但作为“函数”分析,则应该遵守“函数”的规范定义,必须讲究自变量与因变量的因果关系!
其二:刘志斌把感应异步电动机的“电磁转矩”看成是导致异步电机转子速度变化的原因不符合客观事实!

刘志斌是针对这一条"异步电动机机械特性曲线"所说的"电机先有转矩才有的速度,转矩是因,速度是果"(大家都很明白,刘志斌说的"先有转矩"这一句子中转矩的概念是明确的指曲线上所示的"电机转矩"而不是他后来改口的"负载转矩"!)。我们先假定刘志斌的这一论断成立。按照刘志斌提出的这个“因果关系,则必然推出刘志斌这一论断与客观事实相矛盾的结果来:由于电动机先有了转矩,在这个“电磁转矩”作用下电机才产生的速度,速度的变化(即:“加速度”)方向就必然是与电机的“电磁转矩”的方向一致的。但是,刘志斌的曲线上“同步转速”至“临界转速”的这一段却表现为随“转矩”的增加而出现了“转速”的下降!曲线上这一段速度变化(即:“加速度”)方向与电机“动力转矩”的方向相反充分证明刘志斌的论点:“电机先有转矩才有的速度,转矩是因,速度是果”是错误的!
这充分说明:异步电机的“动力转矩”并不是这个转速下降的原因,而电机“转速的下降”也并不是“动力转矩增加”的结果!而相反的,异步电机“转速变化”才是因,异步电机的“转矩变化”才是果!
引用 刘志斌 的:
2、在wanggq 发难时,他认为只有“感应异步电动机上”的“转速是因,电磁转矩是果”;
3、其实所有电动机上都是“转速是因,电磁转矩是果”;

在“转速是因,转矩是果”的前面加上“感应异步电动机上”这样的限制,是因为我看到刘志斌黔驴技穷,开始耍文字游戏了,为了防止刘志斌抠字眼,钻空子,才加上这几个字的!
刘志斌的“3、其实所有的电动机上都是‘转速是因,电磁转矩是果’”足以说明刘志斌自己已经知道他刘志斌针对感应异步电动机所作的论断:“电机是先有转矩才有的速度,转矩是因,速度是果”是一个谬误!但是,刘志斌仍然还不知道他自己又陷入了另一个谬误的泥潭里!
刘志斌又陷入了一个什么谬误泥潭?!
这又一个谬误就是刘志斌的“3、所有的电动机上都是转速是因,电磁转矩是果”。
其实,有的电动机上,并不是“转速是因,电磁转矩是果”!譬如:步进电机。
直流电动机、交直两用串激式电动机都并不是先有了转速,才有的转矩,而它们是先有了转矩,才有了电机的转速。因为它们的转子电流是电源直接提供的。并不象感应异步电机那样靠“转差”来产生转子电流!
我们叫刘志斌回答根据他自己说的“2、那个轴作速度轴,都是一样的” ;“2、在电机机械特性曲线上,把转矩作为自变量,速度作为因变量;” “电机先有转矩才有的速度,转矩是因速度是果,”怎样解释刘志斌“特性曲线”上作为变化之因的“零转矩”何以能够导致电机从其它转速变化到同步转速这个结果?
假如刘志斌说的“转矩是因速度是果”成立,那么,请刘志斌解释这个先有的零转矩又如何能够使电机转子获得“才有的同步转速”?!刘志斌回答不了这个问题,就顾左右而言他!东拉西扯的说什么“坐标原点对应曲线上的点(启动转矩,零速度);坐标原点对应曲线上的点(0转矩,同步速度)”
难道刘志斌这样东拉西扯的回答,就算解决了“零转矩导致了电机转子从非同步转速变化到同步转速”的问题吗?!东拉西扯回避该问题就算刘志斌有本事吗?!
对于刘志斌搞的用转矩作自变量,速度作为因变量;则:在坐标原点的自变量就是零转矩。用函数的概念看刘志斌的曲线上对应零转矩的点是:因变量为“同步转速”的点,这一点的坐标是(零转矩,同步速度)。
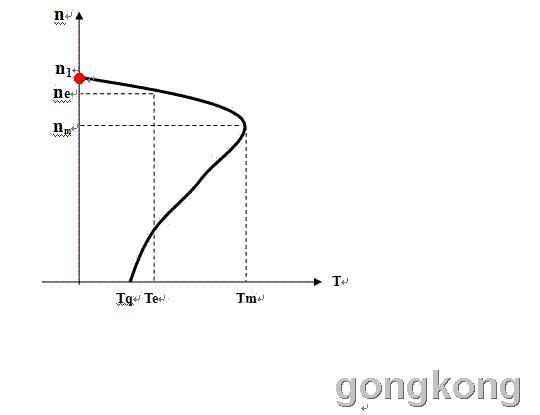
刘志斌能解释他的这个同步速度是如何被这个零转矩作用而“才有的”吗?!一个零转矩能够让原本不是同步转速的转子变速为“同步转速”吗?!
刘志斌所谓“才有的”是指电机转子的转速原本不是“同步转速”,是因为有了一个“零转矩”的作用,才导致了电机转子的转速变化为“同步转速”!
电机转子是有“转动惯量”的,设这个“转动惯量”为 I , 转子原本的速度与“同步转速”有一个差值:△ω
根据<转动定律>: M=Iβ 可得: M=I* (△ω /△t) , 或 M△t=I△ω
当M为零时, 等式 I△ω = M△t 的右边即为零,理所当然等式左边也必然为零!即:△ω 必为零!
△ω 为零,说明了零转矩决不可能会使电机转子的转速发生某一“非零”量值的变化!
说明了刘志斌把异步电机的转矩当作自变量是一个谬误!
引用 wanggq 的回复内容:
……刘志斌认为是所有异步电机特性标准的他那个“转矩是因,速度是果”的曲线图中,在坐标原点的转矩是“零转矩”,而这个“零转矩”却对应着坐标纵轴上异步电动机的同步转速。……
wanggq 的这个表述不够清楚吗?刘志斌把他的曲线说成也是函数。而把电机的“转矩”说成是这个函数中的自变量。一般自变量是表示在坐标横轴上的,因变量(也就是自变量的函数)是表示在纵轴上的。横纵坐标轴的交点就是零点。自变量(转矩)在这个零点位置上的值就是“零转矩”!这有错吗?对于自变量的这个“零转矩”,因变量(转速)有一个值与它对应。这个与自变量“零转矩”对应的值就在通过零点的垂直于横轴的直线上,这条直线就是纵坐标轴。说“这个“零转矩”对应着坐标纵轴上的‘同步转速’”有错吗?!
发难者刘志斌,不愧是发难者,发难说:“去问问小学6年级学过“位置”的表示法的学生,坐标原点是(零转矩,同步转速)?!”
刘志斌不会看图!把自变量(零转矩)对应的因变量(同步转速)看成了“零转速”,同时又犯糊涂的、自相矛盾的看成了“启动转矩”!刘志斌怎么这样愚的在函数问题上用自变量对应自变量?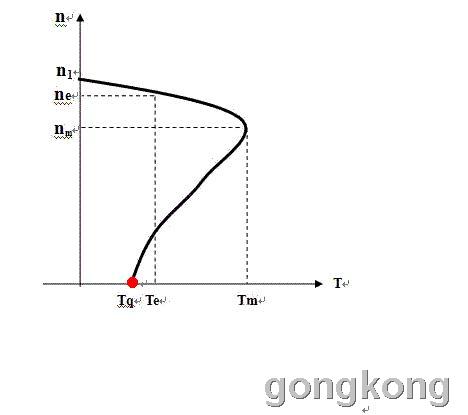
- 软起动实现电机正、反转控制功...
 [1092]
[1092] - 关于工控机上的软驱改造心得
 [1150]
[1150] - [转贴]六款主流视频会议软件...
 [1305]
[1305] - s7-200plc在组态王中的数据读...
 [1866]
[1866] - 求助,WINCC flexible连接以太...
 [1563]
[1563] - 请教各位高手:基恩士PLC打开...
 [4791]
[4791] - 中国工控网第500,000个注册用...
 [5299]
[5299] - 全世界懂中文的人都会回的一...
 [1553]
[1553] - S7-200 PLC EM231模拟量输入...
 [1941]
[1941] - 根据滚珠丝杠相关参数如何求...
 [1373]
[1373]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号



















 工控网智造工程师好文精选
工控网智造工程师好文精选
