关于电机“星 / 三角启动”过程的问题 点击:7371 | 回复:276
楼主最近还看过
引用 刘志斌 的:
1、“静负荷”、“动负荷”是个人的一种理解;
2、学习一下牛顿三定律,用大家知道的物理概念来描述运动控制的参数;
3、个人的理解往往有主观上的错误和偏差,失去和大家交流的共同语言或基础!
我对电机使用说明书指的“静负荷”和“动负荷”是这样理解的:
“静负荷”是负载没有明显“角加速度”时对动力所呈现出的“反抗转矩”。也可以理解成负载的角速度没有急速改变的前提下对电机呈现的“反抗转矩”。
“动负荷”是负载“角速度”在电机输出的“动力转矩”作用下急速提高的情形下对电机呈现出了在原有“不加速转动”之负荷基础上再加上由于加速而额外多出的“反抗转矩”,两部分叠加起来的负荷。
牛顿第三定律是作用力和反作用力同时产生,同时消失。作用力和反作用力作用在同一直线上,大小相等,方向相反。
这“动力转矩”和“反抗转矩”的关系跟作用力与反作用力的关系相似,是一个道理。“反抗转矩”与“动力转矩”同时产生同时消失,“反抗转矩”和“动力转矩”作用在同一转轴上,大小相等,方向相反。
设备在其动力转矩拖动下转动,总是要产生一个“反抗转矩”与“动力转矩”相抗衡。(这是根据牛顿第三定律得出的结论)
所以,电机的转速不是由电机一方单独决定的。电机的“转矩对转速的函数曲线”其横坐标是电机的“转速”,而不是“时间”。它不是电机的“转矩对时间的函数曲线”,也就不能象刘老师那样单从“转矩对转速的函数”曲线上某段的斜率来判断电机是否“很快进入稳定工作区”!
引用 刘志斌 的:
3、看看楼主的图,同一个负载,怎么出现两个转矩?全压启动后的负载转矩大于降压启动后的负载转矩2倍?
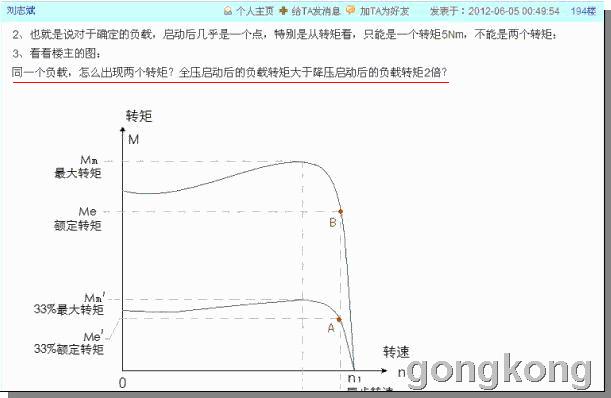
只能说刘志斌看不懂别人表达的意思!
图中是两个不同幅度电压分别对应的“转矩对转速的函数”两条曲线。其中较高位置的一条曲线是电机在额定电压下对应的“转矩-转速”曲线;较低位置的一条曲线是电机在58%幅度的电压下对应的“转矩-转速”曲线。
你刘老师不是认为冲床、剪板机之类的设备上额定角接的电机仅凭一段足够长时间的星形接法(给电机只施加58%幅度的电压)就可以完成把设备的转速提高到“额定转速”吗,你不是用了一条如下图的“电机的机械特性”曲线来说明这个“启动全过程”的吗:
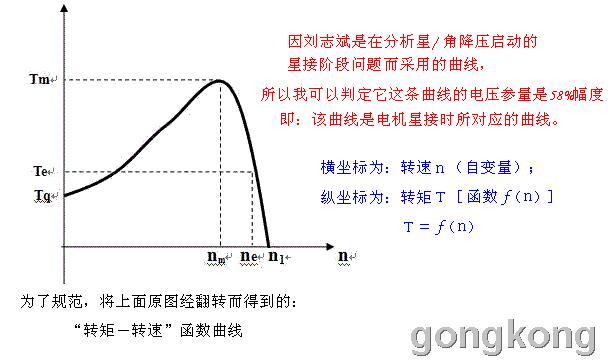

我认为:在冲床、剪板机之类设备上合理配置的拖动电机,仅58%幅度的电压下是不可能单凭其拖动电机的力量把设备拉转到“额定转速”的!,为了讲出这个结论的理论根据,我才把全额电压和58%幅度的电压分别对应的两条曲线画到同一个坐标系里来分析说明用58%幅度的电压不可能完成需全额电压才能完成的启动阶段(指“星 / 三角启动”之后期角接阶段)。
“B点转矩”是额定电压、额定转速所对应的转矩,用Me表示。在合理配置动力的方案设计中,它是“根据额定负荷需求来决定选择电机转矩”的指标。
通常我们为设备配置动力,总是希望能通过努力去达到“所供即所需”的境界。而“A点转矩”则是58%幅度的电压、额定转速所对应的转矩,它只有全额转矩的3分之1 ,这3分之1的转矩是不能满足负荷需求的!只能靠全额电压所对应的“B点转矩”才能满足负荷的需求!
如果你刘老师只用58%幅度的电压来启动为设备合理配置的电动机,就根本不能把设备的转速拖到“额定转速”,因为58%幅度的电压对应的曲线就是33%转矩曲线,该曲线上对应“额定转速”的点就是“A点”。我们通过对比已经明确知道“A点”的转矩只有“额定转矩”的33%,离设计的负荷需求还远着呢!同时,负荷总是要产生一个“反抗转矩”与“动力转矩”相抗衡,即电机的转矩大小总是跟负荷反抗转矩大小相同的,若负荷在“稳定工作区”需求的转矩,动力达不到,则动力就不可能把设备拖到“稳定工作区”!
引用 刘志斌 的:
3、……同一个负载,怎么出现两个转矩?全压启动后的负载转矩大于降压启动后的负载转矩2倍?
刘志斌看不懂别人表达的意思,我就改进一下:用刘志斌自己画的“机械特性”曲线来作依据吧!
下图由刘志斌在88楼讲解电机星形启动过程时所依据的电机“机械特性”曲线经旋转坐标而得的“转矩-转速”函数曲线
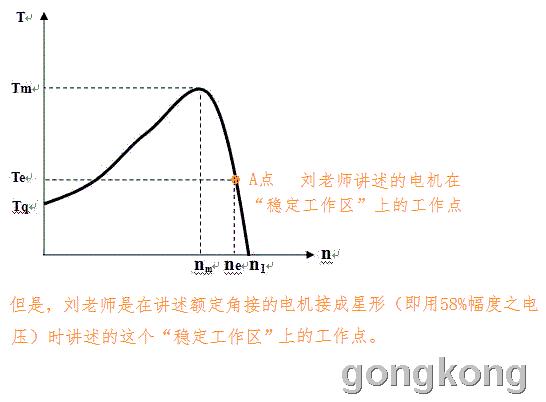
刘志斌在讲解电机星形启动过程时说:
4、楼主的错误在于不了解异步电机的机械特性曲线,不了解异步电机启动时,电机一定要经过最大转矩,就是这个最大转矩把负载拖动到额定稳定运行区的;
其实是刘志斌不了解他自己是用58%幅度之电压下对应的“最大转矩”,也不了解他自己贴的曲线在额定电压、额定转速上对应的工作点B之转矩数值是大于他具体所指的“最大转矩”的!更谈不上了解 冲床、剪板机之类设备在配置动力上的原则!
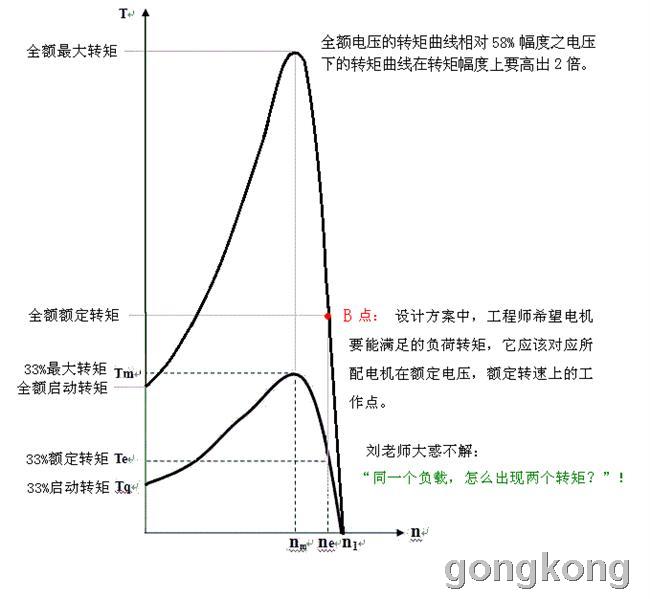
以刘志斌依据的星接降压对应的33%幅度的转矩曲线为基准,其角接全压对应的转矩为前者的3倍!
把100%额定电压下的“转矩-转速”曲线与33%幅度电压下的“转矩-转速”曲线放在同一个坐标系里是为了便于网友们比较星接和角接两个阶段各自对应的曲线上那一部分:
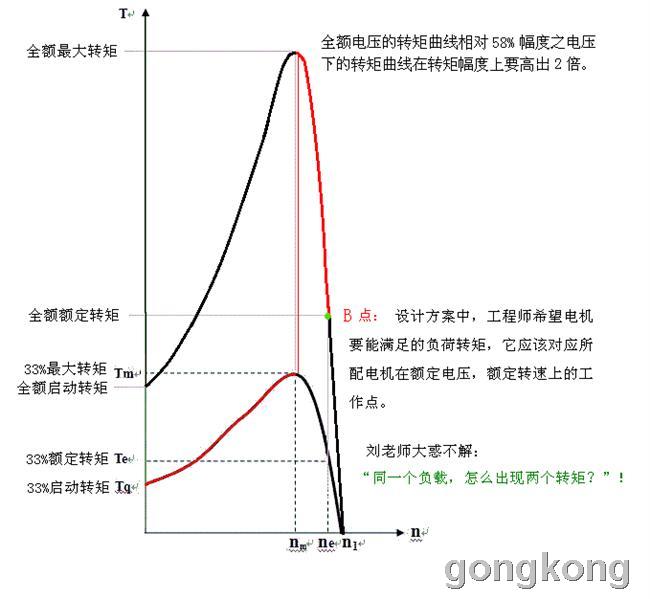
我是认为:同一个转差率的前提下,负载对“动力转矩”呈现出来的“反抗力矩”只有一个数值,这个数值与“动力转矩”大小相等、符号相反(转动方向相反)。当电机绕组上施加的电压由58%幅度切换到100%幅度时,函数f(n)“动力转矩”就在同一自变量(n)的前提下提高到原函数值的3倍!
突然增高的动力转矩使飞轮产生了更高的“角加速度dω/dt”,与此同时,这一增高的角加速度随即产生动态的“反抗转矩”与“动力转矩”的增高部分相抗衡。
这个图并不可能使有真学问的人产生象“同一个负载,怎么出现两个转矩?”这样低级的疑问!
曾经有一位“永动机”发烧网友因其工作是在一家液压动力机械公司担任产品设计,他看到液压马达的功率是跟液压油流量与压强的乘积成正比的;又看到液压泵压出的液压油压强在增压器作用下能够提高很多倍。于是惊喜地声称:他发明了用小功率的液压泵加配增压器来取代大功率液压泵去满足大功率的液压马达-发电机组持续对外输送大功率电能的方法。且经过他的艰苦卓绝的努力,完成了原理性的设计,还申请了中国发明专利!
现在又有人声称:他能用 1/3 “动力转矩”对应的功率,去完成原本需全额“动力转矩”对应的功率才能满足的负荷对动力功率之需求!这不是无异于他在向我们声称:他能推翻《物理学》的“功-能原理”吗?!
关于冲床、剪板机之类的设备上配置动力之原则的有关知识,可以参考我曾经写给“永动机”发烧网友的一篇稿子:《功率不可能持续地被放大》
在现实中,我们虽然可以看到一些“功率”被“放大”的例子,譬如照相机的闪光灯:闪光灯电路用一两节5#干电池,以几伏特的电压,十几毫安的电流来工作,最终要以上千瓦的功率放出非常强烈的闪光;公共厕所自动冲水箱:水箱的输入是一滴滴的小水滴,当水滴满一水箱时,水箱就会以输入时的几千倍的流量输出这一箱水;再如拉弓射箭也是“功率”被“放大”的例子:箭在弦被放开的一瞬间被弹力推动的“功率”可以是弓箭手用力拉开硬弓时的平均功率的上千倍!
但是,等等这些例子并不表明“功”可以被“放大”或“能量”可以被“创生”。这些例子无一不是采用“储能”的装置将在较长时间内以较小的功率把能量积蓄起来达到一定的量值,再在极短的时间内猛的一下子把能量放出来,从而达到“放大”输出“功率”的目的的。在闪光灯的例子中用了“高压电容器的电容”来储能;在冲水箱的例子中用了“水箱的容量”来储能;在射箭的例子中用了“硬弓的形变”来储能。所有这些储能装置都根本不可能放出比其积蓄量值还要多的能量。
冲床、剪板机、腭式破碎机(俗称咬石机)这一类机器的负荷应力具有陡峭的脉动性。当脉冲负荷的巨大应力作用于它们时,需要机器有很大的“功率”,但是,这短暂的脉冲的应力一过,机器所需的“功率”相对就要小很多。所以,我们完全可以不以脉动时所需的最大“功率”给机器设备配置动力,而是以较之小得多的“功率”来配备。为了使机器在受到脉冲应力时有足够的“功率”输出,不致使机器有较明显的速度降低,故而这些机器都无一例外的要配上一个“转动惯量”很大的“飞轮”。这“飞轮”就是一个机械的“储能”装置,它的特性就是其“转速不能突变”。利用这一特性可以平缓脉动负荷对机器转速的影响。但是,这并不是说采用了这种方法就可以随便地以“小”代“大” ,而是要遵守一定的原则,即机器动力的“额定功率”不可小于机器负荷的“平均功率”;也并不是说采用了这种方法就可以只用“较少的能量”来做“较多的功”它同样要遵循“能量守恒”的规律。
由于我们为机器配置的动力的“额定功率”较脉动负荷即时所需功率小很多,所以,当机器受到负荷的脉冲应力时,机器动力所提供的“功率”就肯定不能满足负荷的需求,这时势必引起转速下降,由于飞轮的“动量矩Iω”( I是飞轮的“转动惯量” ω是飞轮的“角速度”)的I很大,ω的微小变化就会使飞轮释放出相当可观的能量,(也可以这样理解:飞轮的转动动能 Wk=1/2 Iω^2 在量值上发生了变化),由于这一变化量是在极短暂的时间内发生的,所以飞轮释放这个能量的功率就相当可观,这个增加的 “功率”叠加在动力的“功率”上使机器在这一短暂时间内有巨大的“功率”输出。从而平缓了脉冲负荷对机器转速的影响。
全武先生说他的“液压增压能动力发电机”是结合了现代科技设计出来的。那么,他的这一(永动机)系统能否将“功率”持续地“放大”呢?
其实,全武说的现代科技就是利用液压原理把增压器高压油缸的压强相比低压缸成很多倍的提高。这一点并不是什么高科技含量的技术,只要机械制造水平能使高压缸达到可承受多高的压强,现有的技术就能轻而易举地办到把液压油的压强提高到油缸所能承受的极限!它的原理非常的简单。我们用手指头把图钉摁入木板就是这个原理,我们的手指头摁压在图钉盖上的力的大小就是图钉挤压进木板的力的大小,作用在我们手指头上的应力所产生的压强很小,对手指皮肤没有一丁点儿的危害,但是同样大的力在图钉针尖上产生的压强却是手指所受到的压强的几十万倍!所以,相对手指皮肤强度要高很多倍的木板也能被这一强大的压强所征服。
压强等于“作用力”与“垂直于作用力的受力面积”之比。图钉针尖上的面积只是图钉盖面积的几十万分之一,所以,图钉把图钉盖上的压强放大了几十万倍作用在图钉针尖上,这有什么可希奇的。液压增压器的低压缸活塞和高压缸活塞是连成一体的,垂直施加在低压缸活塞端面的力会以相同大小和同一方向传递给高压缸活塞,高压缸活塞的端面积如果是低压缸活塞端面积的15分之1 ,那么,在不考虑活塞与缸壁间的摩擦,也不考虑活塞的加速度的条件下,增压器就会把低压缸的压强放大15倍作用在高压缸。(“15 倍”这个数值是根据全武提供的大小活塞的直径“280cm”和“72cm”这两个数据计算得来的)。
在不考虑活塞与缸壁间的泄漏情况的条件下(即理想条件下),进出油缸的液压油的流量等于液压容积在单位时间内的变化量,即等于活塞端面积与活塞运动速度的乘积。由于液压增压器的高/低压活塞是连成一体的,所以,高压缸活塞的运动速度就是低压缸活塞的运动速度。故,在同一时间内,低/高压缸容积的变化量之比就等于它们的活塞端面积之比。即:进入低压缸的液压油流量与高压缸排出的液压油流量之比等于低压缸活塞直径的平方与高压缸活塞直径的平方之比。在全武的例子中,这个比的数值如下:
(280×280)/(72×72)=15.123 (取整数值:15 )
液压功率(KW)=流量(L/min)×压强(Mpa)/60(s/min)
注:这里的分母“60(s/min)”是用于把每分钟流量换算成每秒流量。流量的“升”是“立方米”的“10”的负3次幂,压强的“兆帕”是“帕斯卡”的“10”的6次方幂,功率的“千瓦”是“瓦特”的3次方幂。所以流量“升每秒”与压强“兆帕”(兆牛每平方米)的乘积正好是“千瓦”(千焦每秒)。
- 异步电机降压启动,全压切换时...
 [5996]
[5996] - S7-200仿真软件V3.0汉化版
 [10370]
[10370] - 我的高级技师职业资格**终于...
 [5325]
[5325] - 三菱PLC配方程序怎么写
 [2354]
[2354] - 电气自动化专业英语教材
 [2340]
[2340] - (擂台2周年献礼)单相马达解剖...
 [3412]
[3412] - 我昨天用siemens plc 做的一...
 [4322]
[4322] - 编码器的作用?减速机和变频器...
 [5795]
[5795] - PLC 逻辑表达式?
 [2406]
[2406] - proface触摸屏错误代码RHAA0...
 [5252]
[5252]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号


















 工控网智造工程师好文精选
工控网智造工程师好文精选
