为了当干货，本文不浪费篇幅阐述FFT的原理和算法，这些信息非常多，我们假定客户们已经知晓，有了一些基础。不过说实话，工程师并不一定需要懂原理和会算法，我们大概知道它的意思就行，毕竟会用才是最关键的。

我们先提炼出几个重要的问题点，一般的工程师们只要了解这几点就够用了。

问题1：我们可以用示波器看到某个信号的时域波形，为什么还要用FFT看这个信号的频域波形？

答案是，现实中很多信号的波形看起来长得很复杂，用数学描述它极其困难，甚至人直观的描述它都做不到，那就更谈不上分析它和处理它了。这时候，我们只能换一个思路和方法，在频域上拆解它，就更容易分析处理了。

举个例子：

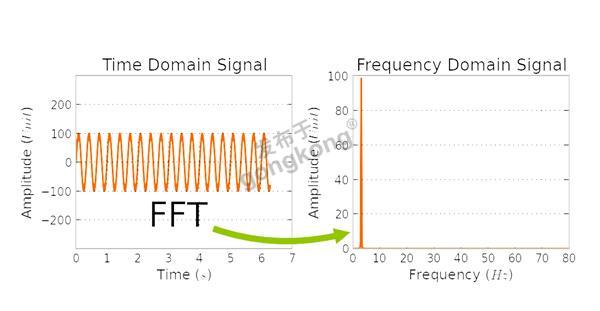
上面这张图，左侧是时域波形，右侧是它的频域FFT波形。从时域波形来看，很简单，就是一个幅值100，频率3赫兹的正弦波。这种情况下，根本没有必要做FFT变换看频域波形。任何关于这个信号的描述和表达都很清晰明了，有明确而简单的数学公式来表示这个信号，要对这个信号做任何分析和处理都有一大堆经典公式和大量的经验方法。

那么来看下面这个图：

现实中，你可能遇到的是这样的一个信号，这是它的时域波形，时域波形也就是时间领域波形的意思，就是横坐标是时间的推移，跟我们的现实直觉认知相符合。那么对面这样一个时域波形，谁能描述清楚它的特征，用简单的数学公式近似表述它，怎么分析和处理它？

这时候就要用到FFT的频域分析，经过分析，我们可以知道，其实它就是三个正弦波叠加而成的：

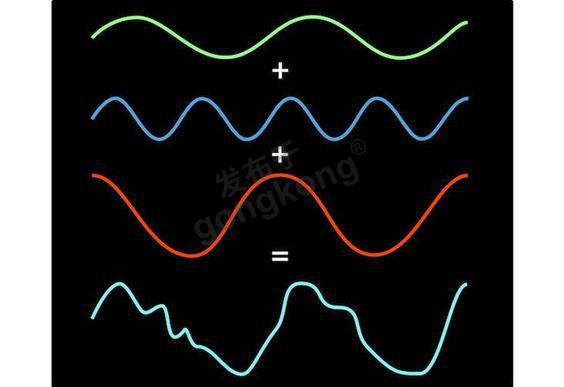
这样我们就能简单准确的表述，分析和处理这个信号。

再看一个类似的例子：

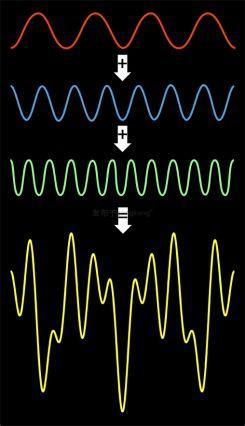
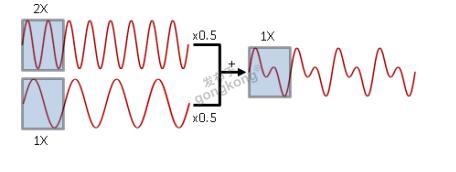
问题2：用FFT做频谱分析具有普适性吗？什么样的信号才能用FFT分析？

答案是肯定的，工程上，我们可以对你采集显示的任何波形进行FFT分析。

通过上面的例子，可能有人会有疑问，虽然上面看到复杂的波形其实是由三个标准的正弦波叠加起来产生的，这是不是故意找的特例？现实中的波形大部分不是这样由三个标准正弦波叠加出来的怎么办呢？

是的，上面的例子的确是找的特例，虽然是特例，但是能很直观的说明问题。那么现实中其他的随机的复杂波形怎么办？没关系，FFT厉害的地方就在这里，理论上，任意波形都可以通过FFT拆解成一系列幅值频率相位不同的标准正弦波叠加而成。

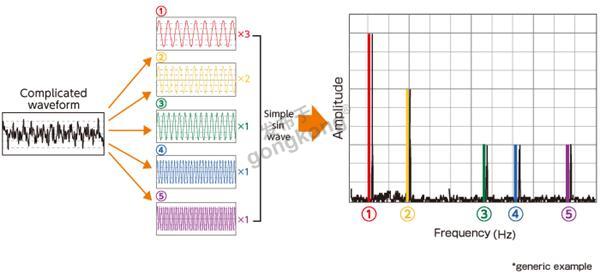
这就类似于一束白光，其实可以拆解成频率不同的色光叠加而成的。时域信号就是那束白光，棱镜就是FFT，拆解出来的不同颜色的光，就是频域波形的不同频率点上的谱线。

我们用LOTO虚拟USB示波器的OSCA02为例，先测一个标准正弦波的FFT频谱，将时域波形与它对应的频域波形对比看看。

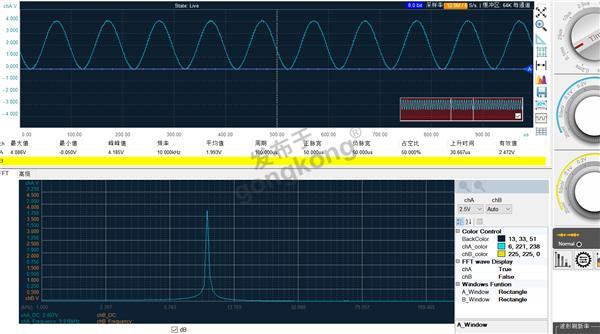
可以看出，一个标准的正弦波，它的FFT频谱就是在对应的频率上的一个高度为正弦波幅值的竖线。

然后我们再测一下一个方波信号对应的FFT频谱的波形：

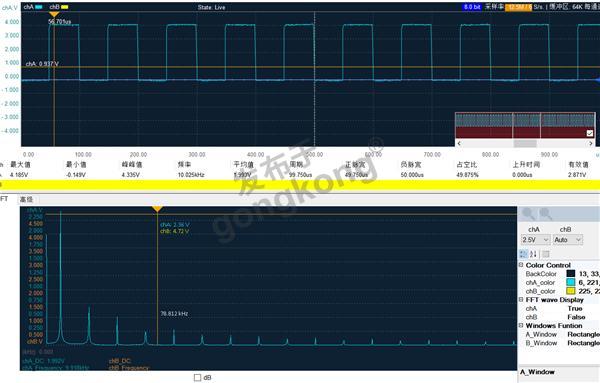
可以看出方波信号可以拆解成一系列正弦波的叠加，这些正弦波就是频谱波形上的那些小竖线。频率与方波频率相同的正弦波分量我们一般称为基波，频率为3倍的正弦波分量称为3次谐波，然后5次，7次谐波等等一直到无限。

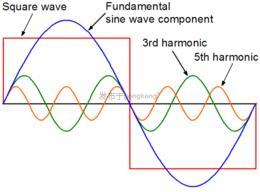
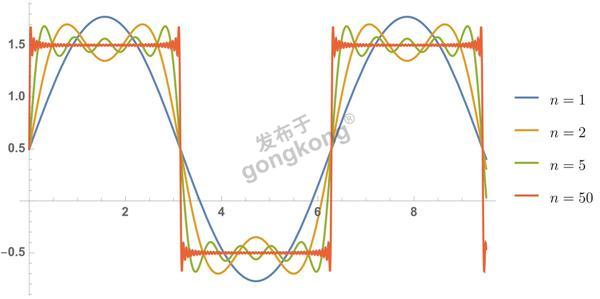
理论上，这个方波是由无限个正弦波分量叠加而成的。工程上，我们其实不需要去处理无限多个分量，因为这样工作量太大且没有必要，一般只是取前多少个分量进行分析处理就可以近似达成目标了。下图所示，一个方波，取前多少个正弦波分量叠加以后变成的不同的方波。可以看到，取的分量数（n）越多越接近原始方波，其他现实波形的道理是一样的。

关于LOTO示波器使用FFT功能的视频演示如下：

https://www.bilibili.com/video/BV11k4y1z7KA

问题3：FFT频谱分析有什么用？

典型的应用场景有很多。

比如说，当你的信号上被噪声干扰了，你想去掉这个噪声。在时域波形上看，只能看出是一个密集的上蹿下跳的噪声，完全看不出其他有助于解决掉噪声的信息。这时候用FFT分析，可以得知噪声分布的频率范围，可以针对一些主要的噪声频点进行有针对性的滤波处理。

再比如，音频应用中，通过人耳朵很难客观和标准化分辨出来一些音频处理单元的频率范围。使用FFT对音频处理单元的信号进行扫频和分析，可以定量的得出音频响应的频谱范围，从而快速确定音频单元是否合格。

关于FFT使用时候的误差与频谱泄漏：

工程中最容易出现的FFT误差，是由于参与FFT计算的采样点数相对于这些采样点数覆盖的信号信息量太少了。举个简化的例子

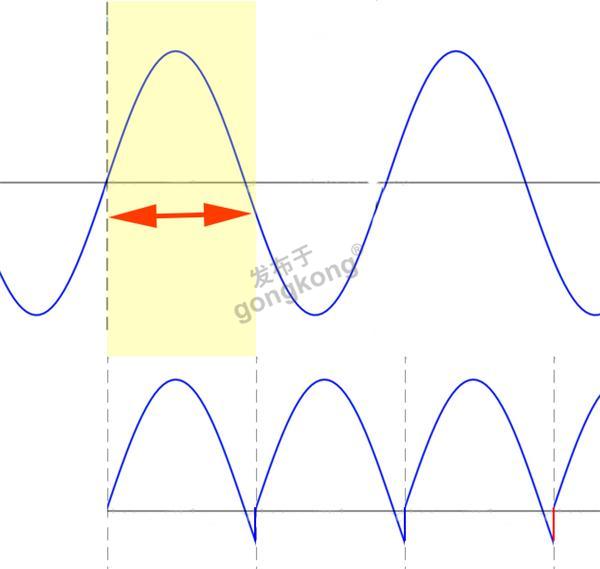
上图中的假如一个正弦波（上方）被采集到，如果在做FFT分析的时候由于参与FFT点数的设置，可能只取了黄色区域的局部波形数据进行FFT计算。那么在FFT算法看来，它会认为FFT针对的信号是黄色部分的周期性延宕，如图中下方的波形所示。

显而易见，这样进行FFT计算得出的结果肯定是错误的。而且可以推理，使用的FFT点数越少，错误越严重。

我们实测一下来看：

还有一种情况是，上面提到的FFT取点数的时候，点数足够大，但是并没有取到刚好整周期上，稍微偏差一点，这样进行FFT分析并不会产生错误，但是会有些误差，这些误差正是由于这些小偏差引起的，这是难以避免的，专业术语叫做频谱泄漏，如下图所示。

在频谱泄漏在频谱上的表现为在正确的主频谱旁边出现不该出现的短小的频谱。

我们用USB虚拟示波器实测一下频谱泄漏：

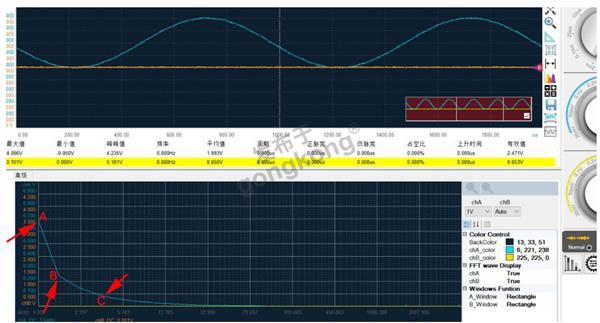
上图是实测的1K频率的正弦波的时域波形和FFT幅频曲线。理论上，FFT曲线应该是在1K频率分量上的一根竖线，如A点所示，但是实际FFT结果并不是理想的在A处的一根竖直线，而会在临近的B点和C点还有一定的频谱值。B和C点不陡降到0是频率泄漏导致的。

解决频谱泄漏的最常见的方法是加窗函数：

我们一般默认用的是矩形窗，不同的窗函数能不同程度的改善谱线的圆润程度。以上面的频谱泄漏图为例，由于突然截断造成周期延拓时两个周期相邻处出现了信号突变，这种突变，代表的是信号包含了高次谐波。加上合适的窗函数，可以把这个突变变得圆滑一些，从而抑制高次谐波。

但是，我们也可以这样想，频谱泄漏图中的下方信号就是真实信号，那么，加上这样的窗函数反而得到了错误的结果。

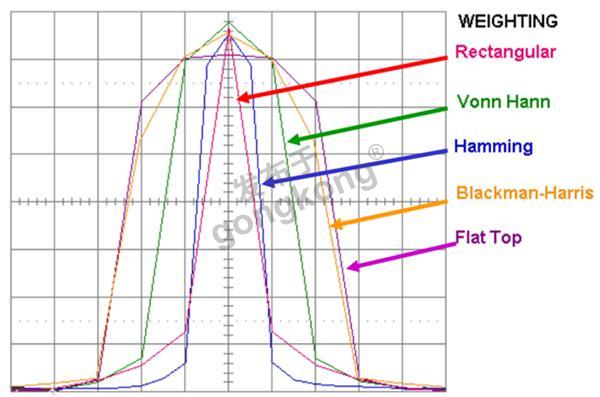
上图为不同窗函数的圆润效果，坦白讲，一般是不太用窗函数的，除非非常了解自己的应用情况，使用窗函数的时候计算负担比较重也是我不太常用它们的原因之一。