也来谈谈传递函数的问题 点击:6854 | 回复:114
也来谈谈传递函数的问题
1、传递函数是针对一个确定对象而言的;
2、这个对象的输出量与输入量的比值叫做这个研究对象的传递函数;
3、这么一说,大家会明白很多,这不就是一个放大器的放大倍数吗?你说对了,对于一个电压放大器,输出的电压与输入的电压之比,就是电压放大倍数,它就是放大器的传递函数;
4、知道研究对象的传递函数有什么作用呢?
1)例如一个共射电压放大器的直流电压放大倍数=βRc/rbe;
2)有了这个电压放大倍数,我们可以清楚的知道怎样提高电压放大倍数,选用β高、增大Rc、减小rce;
3)这个电压放大倍数的公式,一般不是真用它来计算放大倍数的,而是有了它我们知道怎样设计、调试一个放大器;
4)如果谁想知道一个对象的传递函数,从此把它当做一个公式、方程来用,就想偏了!
楼主最近还看过
21、为什么伺服电机的传递函数与一般电机的传递函数不同,这就是伺服电机与一般电机的最大区别:
1)一般电机就是一个把电能转换成机械能的装置;(伺服电机不是,几十千瓦的伺服电机是用来做信号处理的。我见过日本本土制造的分切机,可以用来分切纸张和薄膜,运行速度可以达到300MPM,1000英尺的分切长度,设定和实际长度相差不到1英尺。但是那么重的纸卷(超过500公斤)是靠信号处理机处理的!)
2)而伺服主要完成的是,根据输入的信息电流脉冲完成给定的角位移;(小菜了,谁叫咱只有这个本事!)
3)如果把普通调速电机套上编码器用上位机输入的指令脉冲与反馈脉冲比较、做成开关式电机自动控制装置称作伺服,是概念性错误! (很常见了,见没有见过普通电机,采用伺服控制器控制的?没有人对叫不叫伺服感兴趣,但是工作原理的理解不会有任何问题!)
4)伺服脉冲式步进控制,是伺服精确控制的必由之路,没有捷径可走;(谁叫咱天生只会这么走路呢,可是咱走快了那姿态优美的你根本认不出咱是谁生的,但是咱有一项本事起步快,刹车急。别的就不行了)
5)编码器的使用只是检测反馈的精度提高了,而电机、工件的位移的精确控制就成为伺服控制的瓶颈!(什么东西没有瓶颈呢,咱不在乎?低低的问一句,传递函数呢?)
1、前边说的那些传递函数,都是开环传递函数,有些研究对象的输出对输入有反馈,这样研究对象就处于一个闭环工作状态; (前面讨论了哪些传递函数,我没有看到一个可以算传递函数,因为物理过程我没有见到微分方程,拉氏变换也没有清晰表示出来,传递函数没有什么开环闭环,只有系统才有。)
2、闭环传递函数的定义与开环传递函数的意义相同,但是闭环时,由于输出对输入的反馈,使的传递函数的关系式复杂了很多,特别是增加了微分项,很多情况下,求解传递函数的过程变为求一个微分方程的解;(微分项是不存在的,微分环节一般也不是由反馈增加,这要看系统本身。怎么求解传递函数,反而要通过求解微分方程来做?这不是本末倒置吗?)
3、这样大家习惯于用拉氏定理,来求解传递函数的微分方程,很方便! (荒谬!!!)
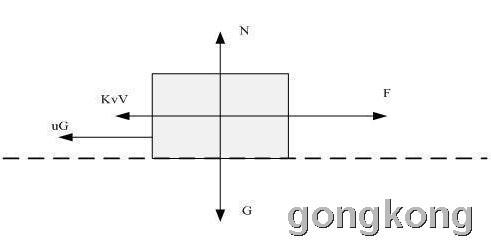
水平运动体M的受力分析
我们来看一看,刘老师这张图片:
根据牛顿第二定律
f(t) -K1*v-K2*m*g=m*dv/dt
这里K1=Kv,K2=u,在不容易混淆的情况再还原回去。
f(t)=K1*v+K2*m*g+m*dv/dt,这个式子由于含有K2*m*g 这一项,它与v(t)无关,所以直接进行拉氏变换,不能直接求出传递函数。所以假设K2=u=0,则两边进行拉氏变换。F(s)=(K1+m*s)V(s),如果一F(s)作为输入,V(s)作为输出。则传递函数V(s)/F(s)=1/(K1+m*s),这是什么?这是一阶系统的传递函数,m/K1代表一个时间常数,他与时域分析里边一个指数衰减时间按常数是同一个量。
所以刘老师的传递函数框图是错的,这是一个开环的一阶系统!
4、忽略水平摩擦力、空气阻力,求水平运动体的开环传递函数:
1)输出速度函数: v(t) = (F/M) t =(1/M) t (F = 20.6N -19.8N =1N)(错!输入激励f(t)与速度v(t)的关系是一阶微分方程,数值解法也不是这么做的!)
2)输出速度函数v(t) 的拉氏变换:V(s) = (1/M) /s^2 (表序号4) (错!前面已经解出了)
3)输入力F(t)函数:F(t) = 20.6N-19.8N =1N (这是求值还是求函数呀!)
4)输入力F(t)函数的拉氏变换:F(s) = 1/s (表序号3) (无言)
5)拉氏变换下的开环传输函数如下:
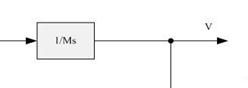
V(s) /F(s) = 【(1/M) /s^2 】 / (1/s ) = 1/Ms (错!)
5、拉氏变换下的闭环传输函数G(s)(忽略摩擦力):
1)已知反馈系数为Kv=0.1,开环增益为1/Ms,
2)则闭环传输函数G(s)为:
G(s) = (1/Ms) / 【1+(1/Ms)Kv】 = (1/Kv) / 【1+(Ms)/Kv】
6、用拉氏传输函数计算运动体的运动参数:
1)将 Kv = 0.1、M = 10Kg 、u=0.2、uMg = 19.6N 、F = 20.6N 代入传输函数:
G(s) = (1/Kv) / 【1+(Ms)/Kv】 = 10 / (1+100s)
2)求稳定输出速度、加速时间:
3)输入拉氏函数F(s):
a.力函数 F(t) = 20.6-19.6 = 1N;
b.输入拉氏函数F(s)为:F(s) = 1/s;
4)通过传输函数G(s)求输出速度函数V(t):
V(t) = L^(-1 )【G(s) ×F(s) 】
= L^(-1 )【10 / (1+100s) × 1/s 】
=L^(-1 ){10×【1/s(1+100s)】 }
= L^(-1 ){10×【0.01/s(0.01+s)】 }
= 10×(1 - e^-0.01t) (表序号9)
5)由输出速度函数 V(t) = 10×(1 - e^-0.01t) 讨论:
a.当e^-0.01t→0时,
V(t)有最大值= 10(m/s);
b.e^-0.01t→0 ,
e^0.01t→∞,t →∞,V(t)有最大值= 10(m/s);
c.若 t = 100秒时,
V(t) = 10 × (1 - e^-1) =10 × (1 - 1/2.7)
=17/2.7
=6.3(m/s)
d.若 t = 200秒时,
V(t) = 10 × (1 - e^-2)
=10 × (1 - 1/7.3)
=63/7.3=8.6(m/s)
e.若 t = 0秒时,
V(0) = 10 × (1 - e^0)
=10 × (1 - 1)
= 0(m/s)
工程控制论创始人钱学森如此定义传递函数:
“我们已经看到,在用拉氏变换法处理问题的时刻,常系数线性系统的运动状态和多项式D(s)有着本质的联系。D(s)...的系数也就是微分方程的系数。不仅如此,就是在一般的情形里,如果初值问题里的y(t)的初始值和各项初始导数值都是等于零,那么,那么系统的运动状态也是由两个多项式的比值N(s)/D(s)所完全确定的。我们是用F(s)表示这个比值的。如果驱动函数的拉氏变换是X(s)而特解的拉氏变换是Yi(s)的话,...就给出
YI(s)=F(s)*X(s)
可以把这个方程看作一个运算子方程;X(s)受到运算子F(s)之后就变成了Yi(s),或者说F(s)把X(s)变成Yi(s)。因此我们就把函数F(s)称为系统的传递函数。”(上面话完全是钱学森本人所讲,是从《工程控制论》中文版摘录)
刘老师这么看:那么是不是拉氏函数表示的传递函数才是传递函数呢?显然不是,在传递函数的定义里,没有规定传递函数必须是拉氏函数;
钱老已经说的如此明白,还需要争论吗?
当然许多教科书不像钱老这么直率,搞的一帮学子昏昏然,才莫名其妙的发明很多新的说法。我们一用伽利略的口气。“也许我是错的,可是我就是靠他把卫星送上天的呀!”(仿钱学森语录)
4、我在18楼用初等函数表示伺服转子惯性体J的传递函数为传递函数2=S/J; (S是什么,是微分环节的s吗?,如果是惯性环节怎么会是微分环节呢?如果不是,是什么?J到底是指惯性体,还是转动惯量!)
5、我在2楼用初等函数表示“水平面内的运动体,质量为M,水平作用力为F,水平速度为V”惯性体M的传递函数=S/M; (怎么还是微分环节吗?可是刚刚明明好象是积分环节或一阶环节?)
6、传递函数中的S是时间,单位是秒,表示力F的作用时间;(这一定是独创,量纲分析也不会导致这么一个东西呀!在传统概念里,连理解成频率都胆颤心惊,只有在转换到复平面上进行频域分析的时候才敢当作某种频率来看,现在怎么变成时间量了呢?看来还有一个时域分析用的传递函数,要不传递函数怎么会有微分方程形式呢?别信我的,我瞎说的!)
7、如果用拉氏传递函数,则分别为“1/Ms”、"1/Js",1/s是力F的作用时间,你现在可以看到,用初等方法得到的传递函数与用高等拉氏变换得出的传递函数实质是一么一样的!(如果s是时间量,1/s就不可能是时间量,怎么成了作用时间了!没有初等方法的拉氏变换!初等方法也不会有传递函数!)
8、但是用初等函数表示的传递函数的物理意义很明确,大家都可以理解,而那个拉氏传递函数的物理意义一般人不理解,这就是我在3楼描述的结论; (从上面反驳即知道其荒谬了)
10、其实有一种情况:
1)在一个运动系统中,由许许多多个个体对象构成的环节组成,这时我们必须求出各个环节中对象的传递函数,然后把他们乘起来,就是运动系统的传递函数;(见二楼)
2)注意,在这个计算过程中得出的各个环节的对象的传输函数,不能有的是初等函数,有的是拉氏函数; (乱弹!初等函数是初等函数,拉氏变换是拉氏变换,是在谈不同的东西,没有什么拉氏函数!天呀!)
3)注意,在这个计算过程中得出的各个环节的对象的传输函数,要么都是初等函数,要么都是拉氏函数;(同上,乱弹!)
- 【今日看点】带你见识下什么是...
 [1245]
[1245] - 台达变频器C2000检测到IGBT温...
 [2253]
[2253] - 川崎机器人仿真软件求助
 [835]
[835] - 美国AB公司PLC折弯机程序.有...
 [785]
[785] - 焊接机器人编程
 [370]
[370] - 他励直流电动机空载运行的电...
 [1363]
[1363] - 寻混凝土固废处理方案
 [611]
[611] - 个人接了一个活想请教大家
 [2351]
[2351] - 为什么PLC上电后,程序不运行...
 [841]
[841] - 组态王 反应慢
 [1415]
[1415]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号


















 工控网智造工程师好文精选
工控网智造工程师好文精选
