也来谈谈传递函数的问题 点击:6854 | 回复:114
也来谈谈传递函数的问题
1、传递函数是针对一个确定对象而言的;
2、这个对象的输出量与输入量的比值叫做这个研究对象的传递函数;
3、这么一说,大家会明白很多,这不就是一个放大器的放大倍数吗?你说对了,对于一个电压放大器,输出的电压与输入的电压之比,就是电压放大倍数,它就是放大器的传递函数;
4、知道研究对象的传递函数有什么作用呢?
1)例如一个共射电压放大器的直流电压放大倍数=βRc/rbe;
2)有了这个电压放大倍数,我们可以清楚的知道怎样提高电压放大倍数,选用β高、增大Rc、减小rce;
3)这个电压放大倍数的公式,一般不是真用它来计算放大倍数的,而是有了它我们知道怎样设计、调试一个放大器;
4)如果谁想知道一个对象的传递函数,从此把它当做一个公式、方程来用,就想偏了!
楼主最近还看过
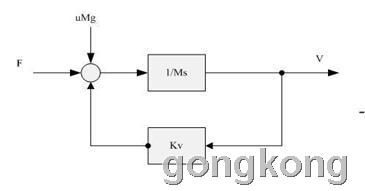
6、用拉氏传输函数计算运动体的运动参数:
1)将 Kv = 0.1、M = 10Kg 、u=0.2、uMg = 19.6N 、F = 20.6N 代入传输函数:
G(s) = (1/Kv) / 【1+(Ms)/Kv】 = 10 / (1+100s)
2)求稳定输出速度、加速时间:
3)输入拉氏函数F(s):
a.力函数 F(t) = 20.6-19.6 = 1N;
b.输入拉氏函数F(s)为:F(s) = 1/s;
4)通过传输函数G(s)求输出速度函数V(t):
V(t) = L^(-1 )【G(s) ×F(s) 】
= L^(-1 )【10 / (1+100s) × 1/s 】
=L^(-1 ){10×【1/s(1+100s)】 }
= L^(-1 ){10×【0.01/s(0.01+s)】 }
= 10×(1 - e^-0.01t) (表序号9)
5)由输出速度函数 V(t) = 10×(1 - e^-0.01t) 讨论:
a.当e^-0.01t→0时,
V(t)有最大值= 10(m/s);
b.e^-0.01t→0 ,
e^0.01t→∞,t →∞,V(t)有最大值= 10(m/s);
c.若 t = 100秒时,
V(t) = 10 × (1 - e^-1) =10 × (1 - 1/2.7)
=17/2.7
=6.3(m/s)
d.若 t = 200秒时,
V(t) = 10 × (1 - e^-2)
=10 × (1 - 1/7.3)
=63/7.3=8.6(m/s)
e.若 t = 0秒时,
V(0) = 10 × (1 - e^0)
=10 × (1 - 1)
= 0(m/s)
也来谈谈传递函数的问题
1、传递函数是针对一个确定对象而言的;(得看怎么定义对象,假如我看中一个女孩,我向她看过去,那女孩也恰恰注意到了我。她脸红了。好了这里肯定有一个什么函数。为什么呢?应为我的目光,经过一个延时,变成了她的脸红。至于脸红表示什么,咱不知道。突然一个男孩也在看她,不小心撞到电线杆上,她花容失色,惊叫起来,把我吓了一跳。你说这个情节中怎样定义对象?楼主这句话虽然从常识来讲也没有什么问题,问题在于我们讨论问题,只在于圈定一个条件,确定一个边界,讨论这个边界里面的东西,这个叫系统。而不会理会是不是确定和是不是对象!)
2、这个对象的输出量与输入量的比值叫做这个研究对象的传递函数;(这个定义是错的。传递函数是系统输出(响应)和输入(激励)的某一个比值。但是有两个条件:(1)系统输入(激励)的初值为零;(2)传递函数一定是输出变量的拉氏变换和输入变量的拉氏变换的比值。直接用函数比不行,采用傅立叶变换也不行)
3、这么一说,大家会明白很多,这不就是一个放大器的放大倍数吗?你说对了,对于一个电压放大器,输出的电压与输入的电压之比,就是电压放大倍数,它就是放大器的传递函数;(只有当放大器只是含有一个比例环节时,上述讲法才正确,如果放大器输入带有滤波电容,虽然放大倍数一样,但是传递函数就不一样了。)
4、知道研究对象的传递函数有什么作用呢?(有用肯定有用,但是不是这里可以讨论清楚的,我的三不主义,就是觉得擂主这个题目有点。。。。。。)
1)例如一个共射电压放大器的直流电压放大倍数=βRc/rbe;
2)有了这个电压放大倍数,我们可以清楚的知道怎样提高电压放大倍数,选用β高、增大Rc、减小rce;
3)这个电压放大倍数的公式,一般不是真用它来计算放大倍数的,而是有了它我们知道怎样设计、调试一个放大器;
4)如果谁想知道一个对象的传递函数,从此把它当做一个公式、方程来用,就想偏了!
5、现在说的传递函数,是广义上的传递环数;(可以研究,但是和我们工作真没有什么关系)
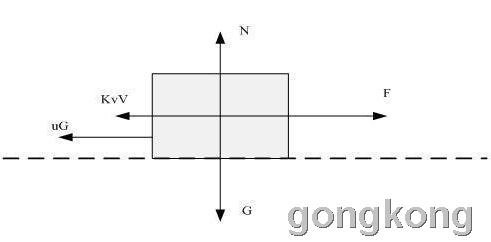
6、例如一个质量为M的物体,在水平面内给一个作用力F,它就会产生一个加速度、速度v,这时候这个物体就是研究对象,它的输入量就是作用力F,输出量就是速度V,输出量速度v与输入量F的比就是这个物体M的传递函数;
含混之极!清晰的表述见下:
f=Md(dv/dt)/dt,F(s)=M*s2V(s),传递函数G(s)=F(s)/V(s)=M*s2,or G1(S)=1/G(s)=1/(M*s2)
7、那么广义上的传递函数,和狭义上的传递函数有什么不同呢?(不知道)
1)例如电压放大倍数,是两个电压的比值,是一个纯数,没有单位名称;(这不一定可以算传递函数呀!)
2)而上边的物体M的传递函数,是两个完全不同性质的物理量的比,这个比值有单位、有名称、有意义;(传递函数本身就有意义啊,所以它有量纲有什么不对呢?但是传递函数本质是将时域分析中的解微分方程,变成复平面上解代数方程,所以这个题目不适合在这里讨论。)
3)而上边的物体M的传递函数是:(以下都不是控制理论讨论的议题,充其量是一些不准确的物理定义式)
传递函数=速度V/作用力F
作用力F×传递函数=速度V
作用力F×(S/M)=速度V
作用力F×S=M×速度V
F×S是力的冲量,M×V是物体的动量的增量,“作用力F×S=M×速度V ” 是冲量定理,那么传递函数=S/M,就是时间S与质量M的比,单位是秒/Kg;
10、由于研究对象不同,传递函数可能是一个简单的数、一个简单的初等函数,也可能是一个微分方程,这个微分方程可能有解,也可能无解;(传递函数根本不可能是微分方程,传递函数本质是将时域分析中的微分表达式,变成复平面上代数表达式,传递函数形式上为两个代数式之比。)
11、如果研究对象的传递函数,是一个微分方程,恰好是一个可以用拉氏定理可以解的微分方程,就是用拉氏变换地方法;(概念含混,再重复一遍:传递函数本质是将时域分析中的微分表达式,变成复平面上代数表达式,)
12、有人不懂其中的道理,认为只有拉氏变换的函数才是传递函数,认为传递函数怎么能是初等函数呢?太可笑了!(这个讲法本身就可笑,只有拉氏变换才有传递函数!拉氏变换本身是线性微分方程变换过来,当然传统概念上传递函数都是初等函数。但是由于非线性系统的应用,有些传递函数不能用代数式表达,这些应用超越式表达,于是不算初等函数。)
好吧!既然刘老师这么讲。我们就来看一看什么叫传递函数以及传递函数的意义。钱学森是国际上公认的工程控制论之父。他在《工程控制论》中论及传递函数时和一般的教科书是不同的,他首先强调传递函数实际工程上的意义。
“我们已经看到,在用拉氏变换法处理问题的时刻,常系数线性系统的运动状态和多项式D(s)有着本质的联系。D(s)...的系数也就是微分方程的系数。不仅如此,就是在一般的情形里,如果初值问题里的y(t)的初始值和各项初始导数值都是等于零,那么,那么系统的运动状态也是由两个多项式的比值N(s)/D(s)所完全确定的。我们是用F(s)表示这个比值的。如果驱动函数的拉氏变换是X(s)而特解的拉氏变换是Yi(s)的话,...就给出
YI(s)=F(s)*X(s)
可以把这个方程看作一个运算子方程;X(s)受到运算子F(s)之后就变成了Yi(s),或者说F(s)把X(s)变成Yi(s)。因此我们就把函数F(s)称为系统的传递函数。”
这是一个大师的描述,没有很好的数学基础可能根本无法理解上面在讲什么,但是如果有好的数学基础,上面的陈述烤熟你传递函数引用的真正目的:是为了方便地描述系统的运动状态。这个定义里面明确有几点与刘老师的传递函数不一样:
1、传递函数是为了方便描述和求解系统运动状态而引入,而不是针对“所谓对象”而引入;
2、传递函数仅解决系统运动的初值为零的状况,它只能求出系统初值为零的一个特解;
3、只有拉氏变换才与传递函数有关,其余变换与传递函数没有关系;
4、在传统意义上传递函数是两个代数式的比值,是一个初等函数。
11、如果研究对象的传递函数,是一个微分方程,恰好是一个可以用拉氏定理可以解的微分方程,就是用拉氏变换地方法;
这里面第一个错误是,传递函数不可能是一个微分方程,第二个错误是也没有什么可以解微分方程的拉氏定理,微分方程用来描述系统状态是时域分析方法,转换成传递函数是在复平面上来求解系统运动状态。这两个是等效的,但是处理传递函数比解微分方程方便。拉氏变换主要目的不是为解微分方程。钱老在论及这个问题时写到“从Y(s)变回y(t)的这个步骤实际上是很少需要的”这就像我们说今天下雨了,在表示的意义方面,用汉语和英语有什么区别呢,从技术角度只是语音编码不同!
12、有人不懂其中的道理,认为只有拉氏变换的函数才是传递函数,认为传递函数怎么能是初等函数呢?太可笑了!
拉氏变换的函数不一定是传递函数,传递函数在线性系统里一定是初等函数,传递函数怎么能是初等函数呢?太可笑了!
14、之所以说是最笨的方法,原因是运动系统的控制的各个环节的物理关系、物理因数是非常明确地,怎么做大家都很明白,用方程式表示出来的传递环数无非是这些物理关系、物理因数的一个无谓的集合;(不知道在讲什么!)
15、但是,要真正写出运动系统的传递函数,确实不是件容易的事,是个十分劳民伤财的事,写出来的结果和直接研究各个环节的结果其实是一样的;(看来还是不明白为什么要引入传递函数,物理学描述物理过程最有用的方法之一是微分方程,微积分的发明人之一牛顿本身就是基于研究万有引力的需要。只要是常系数微分方程可以描述的系统,使用传递函数求解系统状态是最方便的。我们很难想像求解一个高阶微分方程的难度。但是传递函数是分式,利用复变函数论,不必求解方程就可以确定系统各项性能指标。因为直接处理微分方程在工程上是不方便的,科学家们才另想办法,这么一个聪明的想法竟然成为最笨的方法。不要说高阶系统,你求一个二阶系统看看?项数、系数稍微变化一下,就够头疼了。)
16、例如上面说的那个物体M在水平面内的运动,谁都会知道,作力F大、作用时间S长,物体的速度v就会大,一个不识字的农民做工时都知道这个道理;(如果这样,这么简单的道理,还用伽利略、牛顿说,真笨,太阳明明绕着地球转,还要为这么一个简单道理,上绞刑架。笨死了!)
17、而写出的传递函数,特别是用拉氏函数表示时,一个工控网的人都给弄蒙了!(那只能说修行太浅,工控人的基本工具都不会用,看来工控家园改为菜园得了。特别是一些资深人士,记得花瓣女人还是谁的说相砸坛子,好!不愧是女中豪杰!)
- 【今日看点】带你见识下什么是...
 [1245]
[1245] - 台达变频器C2000检测到IGBT温...
 [2253]
[2253] - 川崎机器人仿真软件求助
 [835]
[835] - 美国AB公司PLC折弯机程序.有...
 [785]
[785] - 焊接机器人编程
 [370]
[370] - 他励直流电动机空载运行的电...
 [1363]
[1363] - 寻混凝土固废处理方案
 [611]
[611] - 个人接了一个活想请教大家
 [2351]
[2351] - 为什么PLC上电后,程序不运行...
 [841]
[841] - 组态王 反应慢
 [1415]
[1415]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号


















 工控网智造工程师好文精选
工控网智造工程师好文精选
