了解六西格玛的伙伴们都知道，西格玛前面对应的数字越高，产品或过程合格率也越高，通常见到或听到的x个西格玛对应的缺陷率为：

6个西格玛=3.4ppm 　　

5个西格玛=233ppm 　　

4个西格玛=6,210ppm 　　

3个西格玛=66,810ppm

2个西格玛=308,700ppm 　　

1个西格玛=697700ppm

为什么6个西格玛对应的缺陷率对应的是3.4ppm,而不是其他的呢？

这里所讲的缺陷率就是缺陷机会，即百万分之的缺陷机会（DPMO）。几个六西格玛就是指几个六西格玛水平通常用Z 表示。公式为 Z=|TU - TL|/2σ

通常上下3个西格玛包括了99.7% 的数据；当达到6个西格玛时，在上下限内通常会包含 99.99999982的数据。而这个99.99999982 的数据 即缺陷机会为0.0018ppm和 本文开头提到的数据3.4ppm是不一致的。我们看看下面两组数据：

1）6σ（Sigma=西格玛）=0.0018ppm

2）6σ （6Sigma=西格玛）=3.4ppm

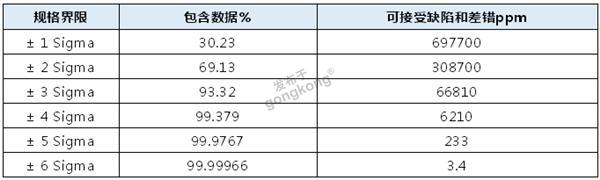
根据上面这两个数据表，我们可以看出通常人们说的六西格玛水平对应缺陷机会是3.4ppm, 而不是第一个数据表对应的0.0018 ppm, 这是为什么呢？

是不是很奇怪？

那么这6个西格玛水平对应的3.4ppm 缺陷机会是哪里来的呢？

在统计学上，达到六西格玛水平时，缺陷机会只有0.0018ppm,而非3.4ppm。在这3.4ppm时，过程缺陷也接近于零，几乎可以忽略不计。但实际上根据本文表一中对应的3.4ppm 缺陷率对应的大致只有4.5个六西格玛水平。这里就产生了1.5 个西格玛的偏差或漂移。其中真正的原因和逻辑是六西格玛在实践中的经验总结：流程在短期内的表现比长期内的实际表现要好，因为在短期内只要处理正常的过程变化，而在长期的过程也会出现特殊的过程变异，这就导致了短期内表现为6个西格玛水平，而长期表现为4.5 个西格玛水平。过程变异的长期变化主要由两个原因构成：

1）过程平均值随时间变化；

2）随着时间推移，该过程的标准差的增大；

在长期过程中由于两者之一或两者结合的影响，导致流程无法达到正真的六西格玛水平。这种变化，也称为长期均值变化。长期均值变化，不符合六西格玛标准，但我们怎么知道从正态曲线的两边各去掉1.5个西格玛水平呢？其实这并不是统计学上的结果，而是长期的行业惯例，大名鼎鼎的摩托罗拉公司是六西格玛方法论的先驱者，其通过大量的例证，同样得出1.5 西格玛偏移的结论。虽然也有人对此提出质疑，但由于摩托罗拉公司榜样的作用，所以行业内也就接受了 6西格玛水平对应 3.4ppm 缺陷机会。

注意，通常计算6σ水平时用到的数据都是长期数据，而不是短期数据，但6σ结果通常是看短期数据结果。