矢量控制：真实 or 谎言 ？ 点击：27601 | 回复：415
孔子曰：“朝闻道，夕死可矣”。
变频器的技术发展很快无数，从最初的V/F控制，到后来的闭环矢量控制，再到开环矢量控制，经历了一个较长的过程。其中开环矢量控制在1980年代由日本安川公司率先得以实现，是一个非常成熟的控制体系。本人做过实验，开环矢量控制，以安川616G5为例，在1Hz的运行频率下，也能达到150%的额定转矩。
我国在自动控制领域与日本或其它发达国家的已经存在巨大差距，如果到现在，我们还停留在讨论“矢量是否是个骗局”这样的一个水平上，无疑将对初学者学习变频器知识会有很大的伤害。所以发表此篇文章，力求深入浅出，方便大家理解矢量的基本含义。如有不对的地方，敬请朋友们提出指正的意见。
“矢”者，箭也。我们知道，要让弓箭发挥作用，力度和方向都要控制好。所谓“矢量”，指的是既有大小又有方向的量。那么，“矢量控制”，也就是对方向和力度同时进行控制。
如何理解矢量控制，我们需要先搞清电机的力的来源。我们一般所指的电机力，都来源于一个基本的原理，就是磁铁同极性的排斥力，或者是异极性的吸引力。在此，可以先把电机的运动简化为2块磁铁之间试图对齐，而我们努力不让它们对齐的结果。
从简单的开始，我们先来看看直流电机。对于直流电机，天生就实现了矢量控制。
1.先看看两块磁铁分别在哪里？定子是一块空间位置固定不变的磁铁（在此，我们只讨论最为常见的他励方式），转子是另一块磁铁。
2.有人会问，一块固定的磁铁，一块旋转的磁铁，磁力线还怎么对齐啊？请看下一条。
3.转子通电即产生磁场，形成另一块磁铁。这个磁铁与定子磁铁的夹角恰好为90度。
4.转子受到磁力的影响产生转动，会偏过一个很小角度，然而此时通过换向器和电刷的配合，转子磁场很快又调整回来了。也就是说，转子虽然在动，转子所形成的的磁场基本没有动。
5.这样，方向的控制，通过电刷、换向器、转子绕组的配合得以实现。
6.此时，只要控制好转子的电流，就控制了力的大小。
接下来，我们再来看看交流电机的情况。
1. 定子通过的是三相交流电，产生的是一个旋转磁场。因此，可以认为定子磁铁是不断旋转的。
2. 要实现矢量控制，首先必须让转子的磁铁也同步地转起来。
3. 电机的电磁转矩与定子磁场强度、转子磁场强度、2块磁铁之间的夹角的正弦成正比。关于这一点不难理解，两块磁铁对齐的时候（0度，sin0°=0;）,不存在电磁转矩；两块磁铁相差90度的时候（sin90°=1;）,电磁转矩达到顶峰；
4. 接下来控制的目标就是：
1）稳定其中的一个旋转磁场的强度（恒定磁场）；
2）控制磁铁之间角度为90度（磁场定向FOC）；
3）控制另一个磁场（受控磁场）的强度以达到控制电磁转矩大小（力矩控制）。
5. 关于坐标变换的物理意义（以同步电机为例）：
1）在电机不失步的情况下，可以认为两个磁极之间相对静止，最多在夹角0~90度之间移动。
2）既然交流电产生的是一个旋转磁场，那么自然可以把它想像成一个直流电产生的恒磁场，只不过这个恒磁场处于旋转当中。
3）如果恒磁场对应的直流电流产生的磁场强度，与对应交流电产生的磁场强度相等，就可以认为两者等同。
4）坐标变换基于以上认知，首先认为观察者站在恒定磁场上并随之运转，观察被控磁场的直流电线圈电流及两个磁场之间的夹角。
5）实际的坐标变化计算出的结果有两个，直轴电流Id和交轴电流Iq。通过Id和Iq可以算出两者的矢量和（总电流），及两个磁场之间的夹角。
6）直轴电流Id是不出力的，交轴电流Iq是产生电磁转矩关键因素。
6. 对于交流同步隐极电动机(常见于交流伺服电机)：
1）其转子磁场是恒定的（由磁钢片决定）。
2）转子的当前磁极位置用旋转编码器实时检测。
3）定子磁极（旋转磁场）的位置从A相轴线为起点，由变频器所发的正弦波来决定。
4）实际上先有定子磁场的旋转，然后才有转子磁场试图与之对齐而产生的跟随。
5）计算出转子磁场与A相轴线之间的偏差角度。
6）通过霍尔元件检测三相定子电流，以转子磁场与A相轴线之间的偏差角度作为算子（相当于观察者与转子磁场同步旋转），通过坐标变换分解出定子旋转磁场中与转子磁极对齐的分量（直轴电流Id）,产生转矩的分量（交轴电流Iq）。
7）定子电流所产生旋转磁场与观察者基本同步，最多在夹角0~90度之间移动。移动量是多少，会体现在直轴电流Id、交轴电流Iq的数值对比上。
8）驱动器通过前面的速度环的输出产生电流环的给定，通过第6）条引入电流环的反馈Iq，通过PI控制产生Iq输出。
9）设定Id=0。这一点不难理解，使两个磁极对齐的电流我们是不需要的。通过这一点，我们实现了磁场定向FOC（控制磁铁之间角度为90度）。
10）计算出了Iq, Id=0。引入偏差角度算子通过坐标反变换变换产生了三相电流的输出。
11）当Iq>0, 定子旋转磁场对转子磁场的超前90度，电磁转矩依靠两个磁场之间异性相吸的原理来产生，这时候电磁转矩起到加速的作用。
12）当Iq<0, 定子旋转磁场对转子磁场的仍然超前90度，但是定子磁场的N、S极调换了一下，电磁转矩依靠两个磁场之间同性相排斥的原理来产生，这时候电磁转矩起到减速制动的作用。
13）从本质上讲，我们是依靠控制定子旋转磁场对转子磁场的夹角及该磁场的强度来实现矢量控制的。
7. 对于交流感应电动机（即异步电机）：
1）定子通入三相交流电，产生定子旋转磁场，旋转磁场以定子A相轴线为起点出发，并与定子电流相位对齐。
2）定子旋转磁场切割转子绕组，产生三相感应电势e=dλ/dt，λ为穿过转子绕组的磁链。e产生转子电流，然后产生另一个旋转磁场－－－－-转子旋转磁场。如果λ随空间（或时间）正弦变化，则e所产生的转子旋转磁场滞后穿越转子的旋转磁链90度。
3）转子旋转磁场的旋转速度叠加在旋转的转子上。事实上，这两个磁场之间的旋转是同步的。
4）与同步电机不同，感应电机的两个磁场之间不可能发生失步。因为转子速度一旦慢了，定子旋转磁场切割转子的速度就会加快，转子三相感应电势产生转子电流进而产生转子旋转磁场速度就必然加快。导致的结果仍然是两者同步。
5）感应电机的电磁转矩便由这两个磁场之间的试图对齐的力产生。
6）转子旋转磁场与转子电流对齐。
7）如果不考虑转子漏感的影响，转子为纯阻性负载，转子感应电势e与转子电流同相位。此时，这定子旋转磁场与转子旋转磁场之间的角度相差90度。
8）实际上，转子有漏感，且转差率越大，漏感越大，导致转子电流滞后转子电势一个角度，也就是说转子旋转磁场要比感应电势e滞后一个角度。
9）所以，受转子漏感的影响，我们无法保证定子旋转磁场和转子旋转磁场相差90度，它们之间相差的角度大于90度而小于180度。那么，我们就必须控制控制定子旋转磁场中与转子旋转磁场正交的部分，也就是穿过转子绕组的净磁链。
10）与同步电机的第1个区别在于，同步电机的转子磁场自然产生，因此定子上无需直轴电流来产生磁场（Id=0），只需控制交轴电流Iq。而感应电机的定子电流既需要直轴电流来产生定子旋转磁场，又需要交轴电流来产生转子旋转磁场。
11）与同步电机的第2个区别在于，感应电机矢量控制体现在保持定子磁场穿越转子绕组的部分强度恒定，控制转子电流自身产生的旋转磁场的大小。
12）转子起始磁极位置认为是0。在运转的过程中通过旋转编码器对其不断进行检测。为什么可以认为起始磁极位置=0，因为这一误差会随时间衰减到0。
13）定子磁极（定子旋转磁场）的位置从A相轴线为起点，由变频器所发的正弦波来决定。
14）计算出转子旋转磁极与A相轴线之间的偏差角度。
15）通过霍尔元件检测三相定子电流，以转子旋转磁场与A相轴线之间的偏差角度作为算子，通过坐标变换分解出其中产生与转子磁极对齐的分量（直轴电流Id）,产生转矩的分量（交轴电流Iq）。
16）保持Id为恒定值，即保证穿过转子绕组的净磁链恒定。
17）控制与Id相差90度的Iq大小，也就控制了转子旋转磁场的大小。
2008.12.22 首次发表
2008.12.26日更正部分错误。
2013.10.02 加入直流电机的铺垫，以利于理解。
引用 刘志斌 的回复内容：引用 煙雨朦朦 的回复内容：……现代控制理论，涉及到模式识别和自学习算法。……1、现代控制理论，涉及到模式识别和自学习算法，并不需要3-2、2-3变换；2、只要给电机通电，就可以检测和识别电机调速控制所需要的所有参数！3、用“现代控制理论”，来搪塞一切疑问和细节，就是“巫术”！
1、矢量控制可以用状态空间来表示，即可以用现代控制论方法来处理。实际电压模型、磁链方程、电流模型需要用到运算算子，也就是在正式的处理方法上，不是用经典控制理论方法来处理！但我在讨论上为了便于大家能在初等数学基础上可以了解，我用了更简单的方式进行了解释！矩阵变换一般也不属于经典控制论范围，所以我说他本质上是现代控制论范围！
2、只要给电机通电就能检测和识别电机调速控制的所有所有参数，你现在讲一个4KW4极电机同上电，可以告诉我电机的定子电阻、单抗、转子的电阻电抗、功率因数角、转动惯量、电机的重量、电机温度上升后定子和转子的电阻的变化？不是胡扯吗？没有电机模型，你根本没有办法计算出旋转坐标系和静止坐标系的夹角，也就不能应用矢量控制！
3、交流电动机矢量控制许多具有调谐功能，会自动计算电机参数，但是条件是必须有合适的模型才行。如果要更深理解矢量控制，就没有办法回避现代控制理论！
对待一个新的事物，我们应该首先来研究来学习，而不能用简单的类比或想当然加以否定，这才是正确的态度！
我只是想在问一句：
西门子SIMOVERT MASTERDRIVES是不是矢量控制变频器，LENZE9300是不是矢量控制变频器？
见过吗？用过吗？
只要回答是还是不是就行了，我相信论坛同行会做出自己的判断！够了到此为止吧！
对：煙雨朦朦关于 引用 刘志斌 的回复内容：引用 煙雨朦朦 的回复内容：……现代控制理论，涉及到模式识别和自学习算法。……1、现代控制理论，涉及到模式识别和自学习算法，并不需要3-2、2-3变换；2、只要给电机通电，就可以检测和识别电机调速控制所需要的所有参数！3、用“现代控制理论”，来搪塞一切疑问和细节，就是“巫术”！1、矢量控制可以用状态空间来表示，即可以用现代控制论方法来处理。实际电压模型、磁链方程、电流模型需要用到运算算子，也就是在正式的处理方法上，不是用经典控制理论方法来处理！但我在讨论上为了便于大家能在初等数学基础上可以了解，我用了更简单的方式进行了解释！矩阵变换一般也不属于经典控制论范围，所以我说他本质上是现代控制论范围！2、只要给电机通电就能检测和识别电机调速控制的所有所有参数，你现在讲一个4KW4极电机同上电，可以告诉我电机的定子电阻、单抗、转子的电阻电抗、功率因数角、转动惯量、电机的重量、电机温度上升后定子和转子的电阻的变化？不是胡扯吗？没有电机模型，你根本没有办法计算出旋转坐标系和静止坐标系的夹角，也就不能应用矢量控制！3、交流电动机矢量控制许多具有调谐功能，会自动计算电机参数，但是条件是必须有合适的模型才行。如果要更深理解矢量控制，就没有办法回避现代控制理论！对待一个新的事物，我们应该首先来研究来学习，而不能用简单的类比或想当然加以否定，这才是正确的态度！我只是想在问一句：西门子SIMOVERT MASTERDRIVES是不是矢量控制变频器，LENZE9300是不是矢量控制变频器？见过吗？用过吗？只要回答是还是不是就行了，我相信论坛同行会做出自己的判断！够了到此为止吧！ 内容的回复：
老兄别和他争了，浪费时间，就让他抱残守缺，聊度余生得了，反正也一把年纪了，让他去吧。
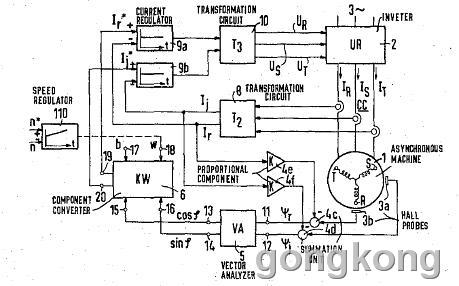
这张图是维基百科上摘下来的，1971年西门子的工程师F. Blaschke为矢量控制申请的专利。图上可以看出，那个时候的矢量控制还是有霍尔传感器来检测转子磁场相位的。个人觉得，要弄明白矢量控制，应该先从这张图开始，现在的矢量控制再怎么复杂，也是从这张图派生出来的。但是万变不离其宗，尽管已经过去了40几年，但是矢量控制的基本原理仍然是一脉相承的。
以下是维基百科中矢量控制的计算步骤：
1. Stator phase currents are measured, converted to complex space vector in (a,b,c) coordinate system.
测量定子电流，并使用（a，b，c）三相坐标系矢量来表示。
2. Current vector is converted to (
, 
) coordinate system. transformed to a coordinate system rotating in rotor reference frame, rotor position being derived by integrating the speed by means of speed measurement sensor.
将电流矢量换算为(, )坐标系，该坐标系是转子的参考坐标系，转子的位置可以使用速度传感器测量转速后积分得到。
3. Rotor flux linkage vector is estimated by multiplying the stator current vector with magnetizing inductance Lm and low-pass filtering the result with the rotor no-load time constant Lr/Rr, namely, the rotor inductance to rotor resistance ratio.
转子的磁链可以通过将定子电流乘以励磁电感Lm后经过低通滤波后得到，滤波器常数为转子空载时间常数Lr/Rr，即转子电感与转子电阻之比。
4. Current vector is converted to (d,q) coordinate system.
电流矢量换算到（d，q）坐标系。
5. d-axis component of the stator current vector is used to control the rotor flux linkage and the imaginary q-axis component is used to control the motor torque. While PI controllers can be used to control these currents,bang-bang type current control provides better dynamic performance.
d轴表示转子磁链，q轴表示电机转矩。可以使用PI控制器来控制这两个电流，bang-bang控制器可以得到更好的动态特性。
6. PI controllers provide (d,q) coordinate voltage components. A decoupling term is sometimes added to the controller output to improve control performance to mitigate cross coupling or big and rapid changes in speed, current and flux linkage. PI-controller also sometimes need low-pass filtering at the input or output to prevent the current ripple due to transistor switching from being amplified excessively and destabilizing the control. However, such filtering also limits the dynamic control system performance. High switching frequency (typically more than 10 kHz) is typically required to minimize filtering requirements for high-performance drives such as servo drives.
PI控制器可以算出对应于（d，q）坐标系的电压分量。将解耦后的分量加给电机，以提高控制性能，并降低互相耦合以及避免转速、电流和磁链的突变。PI可控制器的输入输出也可以加低通滤波器以避免电流纹波并使控制稳定。然而，滤波器会限制动态特性。在伺服上一般使用高频开关（10kHz以上）作为驱动，这样可以尽量不使用滤波器。
7. Voltage components are transformed from (d,q) coordinate system to (, ) coordinate system.
电压分量从(d,q)坐标系换算到(, )坐标系。
8. Voltage components are transformed from (, ) coordinate system to (a,b,c) coordinate system or fed in Pulse Width Modulation (PWM) modulator, or both, for signaling to the power inverter section.
电压分量从(, )坐标系换算到 (a,b,c)坐标系或使用脉宽调制PWM作为驱动，或两者同时使用，用以驱动功率模块。
Significant aspects of vector control application:
矢量控制的要点：
- Speed or position measurement or some sort of estimation is needed.
- Torque and flux can be changed reasonably fast, in less than 5-10 milliseconds, by changing the references.
- The step response has some overshoot if PI control is used.
- The switching frequency of the transistors is usually constant and set by the modulator.
- The accuracy of the torque depends on the accuracy of the motor parameters used in the control. Thus large errors due to for example rotor temperature changes often are encountered.
- Reasonable processor performance is required; typically the control algorithm has to be calculated at least every millisecond.
Although the vector control algorithm is more complicated than the Direct Torque Control (DTC), the algorithm is not needed to be calculated as frequently as the DTC algorithm. Also the current sensors need not be the best in the market. Thus the cost of the processor and other control hardware is lower making it suitable for applications where the ultimate performance of DTC is not required.
尽管矢量控制的算法比直接转矩控制（DTC）复杂，但是矢量控制的控制周期不需要像DTC那么短。并且不需要使用很好的电流传感器。所以处理器及其他控制硬件的成本相比同样性能的DTC会低很多。
引用 煙雨朦朦 的回复内容：
……回答问题要掌握基本要领：
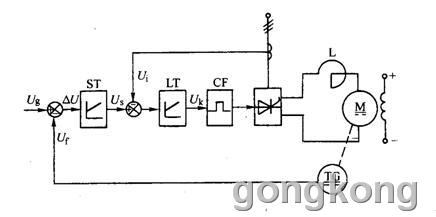
1、我指定了是三相可控硅全波整流的电枢主电路。
2、既然这样那么触发方式就一定是可控硅移相触发电路。我又约定为模拟电路，那么只有导线连接（印刷电路板也算），才能完成其功能。
3、电流调解器输出这个信号要么直接要么经过处理后必须连接到触发电路板的移相控制电压这个位置。这个端子应该与三角波输入（触发电路板由同步电压转换而成）在一个比较器的输入端进行比较，形成触发需要的脉冲。这个比较端还应该有一个偏置电压输入，以矫正触发角。如果这个触发板采用移相触发集成电路KJ004的KJZ6电路板必须接到A19端子。即使不知道具体的电路也应该回答一下几个要点：
（1）移相触发电路的移相触发控制端
（2）这是一个与三角波信号进行比较的比较端子当然你笼统说去了CF，而我要求的是具体去向，CF有那么多输入，比如同步电压也是输入到这个板，难道要跟同步信号进行比较吗？不讲出具体去向如何能从一个直流电平变成脉冲，当然是要和三角波进行比较后才行。可是我们从刘老师的回答，我们不能得到准确的信息！
1、速度反馈和电流反馈，最终都是调的直流电压的大小；
2、但是电流反馈解决的调速过程中电机启动、制动、负载突变、电流突变时存在的调速问题；
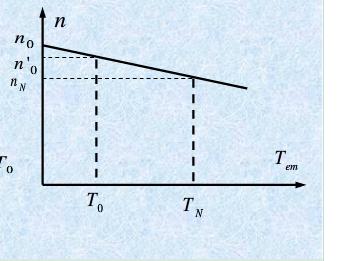
3、举例说，负载电流大时，电枢绕组压降IR大，由于（U-IR）/n=定值，电机速度偏离给定值就大，电流反馈的作用就是提高直流电压U，弥补IR造成的压降损失，使电机速度在控制要求范围内；
- 为什么变频器容易烧电机
[8560] - 关于变频器故障责任问题[5898]
- 请教：零线和地线共用接在变频...[9573]
- 电动自行车蓄电池在放电的同...[9195]
- 富士变频器报警ER1/ER2/ER3/...[8131]
- 富士变频器没有频率输出[5330]
- 为什么用西门子MM440变频器面...[9213]
- 变频器在工程应用中需要注意...[5769]
- VF控制和矢量控制的一些区别[28474]
- 请问：132KW的电机需要选择多...[6830]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
工控网智造工程师好文精选
