图解:采样,来认识一下呗! 点击:629 | 回复:3
图解:采样,来认识一下呗!
奈奎斯特采样定理,或者更准确地说是奈奎斯特-香农定理,是控制混合信号电子系统设计的基本理论原理。
正如我们所知道的,如果没有模数转换和数模转换,现代技术就不会存在。实际上,这些操作已经变得非常普遍了,以至于说“一个模拟信号可以转换成数字信号,然后再转换成模拟信号,而不会造成任何重大的信息损失”。
这听起来像是一种真理,但我们怎么知道情况确实如此呢?当它看起来似乎丢失了我们在单个样本之间观察到的如此之多的信号行为时,为什么还说采样是一种无损操作呢?
如图1所示,我们如何能从一个这样的信号开始:
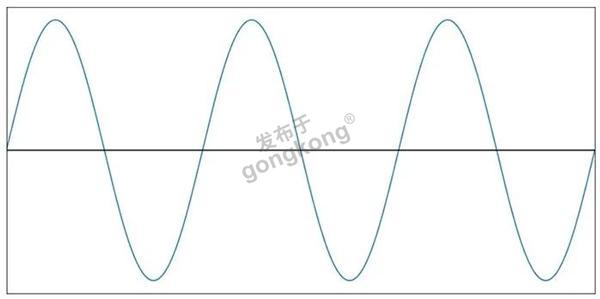
图1
再将其数字化成图2这样:
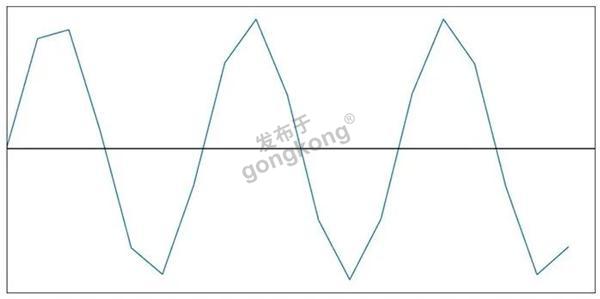
图2
然后还敢声称“原始信号可以恢复,且不会丢失信息”?
奈奎斯特-香农定理
请输入
之所以可以提出这样的说法,是因为它符合现代电气工程最重要的原理之一:
如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样,那么原始模拟信号就能从采样产生的离散值中完全恢复。
关于这个定理还有很多话要说,但首先,让我们试着弄清楚到底该怎么称呼它。
香农?奈奎斯特?科捷利尼科夫?惠特克?
请输入
我当然不是那个决定谁在阐述、论证,或者解释“香农-奈奎斯特-科特尔尼科夫-惠特克”采样和插值理论方面最值得赞扬的人。其实,这四个人都有参与其中,并且取得了显著成效。
但其中,哈里 · 奈奎斯特这个人的角色,似乎已经超出了它最初的意义。例如,在谭和江撰写的《数字信号处理:基本原理与应用》一书中,上述原理被确定为“香农采样定理” ;在塞德拉和史密斯的《微电子电路》一书中,我发现了下面这句话:“事实上,我们可以在有限数量的样本上进行处理……而忽略样本之间的模拟信号细节……这是基于香农采样定理。”
因此,我们或许应该避免使用“奈奎斯特采样定理”或者“奈奎斯特采样理论”这些词汇。如果我们需要把名字和这个概念联系起来,那么我建议只含有“香农”或者“奈奎斯特和香农”。事实上,也许是时候过渡到更匿名的东西了,比如“基本采样定理”。
如果你觉得这有点令人迷惑,请记住上面提到的采样定理与奈奎斯特速率是不同的,本文稍后将对此进行解释。我认为,没人能把奈奎斯特和他的速率分开,所以最终达成了一个很好的妥协:香农得到了定理,奈奎斯特得到了速率。
时域采样定理
请输入
如果我们将采样定理应用于频率f信号的正弦波,就必须要对f样本≥2f信号的波形进行采样才能实现完美重构。换句话说,每个正弦周期至少需要两个样本。接下来,让我们先从时域的角度来理解一下这句话。
在下面这张图中,正弦波的采样频率远远高于信号频率:
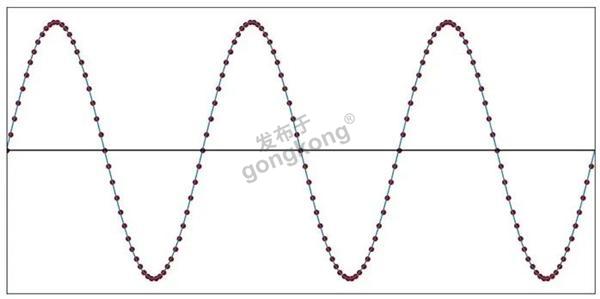
图3:每个圆点代表一个采样瞬间,即测量模拟电压后,并将其转换为数字的精确时刻
为了更加直观地了解这个采样过程,我们可以绘制采样值,然后用直线将它们连接起来。如下图所示的直线近似值看起来与原始信号完全相同:相较于信号频率,采样频率非常高,因此线段与相应的曲线正弦波线段没有明显的差异。

图4
但随着我们降低采样频率,直线近似值的外观与原始图像有所不同了。
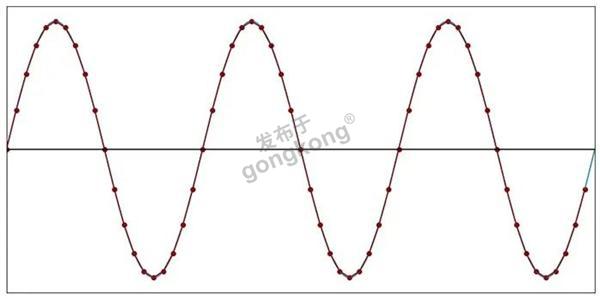
图5:每个周期20个样本(f样本=20f信号)
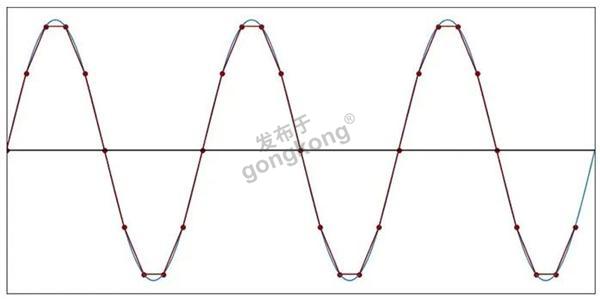
图6:每个周期10个样本(f样本=10f信号)

图7:每个周期5个样本(f样本=5f信号)
当f样本=5f信号时,离散时间波形不再是连续时间波形的理想表现了。但是,请注意,我们仍然可以清楚地识别离散时间波形的频率,信号的周期性并没有消失。
临界值:每个周期2个样本
请输入
随着我们把每个周期的采样数量减少到5个以下,采样产生的数据点仍将继续保持模拟信号的循环性质,但最终会达到一个频率信息被破坏的点。首先,考虑下面的情节:
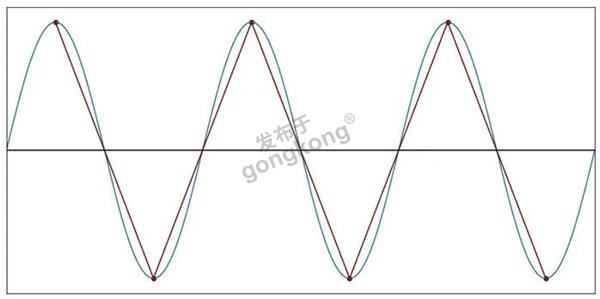
图8:每个周期2个样本(f样本=2f信号)
当f样本=2f信号时,正弦曲线完全消失了。但是,由采样数据点产生的三角波并没有改变正弦曲线的基本周期性,三角波的频率与原始信号的频率相同。
然而,一旦我们将采样频率降低到每个周期少于2个样本时,这种说法就不再成立了。因此,在混合信号系统中,对于原始信号中的最高频率,每个周期2次采样是至关重要的临界值,其对应的采样频率就称为奈奎斯特速率:
如果我们以低于奈奎斯特速率的频率对模拟信号进行采样,那么将无法完美地重构原始信号。
下面两张图显示了当采样频率低于奈奎斯特速率时所发生的周期性等效损失:
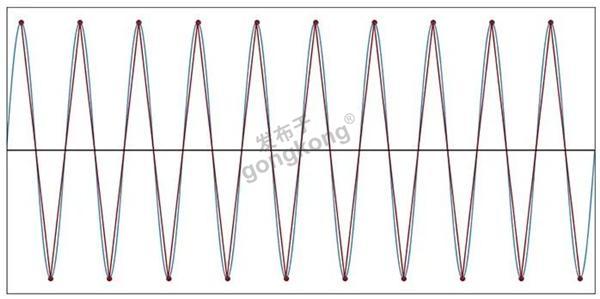
图9:每个周期2个样本(f样本=2f信号)
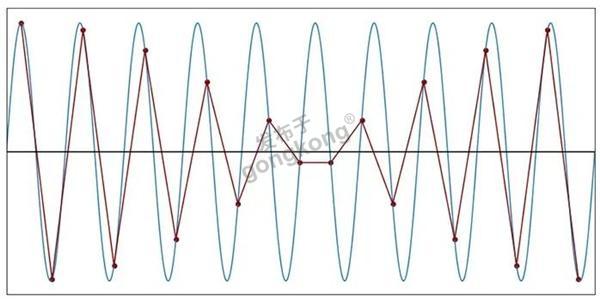
图10:每个周期1.9个样本(f样本=1.9f信号)
当f样本=1.9f信号时,离散时间波形基本上获得了全新的周期性行为。采样模式的完全重复,需要一个以上的正弦波周期。
然而,当我们每个周期只有1.9个样本时,采样频率不足的影响就有点难以解释了。接下来的情节,更清楚地说明了这一切:
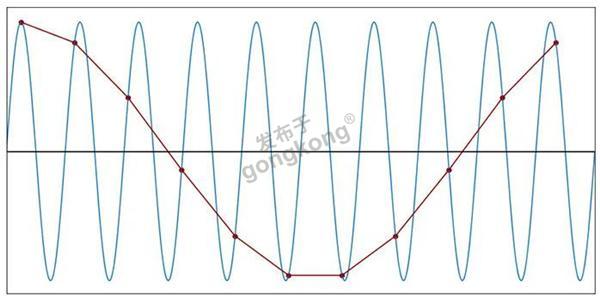
图11:每个周期1.1个样本(f样本=1.1f信号)
如果你对正弦波一无所知,并且使用1.1f信号采样产生的离散时间波形进行分析,那么你将会对原始信号的频率产生严重的错误想法。此外,如果你只有离散数据,那么就不可能知道频率特性已经被破坏了。采样产生了一个原始信号中不存在的新频率,但你不知道这个频率不存在。
奈奎斯特采样定理,或者更准确地说是奈奎斯特-香农定理,是控制混合信号电子系统设计
 正在下载,请等待……
正在下载,请等待……
楼主最近还看过
奈奎斯特采样定理,或者更准确地说是奈奎斯特-香农定理,是控制混合信号电子系统设计的基本理论原理。
正如我们所知道的,如果没有模数转换和数模转换,现代技术就不会存在。实际上,这些操作已经变得非常普遍了,以至于说“一个模拟信号可以转换成数字信号,然后再转换成模拟信号,而不会造成任何重大的信息损失”。
这听起来像是一种真理,但我们怎么知道情况确实如此呢?当它看起来似乎丢失了我们在单个样本之间观察到的如此之多的信号行为时,为什么还说采样是一种无损操作呢?
如图1所示,我们如何能从一个这样的信号开始:
图1
再将其数字化成图2这样:
图2
然后还敢声称“原始信号可以恢复,且不会丢失信息”?
奈奎斯特-香农定理
请输入
之所以可以提出这样的说法,是因为它符合现代电气工程最重要的原理之一:
如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样,那么原始模拟信号就能从采样产生的离散值中完全恢复。
关于这个定理还有很多话要说,但首先,让我们试着弄清楚到底该怎么称呼它。
香农?奈奎斯特?科捷利尼科夫?惠特克?
请输入
我当然不是那个决定谁在阐述、论证,或者解释“香农-奈奎斯特-科特尔尼科夫-惠特克”采样和插值理论方面最值得赞扬的人。其实,这四个人都有参与其中,并且取得了显著成效。
但其中,哈里 · 奈奎斯特这个人的角色,似乎已经超出了它最初的意义。例如,在谭和江撰写的《数字信号处理:基本原理与应用》一书中,上述原理被确定为“香农采样定理” ;在塞德拉和史密斯的《微电子电路》一书中,我发现了下面这句话:“事实上,我们可以在有限数量的样本上进行处理……而忽略样本之间的模拟信号细节……这是基于香农采样定理。”
因此,我们或许应该避免使用“奈奎斯特采样定理”或者“奈奎斯特采样理论”这些词汇。如果我们需要把名字和这个概念联系起来,那么我建议只含有“香农”或者“奈奎斯特和香农”。事实上,也许是时候过渡到更匿名的东西了,比如“基本采样定理”。
如果你觉得这有点令人迷惑,请记住上面提到的采样定理与奈奎斯特速率是不同的,本文稍后将对此进行解释。我认为,没人能把奈奎斯特和他的速率分开,所以最终达成了一个很好的妥协:香农得到了定理,奈奎斯特得到了速率。
时域采样定理
请输入
如果我们将采样定理应用于频率f信号的正弦波,就必须要对f样本≥2f信号的波形进行采样才能实现完美重构。换句话说,每个正弦周期至少需要两个样本。接下来,让我们先从时域的角度来理解一下这句话。
在下面这张图中,正弦波的采样频率远远高于信号频率:
图3:每个圆点代表一个采样瞬间,即测量模拟电压后,并将其转换为数字的精确时刻
为了更加直观地了解这个采样过程,我们可以绘制采样值,然后用直线将它们连接起来。如下图所示的直线近似值看起来与原始信号完全相同:相较于信号频率,采样频率非常高,因此线段与相应的曲线正弦波线段没有明显的差异。
图4
但随着我们降低采样频率,直线近似值的外观与原始图像有所不同了。
图5:每个周期20个样本(f样本=20f信号)
图6:每个周期10个样本(f样本=10f信号)
图7:每个周期5个样本(f样本=5f信号)
当f样本=5f信号时,离散时间波形不再是连续时间波形的理想表现了。但是,请注意,我们仍然可以清楚地识别离散时间波形的频率,信号的周期性并没有消失。
临界值:每个周期2个样本
请输入
随着我们把每个周期的采样数量减少到5个以下,采样产生的数据点仍将继续保持模拟信号的循环性质,但最终会达到一个频率信息被破坏的点。首先,考虑下面的情节:
图8:每个周期2个样本(f样本=2f信号)
当f样本=2f信号时,正弦曲线完全消失了。但是,由采样数据点产生的三角波并没有改变正弦曲线的基本周期性,三角波的频率与原始信号的频率相同。
然而,一旦我们将采样频率降低到每个周期少于2个样本时,这种说法就不再成立了。因此,在混合信号系统中,对于原始信号中的最高频率,每个周期2次采样是至关重要的临界值,其对应的采样频率就称为奈奎斯特速率:
如果我们以低于奈奎斯特速率的频率对模拟信号进行采样,那么将无法完美地重构原始信号。
下面两张图显示了当采样频率低于奈奎斯特速率时所发生的周期性等效损失:
图9:每个周期2个样本(f样本=2f信号)
图10:每个周期1.9个样本(f样本=1.9f信号)
当f样本=1.9f信号时,离散时间波形基本上获得了全新的周期性行为。采样模式的完全重复,需要一个以上的正弦波周期。
然而,当我们每个周期只有1.9个样本时,采样频率不足的影响就有点难以解释了。接下来的情节,更清楚地说明了这一切:
图11:每个周期1.1个样本(f样本=1.1f信号)
如果你对正弦波一无所知,并且使用1.1f信号采样产生的离散时间波形进行分析,那么你将会对原始信号的频率产生严重的错误想法。此外,如果你只有离散数据,那么就不可能知道频率特性已经被破坏了。采样产生了一个原始信号中不存在的新频率,但你不知道这个频率不存在。
所以,最终结论是:当我们以低于奈奎斯特速率的频率采样时,信息就会永久地丢失,原始信号无法完美地重构。
结语
请输入
本文讨论了香农采样定理和奈奎斯特速率,并且试图通过观察采样在时域中的影响来深入了解这些概念。在下一篇文章中,我们将从频域的角度来探讨这个话题。
最后,需要说明一下,由于个人能力有限,有些词句可能翻译得比较生硬,建议有英文阅读能力的小伙伴儿一定要去阅读原文。另外,文中翻译如有不当之处,还请批评指正。
- 求瓦萨变频器中的传感器
 [1043]
[1043] - 谁能告知导电塑料位移传感器...
 [628]
[628] - PC机能把红外光电开关的信号...
 [1662]
[1662] - 怎样判断电流传感器
 [1025]
[1025] - 电容式物位计有哪些选用原则...
 [1080]
[1080] - 防爆传感器工作原理
 [1339]
[1339] - 距离设定反射型和限定反射型...
 [1480]
[1480] - HEIDENHAIN、FAGOR 资料?
 [1321]
[1321] - 安川、明电舍变频器
 [1136]
[1136] - 选择接近开关
 [1487]
[1487]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号




















 工控网智造工程师好文精选
工控网智造工程师好文精选
