基于六西格玛降低超细粉自动控制系统故障时间 点击:1002 | 回复:0
在降低超细粉自动控制系统故障时间的项目实践过程中,天行健咨询专家依据六西格玛管理的方法论,关注每个工序和指标参数对故障时间的影响,聚焦到多个问题点,进而系统性的分析问题、分解项目,针对不同的问题,使用了六西格玛的多种工具综合加以解决,而且每个工具和分析方法的使用都可以根据实际问题灵活运用,最终取得了良好的效果,为维护行业精细化水平的提高提供了新思路。

1、使用假设检验对程序优化前后进行比较
首先建立假设:改进后故障时间的平均值是否显著降低?通过改进前、后故障时间的平均值的单值图和箱线图粗略地可以看出有所降低,为了准确,继续研究P值。经双样本T检验后,P值=0.000<0.05,故障时间的平均值确实有所降低,因此改进有效。

2、全因子试验设计
通过A阶段得出磨机的稳定性对超细粉自动控制系统运行影响显著;而通过I阶段分析可知辊压设定和风量设定两个参数对磨机的稳定性影响比较大。我们要判断哪个因子的主效应显著?哪个因子的交互效应显著?什么条件下可以获得最佳的运行稳定性?则需要通过DOE试验来得出结论(每个参数试验时间为1d)。
辊压:低水平为94 bar,高水平为98 bar。
风量:低水平为845 r/min,高水平为855 r/min。
准备做全因子试验重复4次,中心点4次试验。
①参数试验设计分析
从方差分析表中可以看出,辊压和风量的P值=0.000<0.05,说明辊压和风量对磨内压差影响显著,相互间的二阶交互P值全部为0.000,说明相互间的二阶交互作用对磨内压差影响显著。主效应项P值=0.000<0.05,说明模型有效。弯曲项p值=0.824>0.05,说明模型无弯曲。

②参数试验设计残差分析
观察以观测值顺序为横轴的散点图,残差无不正常的升降趋势;观察响应变量拟合值的散点图,残差无“漏斗型”或“喇叭型”,此图正常;残差服从正态分布。由残差分析,可以判断实验模型合适。
③参数试验设计分析(回归方程式)
磨内压差的系数估计,使用未编码单位的数据。
回归方程式为:磨内压差=1440.2-15.2906辊压-1.70375风量+0.018125辊压x风量。
④主效应和交互效应分析
从辊压、风量的主效应图可以看出,辊压、风量均与磨内压差成正比关系,从交互效应图可以看出,两条线不平行,说明辊压和风量存在交互作用。
⑤等值线图、响应曲面图(见图3)
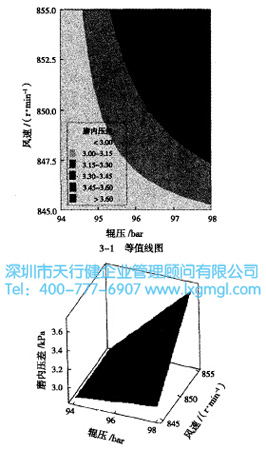
从磨内压差与辊压、风量的等值线图上看出,辊压在94-98 bar之间取值,风速在845-855 r/min之间取值,磨内压差能达到理想要求。
从磨内压差与辊压、风量的曲面图上看出,曲面有扭曲现象,说明风量与辊压存在交互作用。
⑥实现最优化
通过调优,当辊压为94 bar,风速为845 r/min时,磨内压差能达到理想要求。
楼主最近还看过
- 化工行业导入六西格玛培训公...
 [1007]
[1007] - 六西格玛咨询项目在某公司的...
 [887]
[887] - 年赚20亿每周开店3家,创始人...
 [474]
[474] - 北京X桥梁建设公司FMEA培训心...
 [1055]
[1055] - 廊坊水泥厂利用TPM设备管理降...
 [449]
[449] - 销售如同恋爱,换个思维更容易...
 [482]
[482] - 六西格玛在电子商务物流行业...
 [750]
[750] - 东莞机械工厂导入精益生产管...
 [1304]
[1304] - 江苏精益生产培训公司怎么选...
 [673]
[673] - 如何通过张驰精益生产培训,提...
 [666]
[666]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号

















 工控网智造工程师好文精选
工控网智造工程师好文精选
