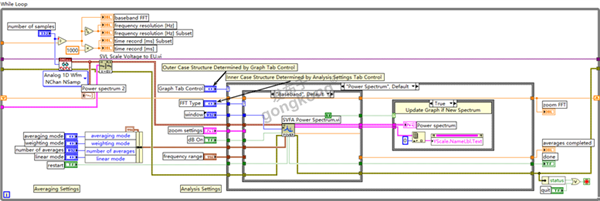
Power Spectrum.vi

• 功能：对输入波形进行功率谱分析，计算信号在各频率点的功率分布。

• 使用场合：需分析信号频率域功率特性，如识别信号主要频率成分、噪声分布等场景。

• 特点：集成了窗函数、平均等处理，提升功率谱分析精度；结果直观反映信号功率的频率分布。

• 使用注意事项：窗函数选择需匹配信号特性（如汉宁窗适合一般频谱分析，矩形窗适合精准频率测量）；平均次数影响谱的平滑度与统计特性，需根据需求调整。

• 类似功能对比：比手动实现功率谱计算（如自行做 FFT 后求模平方等）更快捷，内置算法经过优化；与其他第三方功率谱分析工具相比，与 LabVIEW 整体环境集成更紧密，数据流转更顺畅。

FFT (Mag - Phase).vi

• 功能：对输入信号进行快速傅里叶变换（FFT），得到信号的幅度 - 相位频谱，即各频率分量的幅度和相位信息。

• 使用场合：需获取信号频率分量的幅度与相位细节，如分析信号相位特性、进行相干分析等场景。

• 特点：基于 FFT 算法高效计算，能快速得到频域幅相信息；结果可直观展示信号的频率构成及相位关系。

• 使用注意事项：输入数据长度宜为 2 的幂次（如 256、512 等），以提升 FFT 计算效率；相位分析易受噪声等影响，需结合信号实际情况解读。

• 类似功能对比：相较于手动编写 FFT 算法（如蝶形算法实现），该 VI 调用简单，计算效率经专业优化；与其他 FFT 工具（如 MATLAB 中的 fft 函数）相比，在 LabVIEW 环境下无需数据格式转换，实时性更好。

Power Spectral Density.vi

• 功能：计算信号的功率谱密度（PSD），反映单位频率内的功率分布，可用于分析随机信号的频谱特性。

• 使用场合：分析噪声、振动等随机信号的频率域能量分布场景。

• 特点：能准确表征随机信号的频谱能量特性；支持不同平均和窗函数处理，提升分析可靠性。

• 使用注意事项：需明确信号是随机还是确定性的，PSD 更适用于随机信号；平均方式和窗函数选择对 PSD 结果影响较大，需合理设置。

• 类似功能对比：比功率谱更能精准反映随机信号的频谱能量密度；与手动计算 PSD（结合 FFT、窗函数、平均等步骤）相比，该 VI 集成度高，操作简便。

DAQmx Clear Task.vi

• 功能：清除已完成的 DAQ 任务，释放相关硬件资源。

• 使用场合：数据采集任务结束后，需释放资源，避免资源占用影响其他任务或系统运行时。

• 特点：确保硬件资源被正确释放，保障系统长期稳定运行；与 DAQmx 任务创建流程配套，实现资源闭环管理。

• 使用注意事项：任务清除前需确保任务已停止，避免强制清除导致硬件异常；多任务场景下需按顺序清除，防止资源依赖冲突。

• 类似功能对比：相较于不释放资源直接结束程序，能有效避免硬件资源泄漏；与旧版资源释放方式相比，更符合 DAQmx 任务化管理，释放更彻底。

FFT 详细说明

原理

系统中应用

关键要点

• 频率分辨率：频率分辨率 \(\Delta f=\frac{f_s}{N}\)，其中 \(f_s\) 是采样率，N 是采样点数。频率分辨率决定了能区分的最小频率间隔，若要提高频率分辨率，可增加采样点数 N 或降低采样率 \(f_s\)（需注意满足奈奎斯特采样定理）。

• 窗函数影响：为减少频谱泄漏（因信号截断导致的频谱扩散），FFT 前通常会对信号加窗（如汉宁窗、矩形窗等）。不同窗函数对主瓣宽度、旁瓣衰减的影响不同，需根据分析需求选择，例如汉宁窗旁瓣衰减大，能有效抑制泄漏，但主瓣较宽；矩形窗主瓣窄，频率测量更精准，但旁瓣衰减小，泄漏较严重。

• 相位特性：FFT 得到的相位是相对相位，且受信号起始相位、窗函数等因素影响。在分析相位相关问题（如信号间的相位差）时，需注意这些影响因素，必要时进行相位校准或结合实际信号源特性分析。