欧姆定律的进化 点击：2220 | 回复：62
我们是用正弦交流电的“电压有效值”与“电流有效值”之比来定义的“阻抗”（阻抗可以是感抗也可以是容抗还可以是电阻、电感、电容三种性质掺杂着的合成阻碍作用）。但是，作为讲课老师的刘志斌，却把眼光局限在正弦交流电的一个个“瞬时值”上，所以他误以为在我们日常使用中的正弦交流电路中固定电感的感抗和固定电容的容抗都是变化不定的。
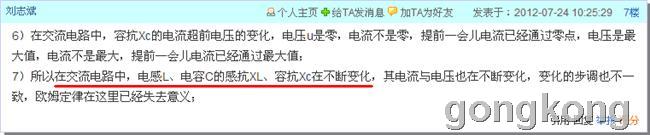
刘志斌说：“7）所以在交流电路中，电感L、电容C的感抗XL、容抗Xc在不断变化，其电流与电压也在不断变化，变化的步调也不一致，欧姆定律在这里已经失去意义；”
为什么刘志斌会得出这个错误结论呢？其原因是：刘志斌没有搞懂正弦电路里对“阻抗”的定义是从正弦电压、电流“有效值”层面去定义的。他不知道电工通常讲的正弦交流电压、电流都是指“有效值”，他不知道正弦电路里所用的电压表、电流表都是以“有效值”来刻度的！
事实上，世界各国的正弦交流市电都是稳定的标准频率。尽管有些国家的工频标准是60Hz，有些国家的工频标准是50Hz 。但是，在具体的一个电力系统中这个工频标准是一定的！
电源的频率不变，固定电感、固定电容的电抗难道是如刘志斌说的在“不断变化”吗？！
客观事实告诉我们：正弦电路中固定电感、固定电容的电抗是电源频率的函数，但并不是正弦量瞬时值的函数，即：只要电源频率稳定不变的前提下，电抗是不会随正弦量瞬时值而变化的！
欧姆定律难道真如刘志斌诋毁的那样“在（正弦交流电路）这里已经失去了意义”吗？！
否！在正弦电路里，从“有效值”的层面去看欧姆定律，欧姆定律依然光芒万丈！
一段无源正弦交流电路的“电压最大值”与“电流最大值”之比也叫这段电路的“阻抗”，这是有依据的。这种依据是客观事物的自然哲学之数学原理。正弦电压与电流的最大值之比等于“阻抗”是一种必然，而并非如这刘志斌所瞎掰的“巧合”！
我们举例说明电路的自然哲学之数学原理决定了正弦“电压最大值”与正弦“电流最大值”之比，同样也具有表征电路对正弦电流的阻碍作用的意义：
一个电感线圈，其等效电路为电感L与电阻R串联的一段无源电路。我们设：这段无源电路中的电流 i(t)=Imsinωt ，则,电感L因电流 i(t)随时间的变化而产生“自感电势eL(t)”。
eL(t)=-L(di/dt)＝-ImωLcosωt＝ImωLsin(ωt-π/2)
我们知道，电感上的电压 u(t)与这个自感电势eL(t)大小相等方向相反：
u(t)=L(di/dt)＝ImωLcosωt＝ImωLsin(ωt+π/2)
u(t)=Umsin(ωt+π/2) 且：u(t)=ImωLsin(ωt+π/2)
比较上面俩式即可得出：Um=ImωL 即：Um与Im成正比，比例系数为：ωL
即证明：电感上的正弦“电压最大值”与线圈中的“电流最大值”之比ωL也同样具有表征电感对正弦电流的阻碍作用的意义。（ωL即：电感的“感抗XL”），
Um/Im＝ωL＝XL
同理，我们也可以证明电容上的正弦“电压最大值”与通过电容的正弦“电流最大值”之比(1/ωC)也同样具有表征电容对正弦电流的阻碍作用的意义。（“1/ωC”即：电容的“容抗Xc”），
Um/Im＝1/(ωC)＝Xc
请大家注意：
1、这里的“感抗XL”和“容抗Xc”都是“阻抗”这个概念的外延。
2、我们是说，正弦电压最大值与电流最大值之比，也同样具有表征电路对正弦电流的阻碍作用的意义。
3、“感抗XL”和“容抗Xc”只在正弦电路中才有意义，而且XL和Xc都不等于电压和电流瞬时值的比值。
刘志斌之所以跟我们死犟说：“7）所以在交流电路中，电感L、电容C的感抗XL、容抗Xc在不断变化，其电流与电压也在不断变化，变化的步调也不一致，欧姆定律在这里已经失去意义；”是因为刘志斌没有弄懂《电工学》对交流电路“阻抗”的定义！
刘志斌误以为正弦交流电路的“阻抗”是交流电的“电压瞬时值”与“电流瞬时值”之比。他认为“瞬时值”不停的变化，所以正弦交流电路的“感抗XL”和“电抗Xc”就在“不断变化”。
但事实却是：对于指定频率、指定电路参数的正弦交流电路来说，其“感抗XL”、“容抗Xc”是确定不变的！因为 XL=ωL ，Xc=1/(ωC)，它们只与正弦电流的角频率ω (ω=2πf)以及电路的“电感量L”、“电容量C”有关，而与电压、电流之“不断变化”的瞬时值却是无关的。
请注意：《电工学》对正弦交流电路的“阻抗”的定义是：正弦交流“电压有效值”与“电流有效值”之比叫做交流电路的“阻抗”。
刘志斌的认知与科学体系的概念不相同。他完全站在一个与我们所谈论的“交流电路的欧姆定律”不同的层面上理解问题，所以要跟我们死犟说欧姆定律在交流电路里已经失去了意义。
- 学习PLC的感受
[2001] - 用户如何控制伺服位置环计数...[2624]
- 【5.11更新】2022待答疑帖，期待...[18158]
- 化学及化工专业英语词汇[3224]
- 电位器怎么接在变频器上[3263]
- BACnetScan使用手册[2939]
- 电工的相关知识[2013]
- SIEMENS PLC常用英语缩写表[3195]
- OPCServer使用说明[3494]
- 电气工程师手册下载[9213]
官方公众号
智造工程师
-
客服
-
小程序
-
公众号
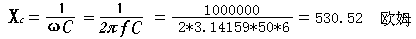
工控网智造工程师好文精选
