介绍LabVIEW 的Polynomial Roots和1D Rational Polynomial Evaluation VI，通过分析系统传递函数 \(p(z) = \frac{b(z)}{a(z)}\) 的零极点，判断系统稳定性。可修改多项式系数 a、b 观察对稳定性的影响。

系统稳定性在离散系统中，依据传递函数极点是否都在单位圆内判断。若所有极点位于单位圆内，系统稳定；否则不稳定。零极点分布还会影响系统的幅频、相频特性。

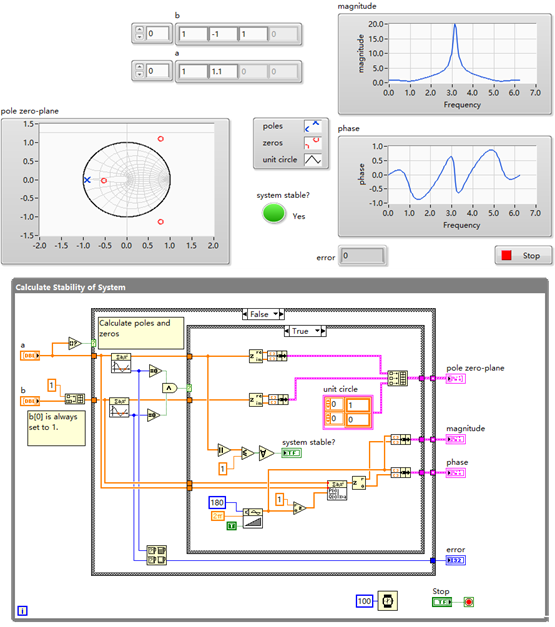
VI 说明

• Polynomial Roots VI

• 功能：计算多项式的根（即系统的零极点）。

• 使用场合：需要获取多项式零点、极点（如分析系统零极点分布以判断稳定性）时使用。

• 特点：能高效求解多项式根，为系统分析提供基础数据。

• 使用注意事项：输入的多项式系数需准确，否则根的计算结果会出错，进而影响后续稳定性判断。

• 类似功能对比：与手动求解多项式根相比，该 VI 自动化程度高、计算速度快且不易出错；和其他数值计算库的根求解函数相比，更贴合 LabVIEW 的图形化编程环境，使用更便捷。

• 1D Rational Polynomial Evaluation VI

• 功能：对有理多项式（即两个多项式的比值，如传递函数 \(\frac{b(z)}{a(z)}\)）进行求值，可得到系统在不同频率下的幅值、相位等特性。

• 使用场合：需要分析系统频率响应（幅频特性、相频特性）时使用。

• 特点：可快速计算有理多项式在指定点的取值，方便获取系统的频率域特性。

• 使用注意事项：输入的分子、分母多项式系数要与实际系统传递函数对应，且需合理设置求值的频率范围，以准确反映系统特性。

• 类似功能对比：相较于手动计算有理多项式在各频率点的取值，该 VI 效率高、准确性好；和专用的频率响应分析工具相比，它更灵活，可与 LabVIEW 其他模块结合，进行自定义的系统分析。

在控制工程领域，离散系统的稳定性分析是设计稳定控制系统的关键步骤。LabVIEW 作为图形化编程环境，通过这些专用 VI，更便捷地进行系统分析与设计，无需深入复杂的数值计算细节，专注于系统本身的特性研究与优化。