贝塞尔函数matlab处理 点击:643 | 回复:2
楼主最近还看过
在电机三维模型的解析法求解过程中,修正的贝塞尔函数(Modified Bessel Functions)的应用确实可能导致数值上的挑战,特别是当函数的自变量和阶数变化时。这些函数通常在解决电磁场问题时用于处理边界条件和解析解。
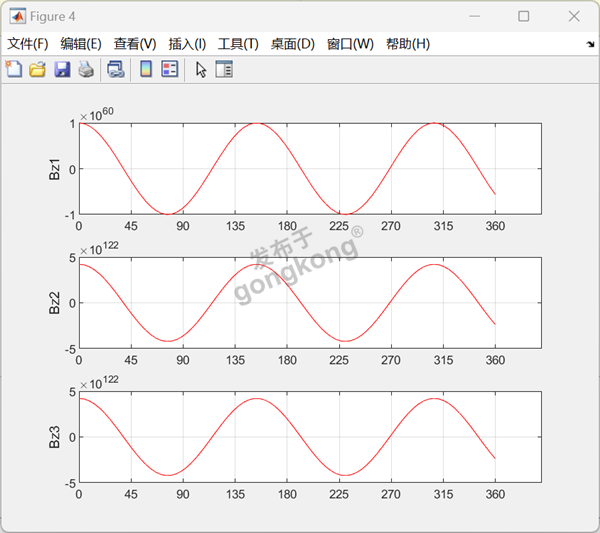
当遇到气隙磁密异常大的问题时,通常需要从以下几个方面进行考虑和调整:
检查输入参数:
确保贝塞尔函数的输入参数(如自变量和阶数)在合理的范围内,并且没有错误的输入。
特别注意阶数,它可能是影响函数值的关键因素。在某些情况下,阶数可能非常大,导致数值不稳定。
数值稳定性:
修正的贝塞尔函数在某些情况下可能表现出数值不稳定性。考虑使用更稳定的算法或实现方式。
对于大阶数或特定自变量范围,可能需要使用特殊技术来确保数值精度和稳定性。
边界条件:
检查电机模型的边界条件是否设置正确。错误的边界条件可能导致数值解的不稳定或异常。
模型验证:
验证你的解析模型是否与其他已知方法或实验结果相符。如果存在差异,可能需要重新审查模型的假设和推导过程。
归一化或缩放:
如果可能的话,尝试对模型或解进行归一化或缩放,以减小数值差异并提高稳定性。
使用软件库:
考虑使用现有的数学软件库(如MATLAB、SciPy等)来计算修正的贝塞尔函数。这些库通常经过优化,可以提供更稳定和准确的数值结果。
网格细化:
如果你的解析模型涉及到离散化或网格化,尝试细化网格以提高数值解的精度。
文献调研:
查阅相关领域的文献,看是否有其他研究者遇到过类似的问题,并了解他们是如何解决的。
专业咨询:
如果问题仍然无法解决,考虑咨询电机工程或电磁场领域的专家,他们可能能提供更具体的建议。
最后,需要强调的是,解析法虽然具有其独特的优势(如解析表达式的清晰性和物理意义的直观性),但在处理复杂问题时可能存在一定的局限性。在某些情况下,数值方法(如有限元法)可能更为适用和可靠。因此,根据具体问题的特点选择合适的求解方法也是非常重要的。

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号



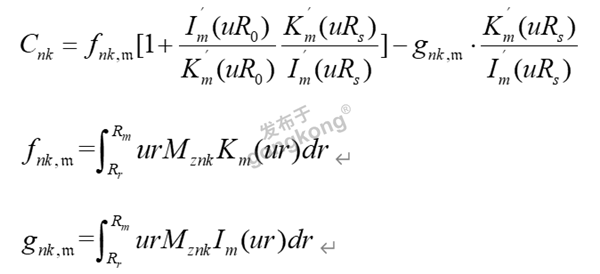
















 工控网智造工程师好文精选
工控网智造工程师好文精选
