随着测试测量过程中数字仪器的普及,获取海量数据变得愈发容易,但如何从数据中提取有效信息成为挑战。曲线拟合技术通过建立数学模型,揭示观测值与独立变量间的关系,可实现噪声抑制、函数建模、数据插值与外推等功能。本文系统介绍 LabVIEW 中的曲线拟合模型、算法及应用案例。
曲线拟合目标:为数据集(xi,yi)寻找函数f(x),使加权残差∑wi[yi−f(xi)]2最小。
关键参数:
| VI 名称 | 适用模型 | 典型应用场景 |
|---|
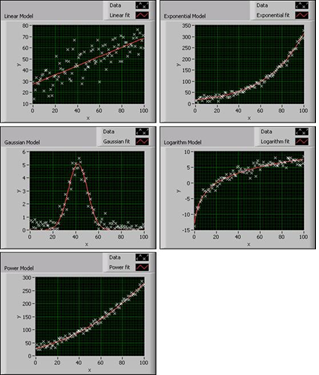
| Linear Fit | 线性模型y=ax+b | 传感器校准、趋势分析 |
| Exponential Fit | 指数模型y=aebx | 衰减过程、生物生长曲线 |
| Gaussian Peak Fit | 高斯模型 | 信号峰值检测、光谱分析 |
| Logarithm Fit | 对数模型y=aln(x)+b | 非线性响应建模 |
| Power Fit | 幂函数模型y=axb | 材料应力 - 应变关系 |
通用多项式拟合
通用线性拟合
三次样条拟合
通过平衡参数p(0-1)控制平滑度与拟合度。
p=0:线性插值;p=1:严格插值。
非线性拟合
拟合优度指标:
置信区间与预测区间:
置信区间:参数估计的不确定性范围(图 9 左)。
预测区间:未来测量值的置信范围(图 9 右)。
通过多项式拟合建立温度计误差模型(表 2),补偿后误差降低至原值的 1/10(图 11)。
使用通用多项式拟合提取 ECG 信号基线(图 12),相比小波分析更高效。
结合分水岭算法与非线性椭圆拟合,修复遮挡物体的边缘检测(图 14)。
基于通用线性拟合分解遥感影像中的水体、植被与土壤成分(图 16)。
通过误差函数 VI 实现 LabVIEW 未内置的指数修正高斯模型(图 17)。
LabVIEW 提供从基础线性到复杂非线性的全流程曲线拟合工具,支持噪声处理、参数优化与结果验证。实际应用中需结合数据特性选择模型(如 LS 适合高斯噪声,Bisquare 适合含异常值数据),并通过预处理与后评估提升拟合精度。对于特殊需求,可利用自定义函数扩展 LabVIEW 的拟合能力。
术语对照表
| 英文术语 | 中文翻译 |
|---|
| Least Squares | 最小二乘法 |
| Levenberg-Marquardt | 列文伯格 - 马夸尔特算法 |
| R-square | 决定系数 |
| Confidence Interval | 置信区间 |
| Prediction Interval | 预测区间 |
| Outlier | 异常值 |



 客服
客服


 小程序
小程序


 公众号
公众号





 客服
客服


 小程序
小程序


 公众号
公众号

