倾角测量的典型应用

在乘用车上，电动驻车制动器(EPB)被用于使汽车在平坦的分级道路上保持静止。这是通过用一个单轴或双轴加速度计测量倾角来实现的。一般做法是将一个X轴/Y轴或Z轴低g加速度计装在EPB控制单元中一个专门的模块中。现在，越来越多的汽车配有ESC（电子稳定控制）功能，在单个芯片中集成了组合式低g加速度计和陀螺仪。这样做是为了防止汽车侧滑和翻车；ESC功能已经成为世界各国或地区法律的强制要求。

如果通过组合器件（单芯片、组合式加速度计和陀螺仪）实现倾角测量，则不必在车上安装一个独立的EPB模块，结果可以大幅降低汽车的成本。由于组合器件通常用于ESC，所以并未针对倾角检测优化，并且通过组合器件测量倾角时，测量精度有时无法达到要求。由于组合器件是XY轴或XYZ轴，所以通常用X轴进行倾角测量，EPB模块中的部分传统型低-g加速度计使用的是Z轴，因为它是垂直安装在发动机舱里的。检测轴应该与重力垂直，才能取得更高的精度——我们稍后会讨论这一点。

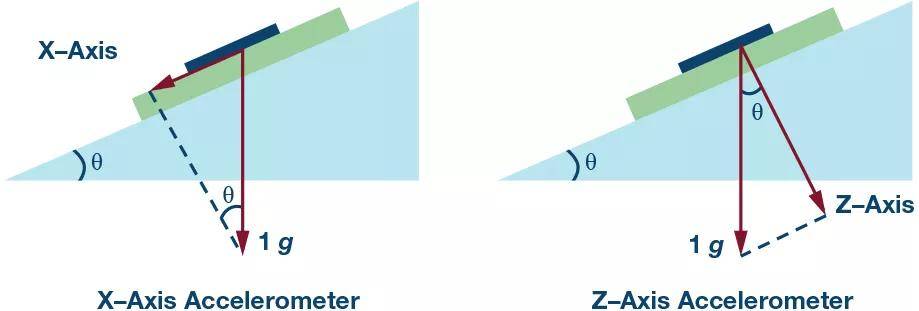
图1. X轴和Z轴加速度计的安装示意图。

对于汽车中的倾角测量，评估精度是非常重要的。不妨想像，您的车停在绝对平坦的地面，因此，加速度计计算的倾角应该是0°。如果您的车停在斜坡上，就应该精确地检测出倾角，以便正确地激活刹车系统。

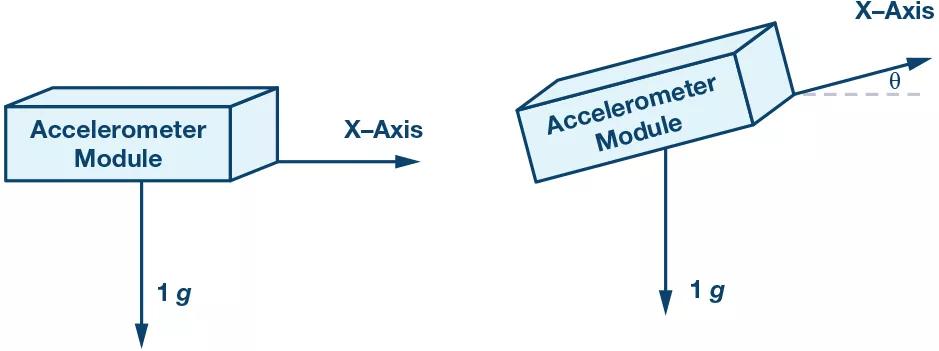
图2. X轴检测倾角测量示意图。

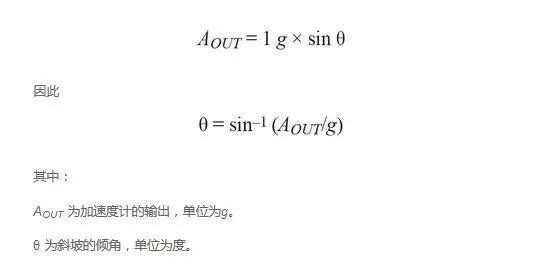
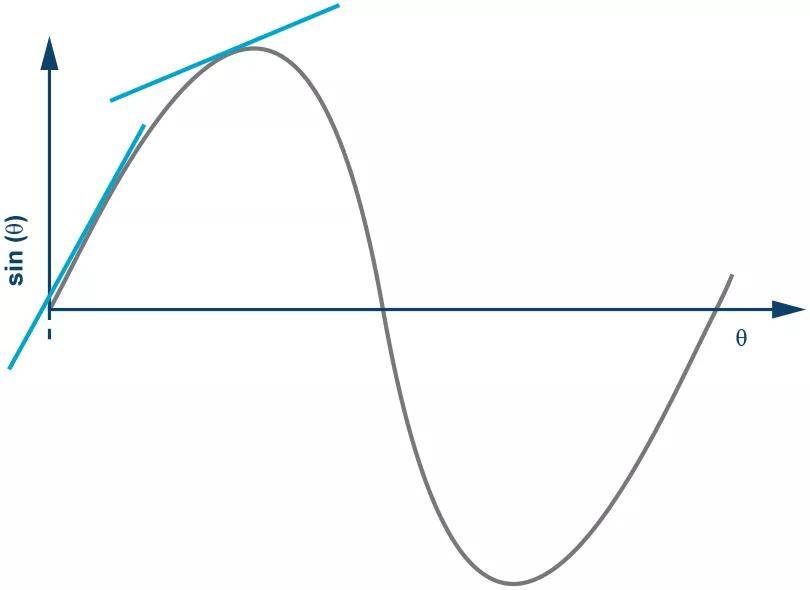
图3. sinθ对θ随θ增大而下降的灵敏度。

由于sin θ是一个非线性函数，所以，AOUT与θ之间的关系是非线性的，在接近零时其线性度处于最佳状态，即其此时具有最佳的测量精度。随着θ的增大，测量精度下降。这正是检测轴应与重力垂直的原因，因为道路坡度将接近零。

对于汽车倾角测量，不必在全斜坡坡度的条件下考虑系统。现实世界中，道路上的绝大多数斜坡坡度不会超过30°。我们只需要分析在±30°的范围内分析贡献因素的精度即可。

影响系统级测量精度的贡献因素有多个：

●灵敏度误差和初始绝对失调

●非线性度

●与初始绝对失调的总失调变化

●噪声

1、灵敏度误差和初始绝对失调

灵敏度误差

灵敏度是对输入-输出测得的传递函数的斜率，通常为+1g和–1g。灵敏度误差为器件间的灵敏度偏差。例如，有些加速度计的最大灵敏度为3%。

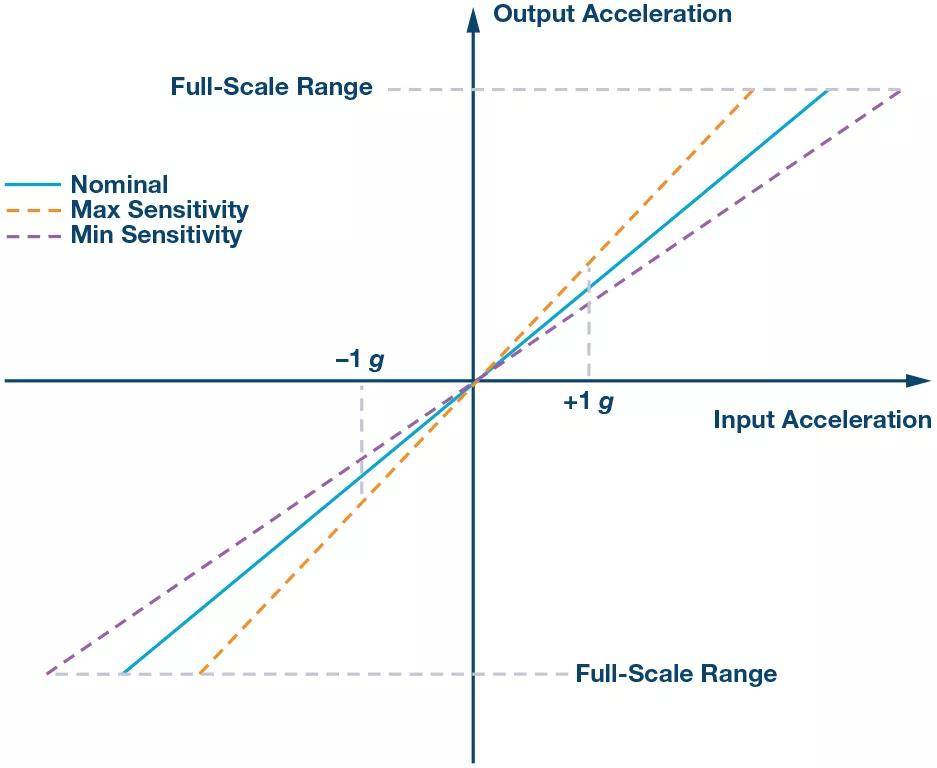
图4. 输入-输出加速度灵敏度误差。

初始绝对失调

范围内的失调约为25℃；例如，在模块制造完成后立即测量的值为25℃±5℃。初始绝对失调表示大量器件的实测偏移值的标准差。

两点校准

对于倾角测量应用，两个主要的误差来自失调误差和灵敏度误差。这两种误差会导致不可接受的检测结果，因此不得忽略。如果我们希望消除这些部分误差，则应对加速度输出进行校准。一般地，要对倾角测量的失调和灵敏度进行一次校准。若要考虑失调和灵敏度误差，则加速度计输入与输出的关系为：

有两种基本校准技术；其中一种是单点校准。这种校准的具体做法是在加速度计上施加一个0g场，然后测量输出。这类校准只能用于校准失调误差，不能校准增益误差。然后，从实际输出值中减去0g场里的输出结果，消除失调误差。这种校准方法非常简单，但精度不足，因为仍然存在灵敏度误差。另一种方法是1g翻转校准，在+1g和–1g时采用两点校准，并在每个+1g和–1g场内按照以下公式测量加速度输出：

2、非线性度

器件的非线性度为测得加速度(AMEA)与理想线性输出加速度(AFIT)之间的最大偏差。加速度测量数据集应包括加速度计的满量程范围。其测量方式为Max(|AMEA – AFIT|)。

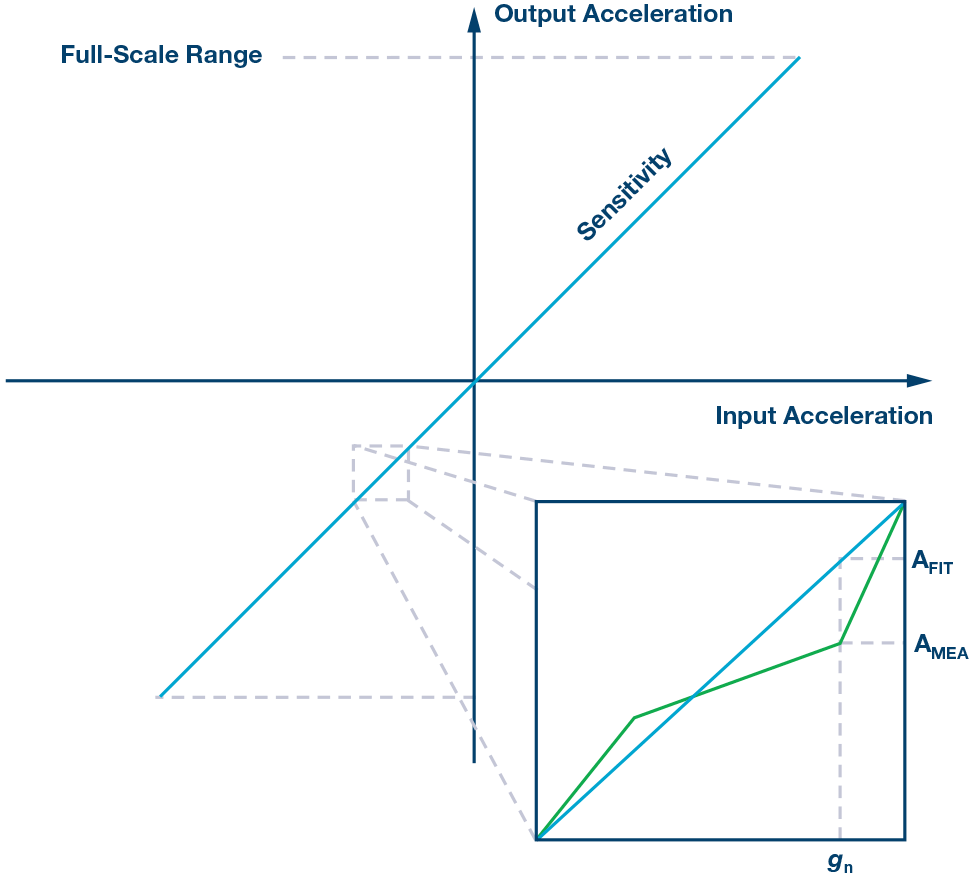
图5. 器件非线性度。

其中：

AMEA为给定gn下的测得加速度。

AFIT为给定gn下的预测加速度。

多数加速度计或组合器件在给定输入加速度计范围内均存在非线性——例如，30 mg ± 2g的范围。对于倾角测量应用，输入坡道斜率在±30°以内，这意味着输出加速度范围在±500 mg (±1g× sin 30°)以内，所以应重新评估该范围内的非线性度。由于非线性度在整个输入范围内是非线性的，所以，很难准确地量化评估这部分误差。然而，由于该器件的数据手册通常都很保守，线性度为30 mg，输入范围为±2g，用10 mg计算±500 mg范围内的误差更合理些。

3、与初始绝对失调的总失调变化

与初始绝对失调的总失调变化为温度、应力和老化效应导致的失调的最大偏差。该偏差是相对于给定器件的初始绝对失调进行测量的。这是精度总误差的主要贡献因素。

在温度、应力、老化等所有这些因素中，变化与温度在总失调变化中占比很大。一般地，变化与温度曲线是二阶曲线，通常为旋转抛物线。为了消除这部分误差，可以在系统级执行三点校准。对于给定器件，可按下列步骤校准输出失调随温度的变化值。

第1步：

使器件的输出响应以某个 ∆N0值偏移。温度校准流程的第一步是 消除环境温度下的失调。

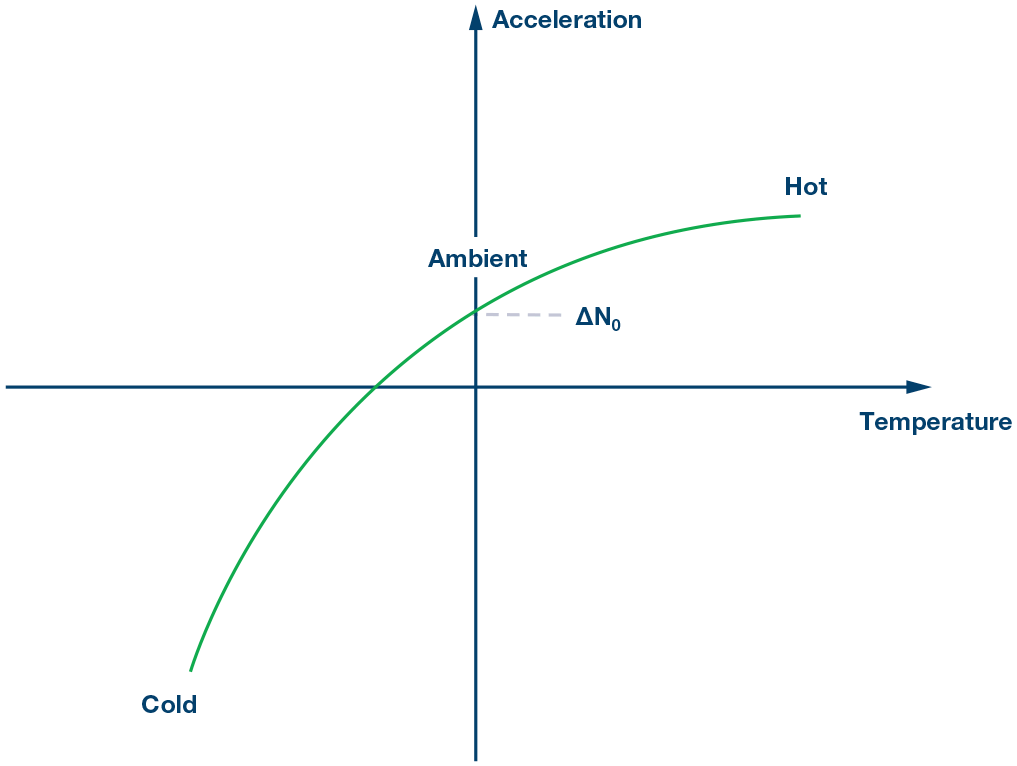
图6. 第1步：消除环境温度下的失调。

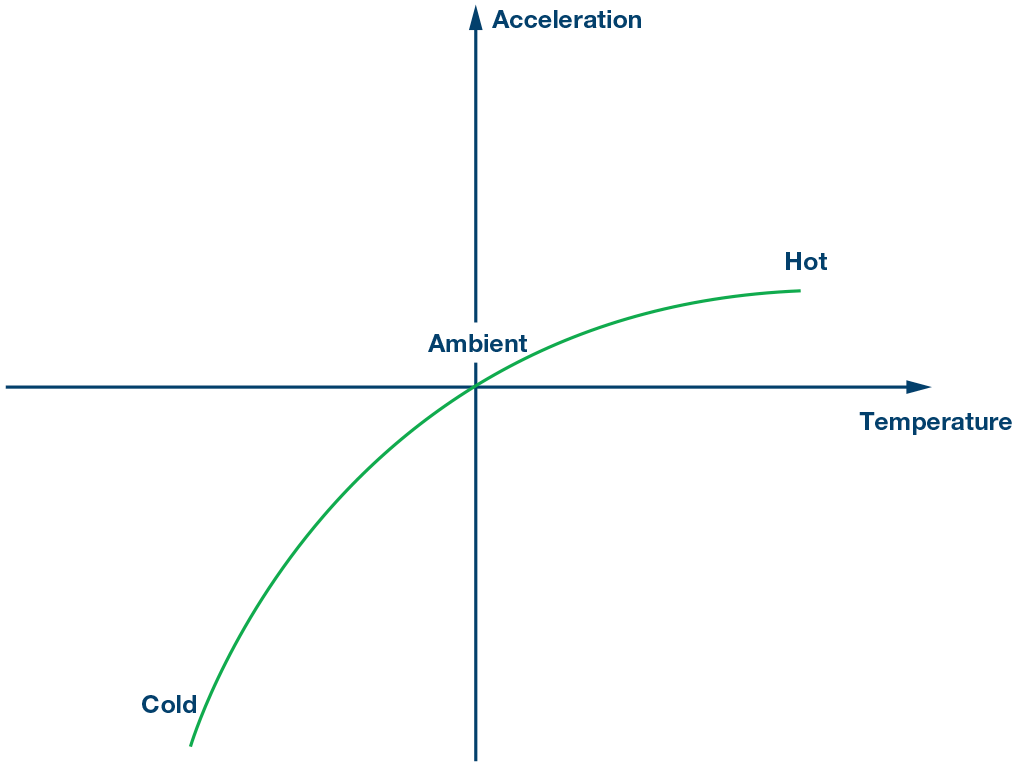
图7. 第2步：在消除环境温度下的失调之后。

第2步：

接下来，在高温下测试器件，用获得的新信息生成失调校正线性公式。

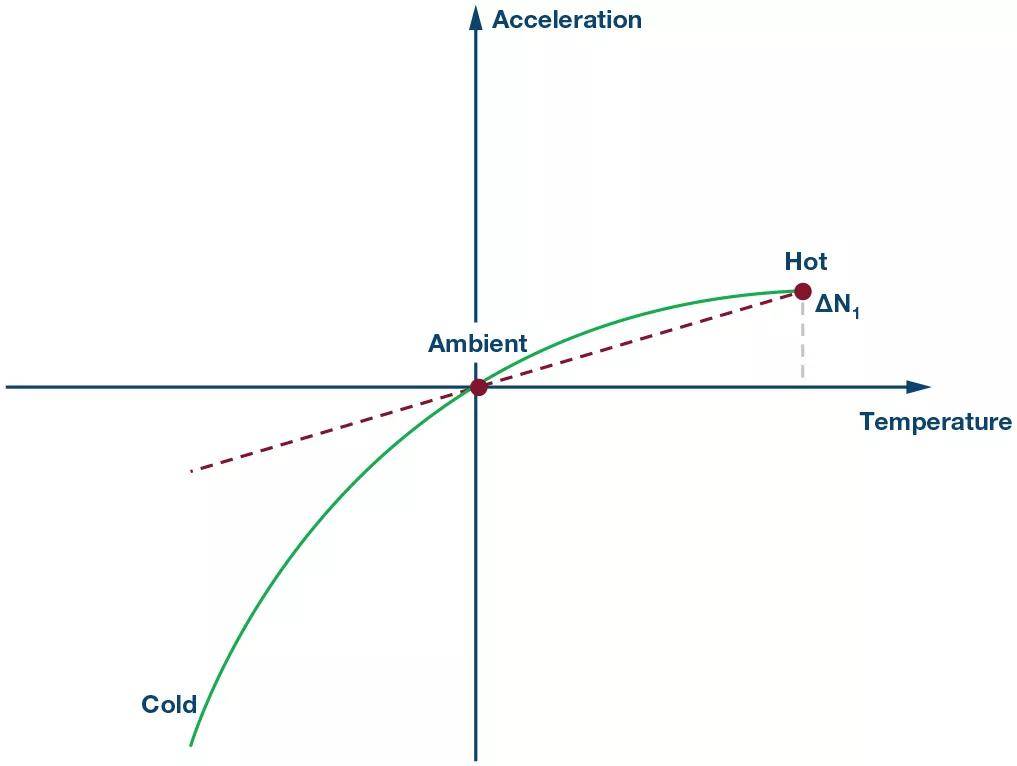
图8. 第3步：消除高温下的抛物线旋转分量。

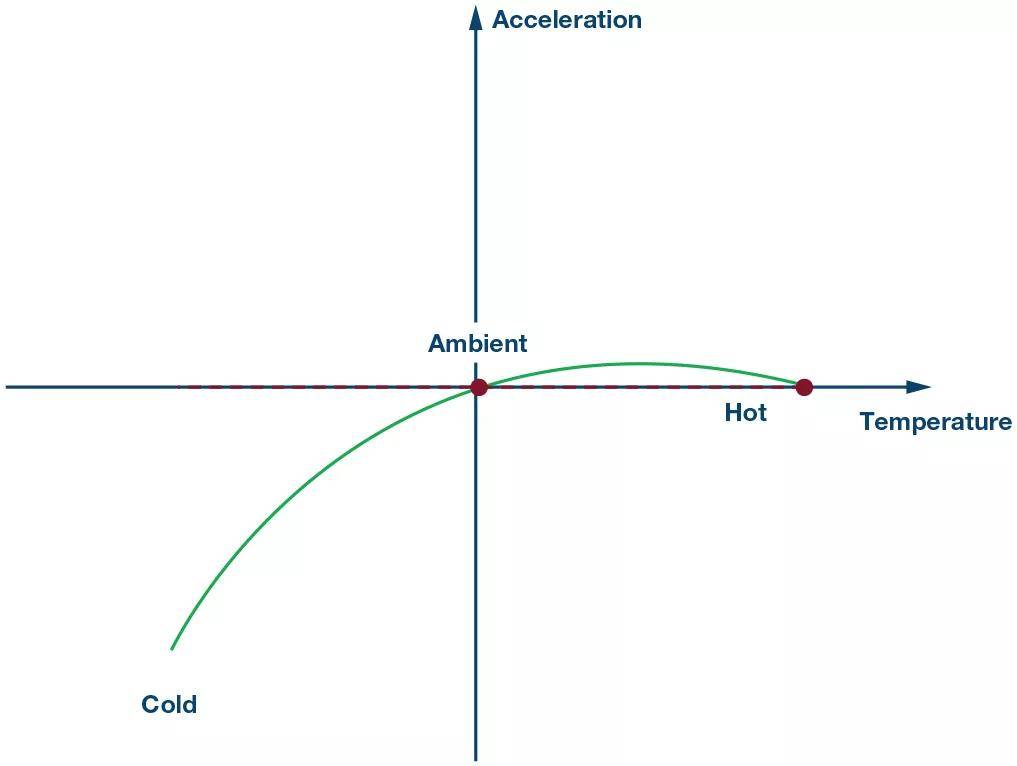
图9. 第4步：在消除高温下的抛物线旋转分量之后。

第3步：

给现有公式添加一个二阶分量，校正失调剩余部分。设二阶曲线遵循以下公式：

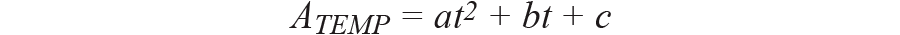
这是二阶抛物线公式，已经通过第1步和第2步消除了旋转分量。

在该公式中，该二阶抛物线有三个解：

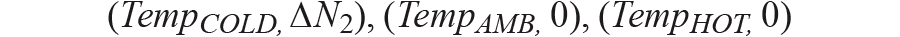
然后，我们可以得到温度系数 a, b, c.

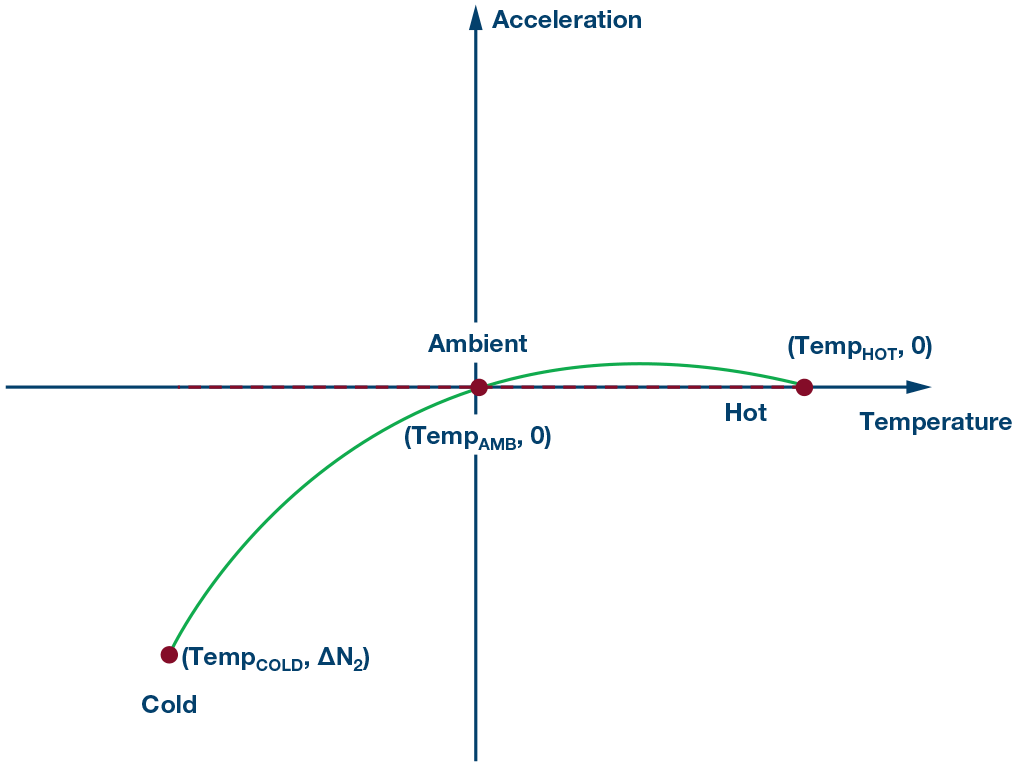
图10. 第5步：添加二阶分量，消除剩余失调。

有关△N0, △N1, △N2, a, b, c 的所有温度系数信息应该存储在系统非易失性存储器中，同时需要一个板载温度传感器。系统会在每次上电后例行校准加速度计，确保消除失调随温度的变化值。

4、噪声

基于单个数据样本测量倾角不一定可靠。即使加速度计的噪声为零，倾角测量也是在汽车启动时测量的，所以，需要减小发动机、过往车辆或乘客在车上来回移动导致的任何振动。最好的办法是在不降至最低数据速率要求的条件下，在尽量长的时间内做数据平均。数据平均算法会减少rms噪声。

假如我们对噪声采样，结果可得到每个样本的方差

以上推导显示，对同一未校正噪声的n次实现求均值可使噪声功率减少n倍，并使rms噪声减少√n。

由于随机噪声受高斯分布影响，所以，rms噪声等于高斯分布的标准差。6σ以内的最小分布为97%。

例如，如果以1 kSPS的采样率对每100 ms的数据求均值，则最大rms噪声 = 0.4 mg，即是说如果以6σ作为与平均值的距离，则此时的峰值噪声仅为2.4 mg。

用于与rms值相乘的因数取决于器件要执行的任务的统计需求。例如，如果选择6作为因数（峰峰值噪声为6 × RMS_Noise），则算法在器件生命周期内要运行的次数会影响超过最差情况6 × RMS_Noise 的概率。可总结如下：

E=M×r

E为在生命周期内超过最差情况的预期次数，M为生命周期内的运行次数，r为超过最差情况的概率。基于此，我们可以通过乘以rms噪声评估出一个合理的因数。