微积分方程拉开了现代数学和现代物理的序幕，具有里程碑的意义。反正就是一个很牛逼的东西。在座的各位，哦不，在看的各位，我敢说十有八九都是一脸懵逼的进来。

但我，必须不能让各位一脸懵逼的出去。

微分的解释在书上说的很详细，各种啪啪啦啦的描述，我可以详细的把他们摘录下来。但这明显有违我的初衷，因为我摘录下来很多人也看不懂，包括我自己。但从各种书刊论文的字里行间中我隐约地看出两个字符，那就是dy/dx。

我们可以认为一个函数在某一点的微分方程解就是该点的Y向量除以该点的X向量。

1. 

导数微分的描述为dy/dx。

2. 

3. 

微分,实质还是极限。

4. 

示波器可以极快的分割波形的X和Y向量，所以可以用示波器来验证波形的微分方程解。

我选用FreeTest的示波器来做详解。大家也可以称它为"牛顿.莱布尼兹.示波器"。

Freetest无线示波器

SIN的微分解

先来上一个基础的sin(a)波形。这个大家应该都知道微分方程解是cos(a)。什么？你不知道，那就假装知道吧，给我一个台阶下。

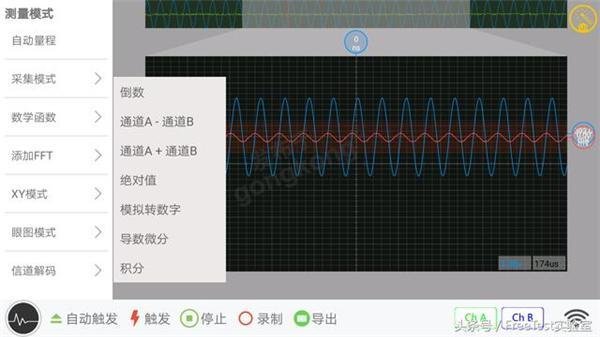
示波器内置的数学运算

图中，蓝色波形是采集的sin正弦波信号，红色是经过示波器微分处理后的cos信号。

详细的数学求解公式来一波。学霸的往下看，和我一样是学渣的直接跳过看结果。

<sin的微分求解过程开始>

(sina)'=lim(b->0)[sin(a+b)-sina]/b

因为sin(a+b)=sinacosb+cosasinb

这里b无穷小,有cosb=1.

于是lim(b->0)[sin(a+b)-sina]/b

=lim(b->0)[cosasinb]/b

当b无穷小,有sinb/b=1.所以

lim(b->0)[sin(a+b)-sina]/b =cosa

<sin的微分求解过程完成>

结论：和示波器显示的完全一样，cos(a)。

直线的微分解

我们知道常量的微分解是0，那么，直线的微分解呢？

测量直线波形并求微分（三角波的一个斜率）

结论：直线的微分方程是一个常量。

这个的求解过程我就不发出来了，怕被各位嘲笑。

三角波的微分解

三角波是由两条直线组成，按照直线的微分是一个常量的描述，那么三角波的微分就应该是两个不同的常量间隔组成。来，上图验证下。

三角波及其微分运算结果

结论：三角波的微分是个方波。

方波的微分解

方波可以认为是常量加跃变合成的波形，按照"微分,实质还是极限"这个定义来看，常量部分应该是0，然后上升沿部分应该是个正脉冲，下降沿部分应该是个负脉冲。

方波及其微分运算结果

结论：上面的推论是正确的。

指数的微分解

指数函数稍微复杂点。

指数函数及其微分运算结果

我们排除跃迁部分，单看一个周期的指数函数。可以发现，红色微分波形其实也是一个指数函数，但变化幅度没有原本指数变化的快。

结论：指数函数的微分解为(a^x)'=a^xlna。

洛伦兹脉冲

高斯线型和洛伦兹线型是常用在光谱中描述峰形状的曲线。

洛伦兹线型函数的简单形式为：L=1/(1+x^2)。

如上图所示。但微分方程我暂时不会解。

调频正弦波

结论：调频正弦波的微分解是个调频余弦波。这个大家可以尝试着思考下。

我们再来看几个方程式比较复杂的波形，这个我就不简述他们的求解过程了。

辛克脉冲

多级合成波

噪声

噪声其实是最复杂的方程组集合，当然其微分解也必然是各种方程组的集合。结果，看起来就又是一个噪声了。

-----------------

最后，看看使用的设备是什么：

泰思科技的无线示波器

看起来还是非常便携方便