PLC对输入输出模拟量的编程的讨论与解析 点击:30002 | 回复:17
PLC对输入输出模拟量的编程的讨论与解析
对于初学PLC编程的人来说,模拟量输入、输出模块的编程要比用位变量进行一般的程序控制难的多,因为它不仅仅是程序编程,而且还涉及到模拟量的转换公式推导与使用的问题。不同的传感变送器,通过不同的模拟量输入输出模块进行转换,其转换公式是不一样的,如果选用的转换公式不对,编出的程序肯定是错误的。
模拟量信号有温度、压力、流量等不同的物理量,他们通过变送器将其模拟量的最小值~最大值转换为电压或电流二种信号输出:1、电压信号,输出有 0~10V,或0~5V等;2、电流信号,输出有 4~20ma。
传感变送器将这二种信号输送给PLC,PLC再通过模拟量输入模块,再将这二种信号转换为与之成比例变化的数字量,以PT100温度传感变送器为例,其测量温度范围为0~100度,对应输出为4~20ma电流信号,即0度对应输出电流为4 ma,100度对应输出电流为20 ma,该信号输送给S7-200的模拟量输入输出模块EM235。此时应将EM235的模拟量输入设置为0~20ma,这样当输入0~20ma信号给EM235的模拟量输入端时,EM235将其电流信号转换为0~32000的数字量。即:1ma对应数字量为:32000÷20=1600,故当输入4~20 ma 电流信号给EM235的模拟量输入端时,EM235转换的数字量为6400~32000。被测温度T与对应转换的数字量AIW0的关系如下图一:
如变送器测温0~100度,其输出为0~5V的电压信号,EM235输入设置应为0~5V,输入0~5V信号给EM231的模拟量输入端时,EM231将0~5V电压信号也转换为0~32000的数字量。即:1V对应数字量为:32000÷5=6400,被测温度T与对应转换的数字量AIW0的关系如下图二:
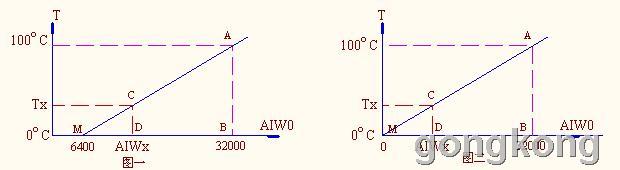
一、转换公式的推导
见上图一:温度=0度时,对应数字量=6400(即M点坐标),温度=100度时,对应数字量=32000(即A点坐标),当实测温度Tx ,它对应的数字量=AIWx,即图中C点坐标。显然△MCD与△MAB相似,故可列:

式(2)、式(4)皆为转换公式,但二者公式不一样,其原因:图一、图二的关系曲线不一样,图一的关系曲线为不通过坐标原点的直线,而图二的关系曲线是通过坐标原点的直线,使用时不能弄错,否则会造成计算错误。
式(2)中的AIWx为EM235将变送器输送来的被测温度对应的电流Ix转换成与之成比例的数字量,式(4)中的AIWx为EM235将变送器输送来的被测温度对应的电压Vx转换成与之成比例的数字量,PLC可以根据变送器的实际输出形式,选用按(2)或(4)式的运算进行编程即可求出被测温度值Tx.
二、按转换公式编程:
根据转换后变量的精度要求,对转换公式编程有二种形式:1、整数运算,2、实数运算。
下面梯形图是按整数与实数进行运算的编程:
(A)、按式(2)进行整数运算的梯形图:
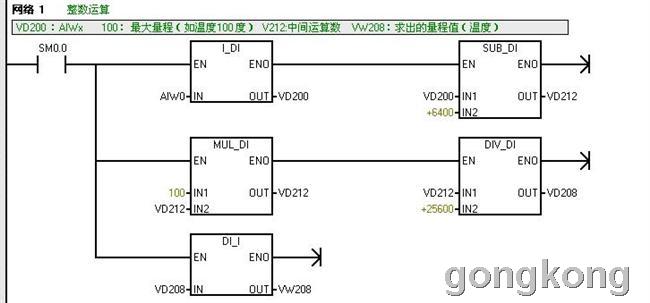
该梯形图是第(1)种 温度传感变送器(测温:0~100度 ,输出:4~20ma)按公式(2)以整数运算编写的转换程序,它可作为一个子程序进行调用。
(B)按式(2)进行实数运算的梯形图:

该梯形图是第(1)种 温度传感变送器(测温:0~100度 ,输出:4~20ma)按公式(2)以实数运算编写的转换程序,可作为一个子程序进行调用。
C、按式(4)进行整数运算的梯形图:
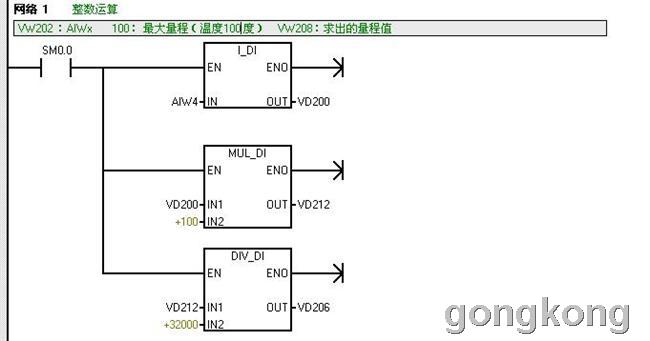
该梯形图是第(2)种 温度传感变送器(量程:0~100度,输出:0~5V)按公式(4)以整数运算编写的转换程序,可作为一个子程序进行调用。
D、按式(4)进行实数运算的梯形图:
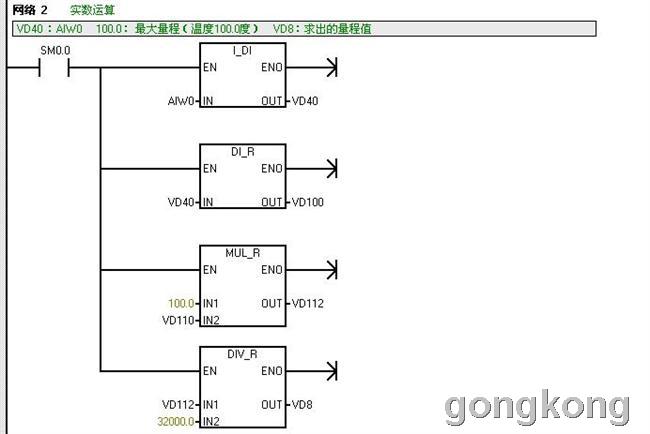
该梯形图是第(2)种 温度传感变送器(量程:0~100度,输出:0~5V)按公式(4)以实数运算编写的转换程序,可作为一个子程序进行调用。
三、对模拟量输出的编程处理
对模拟量输出的编程本文选用简单一个实例:一电动阀门,其输入控制信号为4~20ma,即对其输入4ma时,阀门关闭,当输入20 ma 时,阀门全打开。控制要求:按下启动按钮,阀门应线性的由关闭到全打开,控制时间为50秒。
硬件选择:选用S7-200PLC,配备EM235模拟量输入、输出模块,由PLC从启动开始,不断的输出数字量给EM235 的模块的AQW0,要求在50秒内使EM35的模拟量输出口I0输出电流从4ma开始线性增加到20 ma ,输送给电动阀门的输入控制端,使电动门在50秒内由关闭线性打开,直至全开。
EM235 的模块的AQW0的数字量赋值范围为0~32000,对应的模拟量输出为0~20ma,如输出为4~20ma,则对AQW0的数字量赋值应为6400~32000,数字量AQW0与输出电流的关系曲线如下图所示:
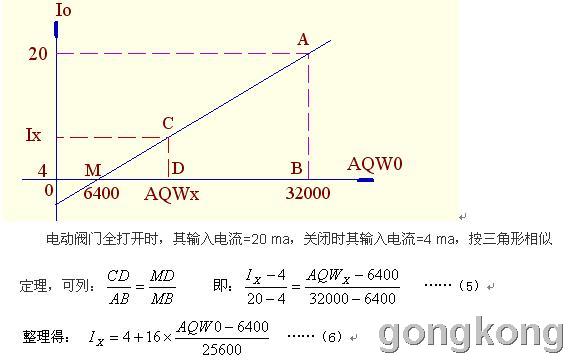
式(6)即为由数字量转换为电流量的转换公式:改变AQW0即改变EM235模拟量(电流)输出的大小,从而改变电动门的开门度。
编程构思:如以0.5秒间隔输送数字量给EM235的AQW0,则在50秒时间内可输出数据的次数=100, 可用S7-200的秒脉冲(SM0.5)的前后沿作为送数脉冲。
在50秒内,数字量的变化值=32000-6400=25600,则1秒的数字增量=25600÷100=256,则输送的数字量与时间T的关系式为: AQWx=6400+256*T ……(7)
下面即为用式(7)编写的在50秒内线性开门的梯形图:
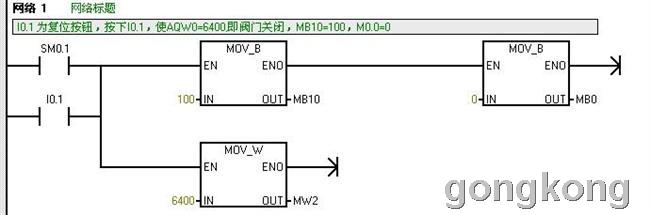
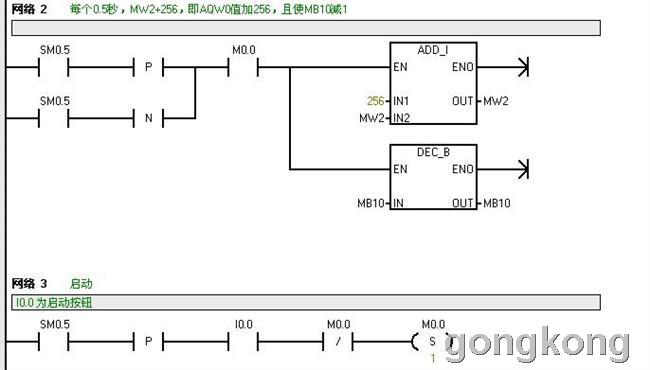
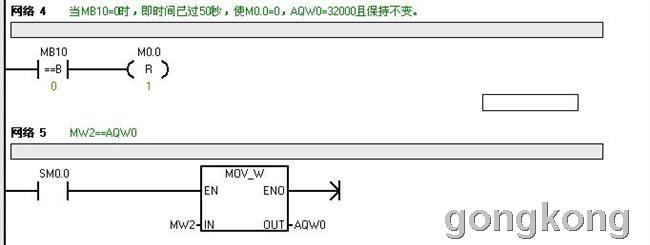
本文到此结束,如有不妥之处,请给予指正。谢谢大家!
- 数控机床故障诊断与维修实例
 [5655]
[5655] - 哪里有InTouch技术支持?
 [3372]
[3372] - wincc输入输出域如何输入负数...
 [3054]
[3054] - WinCC与Excel的互连
 [2179]
[2179] - 博图怎么使用电脑代替触触摸...
 [4048]
[4048] - 西门子LOGO230RC如何编程
 [3999]
[3999] - 急,请教exb文件用什么打开
 [2983]
[2983] - 组太王组合图素制图
 [2030]
[2030] - MCGS通用版的下拉框和选择框...
 [3413]
[3413] - TRACE MODE中国培训中心已于...
 [2415]
[2415]

官方公众号

智造工程师
-

 客服
客服

-

 小程序
小程序

-

 公众号
公众号






















 工控网智造工程师好文精选
工控网智造工程师好文精选
