【正运动技术】拱形运动在运动控制中的应用 点击:20 | 回复:0
在高速贴装行业中,常常会有非常多的高速抬升、平移、下降动作,常规的直角门型运动在直角拐角处为了降低机台震动,不得不进行减速停止,再重新加速的过程。
而拱形运动的优点在于:将直角拐弯处的运动轨迹处理成圆弧轨迹,不仅极大降低了减速程度,同时还保证了机台的稳定性,以及运动的连续性,提高了整体加工效率。
指令原型 ZAux_Direct_AutoCham(ZMC_HANDLE handle,float *PointA, float* PointB, float* PointC, float Cr ,int TableId, float* PointNum) 函数功能 自动计算空间倒角的关键点坐标 参数说明 参数名 描述 handle 连接标识 PointA 长度为3的一维数组,分别存储点A的xyz坐标 PointB 长度为3的一维数组,分别存储点B的xyz坐标 PointC 长度为3的一维数组,分别存储点C的xyz坐标 Cr 倒角半径 TableId table起始索引地址,数据运算的时候需要占用控制器的TABLE寄存器情况,TABLE(TableId)到TABLE(TableId+29) PointNum 空间圆弧的起始坐标(PointNum(0),PointNum(0+1),PointNum(0+2)) 空间圆弧的结束坐标(PointNum(0+3),PointNum(0+4),PointNum(0+5)) 空间圆弧的圆心坐标(PointNum(0+6),PointNum(0+7),PointNum(0+8)) 返回值 成功返回值为0,非0详见错误码说明 指令原型 ZAux_Direct_MSphericalABSSp(ZMC_HANDLE handle, int imaxaxises, int *piAxislist, float fend1, float fend2, float fend3, float fcenter1, float fcenter2, float fcenter3, int imode, float fcenter4, float fcenter5) 函数功能 绝对空间圆弧插补运动,SP运动方式 参数说明 参数名 描述 handle 连接标识 Imaxaxises 总轴数 piAxislist 轴列表数组 fend1 第1个轴运动距离参数1 Fend2 第2轴运动距离参数1 Fend3 第3个轴运动距离参数1 fcentre1 第1个轴运动距离参数2 Fcentre2 第2个轴运动距离参数2 Fcentre3 第3个轴运动距离参数2 imode 指定前面参数的意义 0 当前点、中间点、终点三点定圆弧: 距离参数1:为终点距离 距离参数2:为中间点距离 1 当前点、圆心、终点定圆弧,走最小的圆弧: 距离参数1:为终点距离 距离参数2:为圆心的距离 2 当前点、中间点、终点三点定圆: 距离参数1:为终点距离 距离参数2:为中间点距离 3 当前点、圆心、终点定圆,先走最小的圆弧,再继续走完整圆: 距离参数1:为终点距离 距离参数2:为圆心的距离 fcentre4 第4个轴螺旋距离 Fcentre5 第5个轴螺旋距离 返回值 成功返回值为0,非0详见错误码说明
指令原型 ZAux_Direct_SetForceSpeed(ZMC_HANDLE handle, int iaxis, float fValue) 函数功能 设置SP的运行速度 参数说明 参数名 描述 handle 连接标识 Iaxis 轴号 fValue 设置的速度值 返回值 成功返回值为0,非0详见错误码说明
拱形运动实现是将原本的门型运动里抬升、平移、下降三条直线插补,手动拆分成直线、圆弧、直线、圆弧、直线五条插补运动,再用连续插补来保证速度的连续性,这需要我们事先知道原门型运动的空间4点坐标,将直角轨迹改成圆弧轨迹。
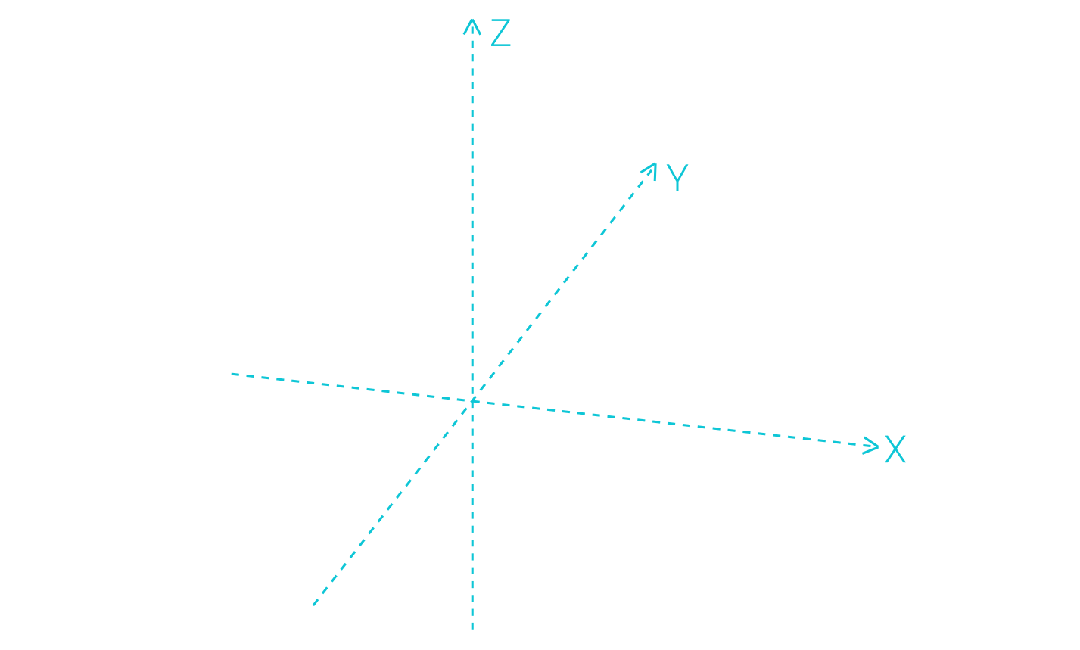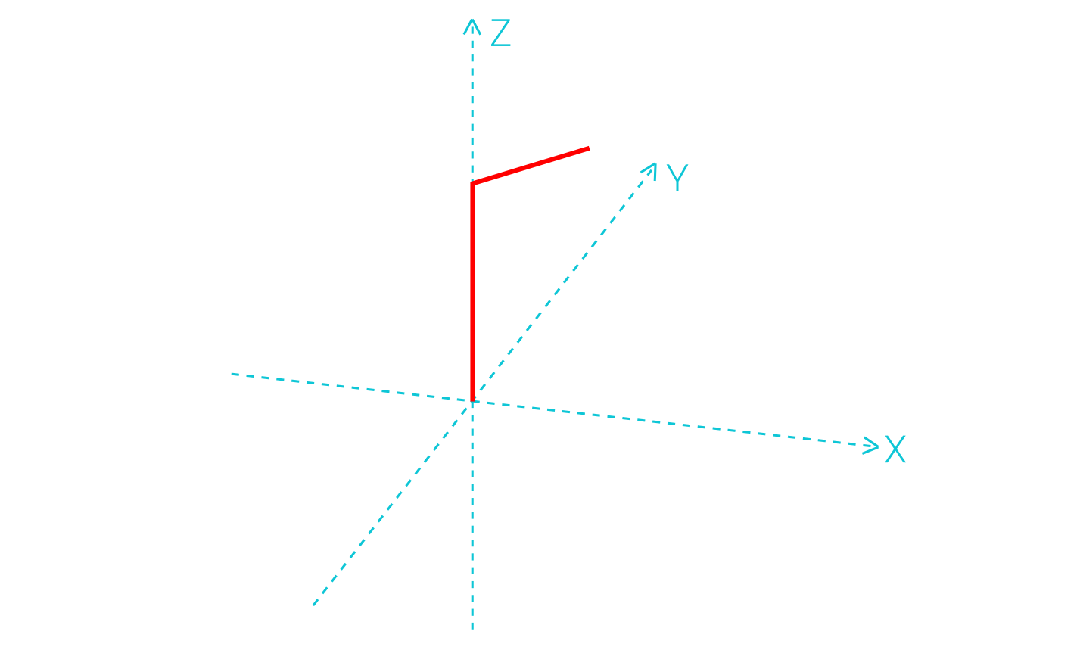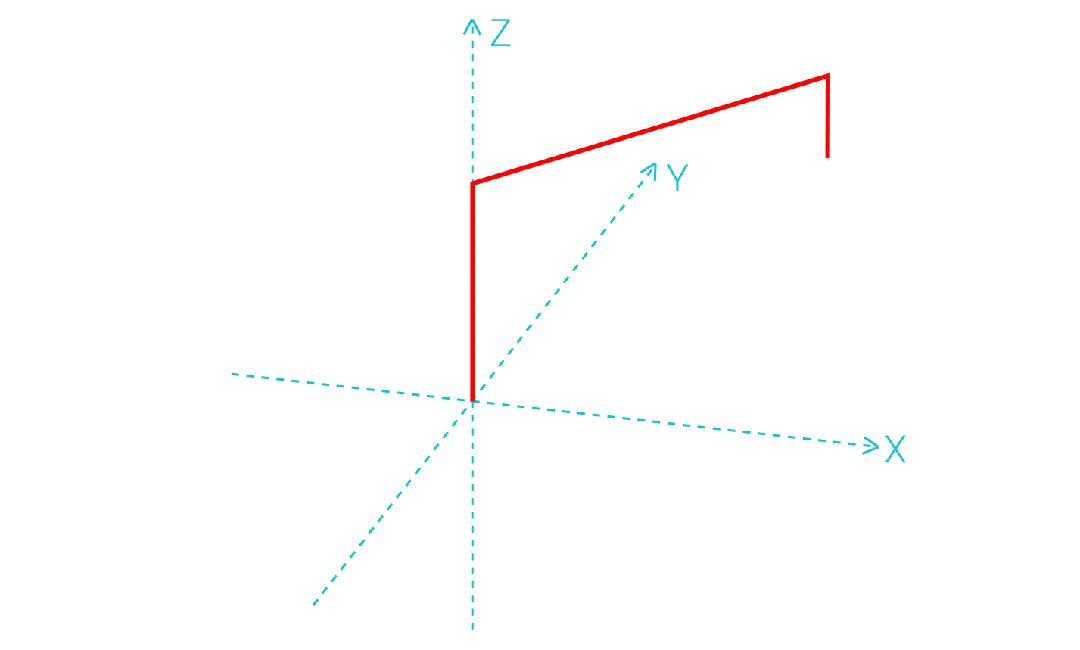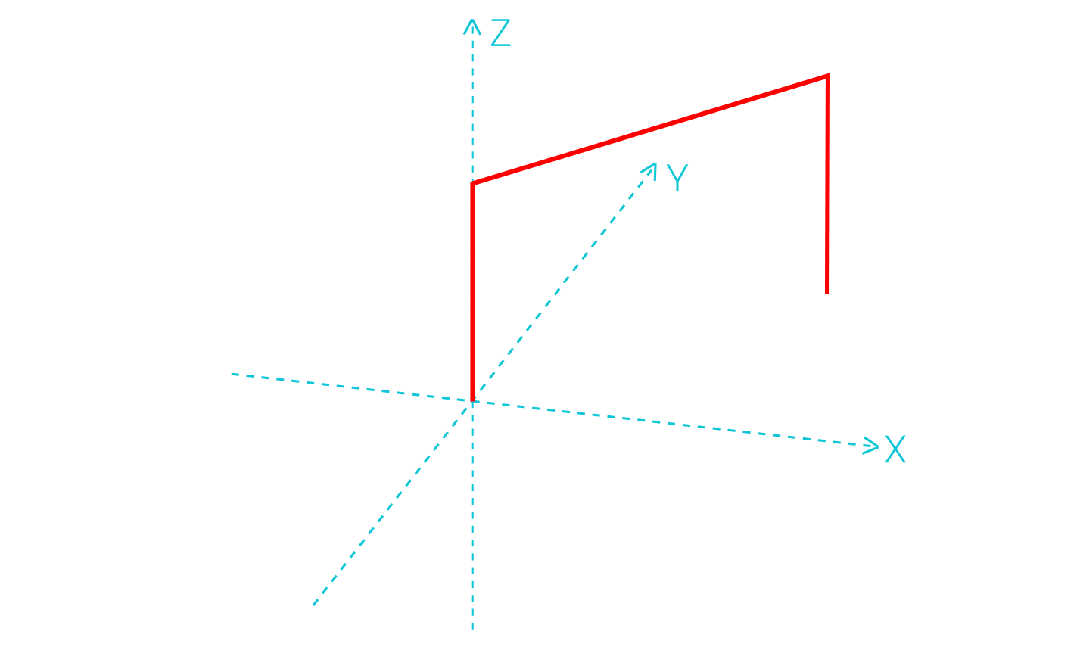
1.门型运动轨迹
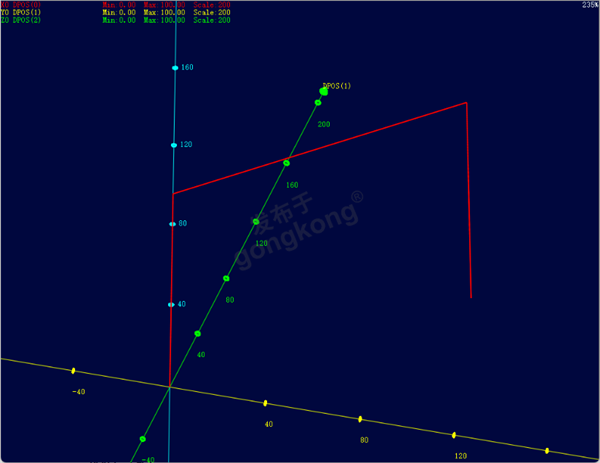
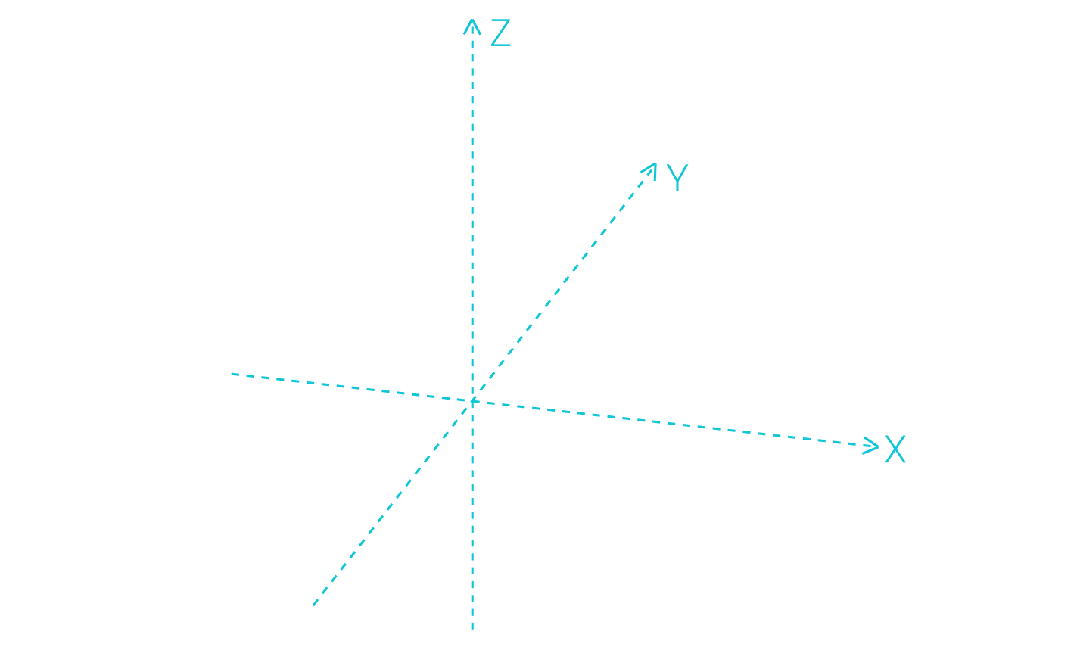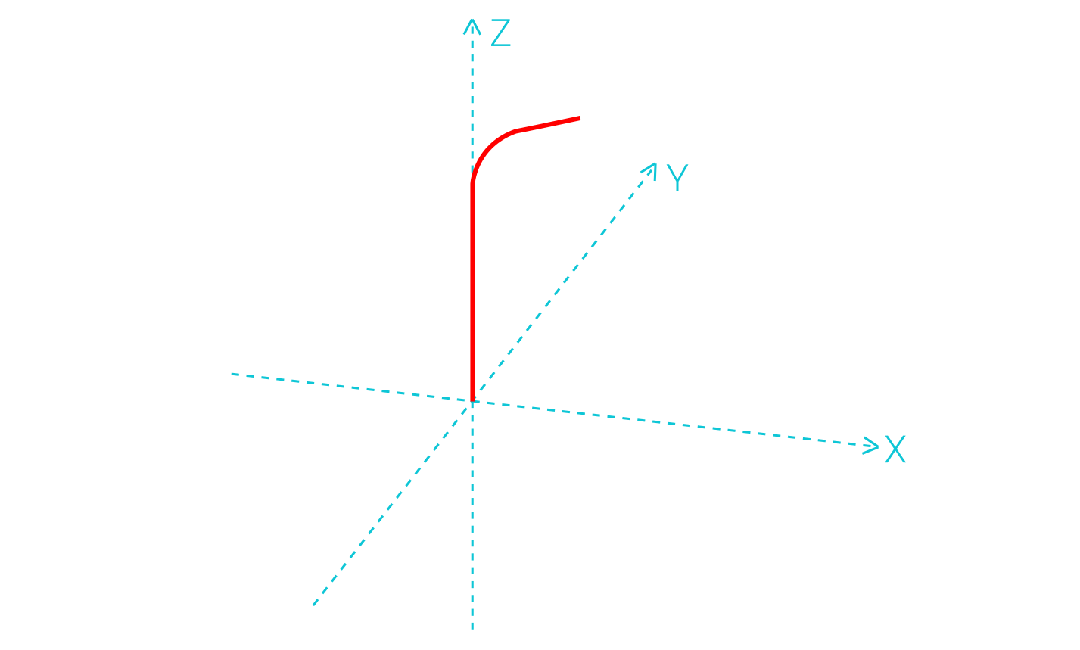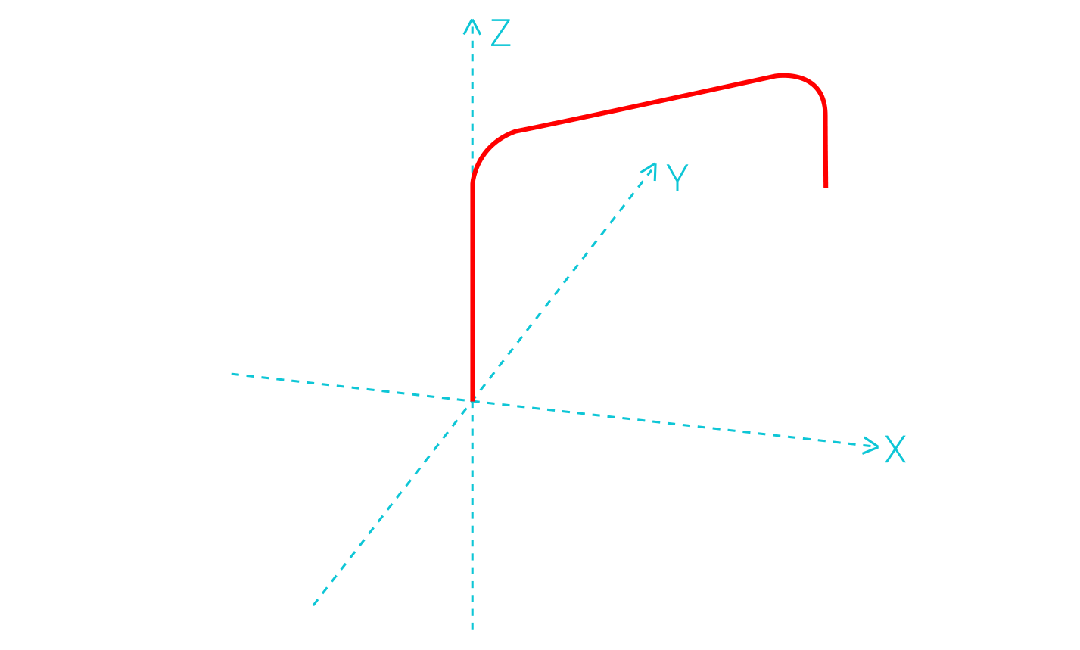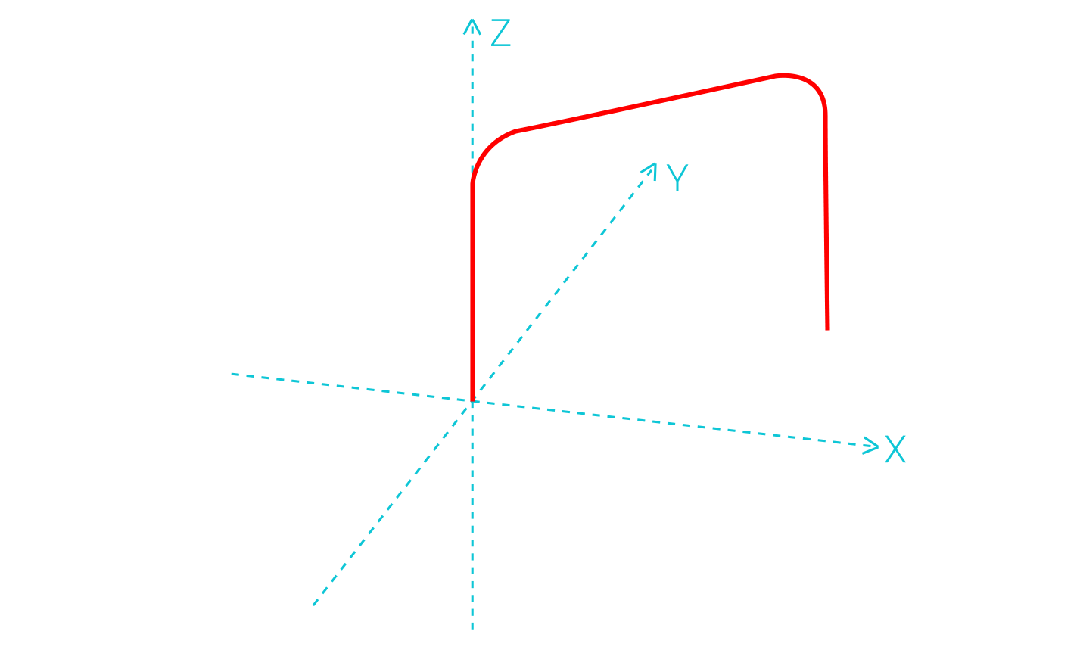
2.拱形运动轨迹
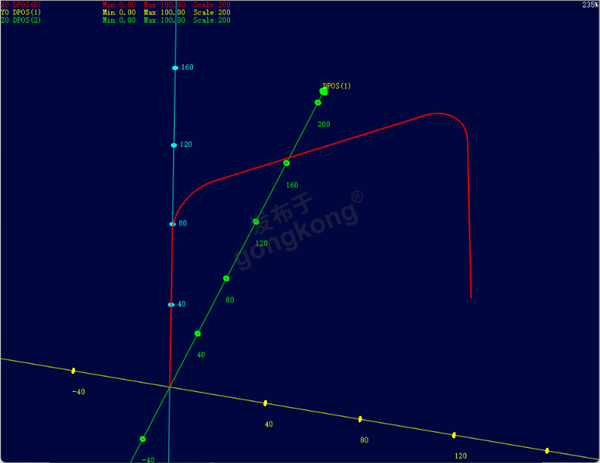
楼主最近还看过






 工控网智造工程师好文精选
工控网智造工程师好文精选
