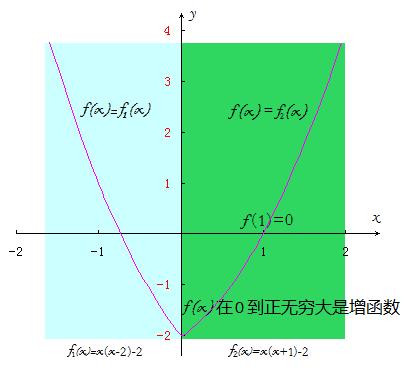
对于19楼所例举的函数 f(x)=x-ln[(1+x)/2]-1 来说，当(f(x)-f(-x))/x＜0时x的范围是 { x│x∈(-1，1) 且x≠0 }

　　由函数解析式f(x)=x-ln[(1+x)/2]-1可以看出：此函数的定义域为(-1，+∞)，

　　当(f(x)-f(-x))/x＜0时，x的范围是{ x│x∈(-1，1) 且x≠0 }。

　　请大家注意：在函数f(x)=x-ln[(1+x)/2]-1的定义域(-1，+∞)内，当自变量x的取值在[1，+∞)区间上时，x的相反数“-x”落在了f(x)=x-ln[(1+x)/2]-1的定义域之外，当然也就没有对应的“函数值f(-x)”。

　　所以，该函数在[1，+∞)区间上，使题目核心部分的不等式“(f(x)-f(-x))/x＜0”没有意义！

　　因此，该函数当(f(x)-f(-x))/x＜0时，x的范围只能在“-1＜x＜1   且x≠0”! 如图中有淡蓝底色的部分所示。

　　有空了，把第17楼例举的函数 f(x)＝f1(x)=x(x-2)-2  (当自变量值＜0时)；

f(x)＝f2(x)=x(x+1)-2  (当自变量值≥0时) . 的数据图表补充详细一点：

　　由函数解析式f(x)=f1(x)=x(x-2)-2  (当自变量值＜0时)；f(x)=f2(x)=x(x+1)-2  (当自变量值≥0时) 可以看出：此分段函数的定义域为(-∞，+∞)，

　　对于该分段函数f(x)来说，当(f(x)-f(-x))/x＜0时，x的范围是除0之外的一切实数。

　　函数f(x)=3x^4-8x^3+6x^2-1 . 的定义域是(-∞，+∞)

　　下面用一组具体的数据抽查检验函数f(x)=3x^4-8x^3+6x^2-1 .　符合题目的情况：

　　对于函数f(x)=3x^4-8x^3+6x^2-1 来说，当(f(x)-f(-x))/x＜0时，x的范围是除0之外的一切实数。

　　再把19楼所例举的函数 f(x)=x-ln[(1+x)/2]-1 曲线与数据表结合起来：

　　函数 f(x)=x-ln[(1+x)/2]-1 的定义域是(-1，+∞)。当自变量x在[1，+∞)上取值时，x的相反数“-x”就落在了函数“ f(x)=x-ln[(1+x)/2]-1”的定义域之外啦，这时函数 f(x)=x-ln[(1+x)/2]-1 在对应的“-x”上就没有定义！也就在开区间(-1 ，1)之外使题目核心部分的那个不等式“(f(x)-f(x))/x＜0”缺失计算的依据！从而在开区间

(-1 ，1)之外使不等式“(f(x)-f(x))/x＜0”没有意义！

　　对于函数 f(x)=x-ln[(1+x)/2]-1 来说，当(f(x)-f(-x))/x＜0时，x的范围只能是　

“-1＜x＜1   且x≠0”! 如图中有淡蓝底色的部分所示。

　　请网友们注意：

　　符号“f(-x)”是人们在研究函数的奇偶性问题时引入的一个函数值符号！在函数f(x)的定义域内，如果存在“互为相反数”的“x”和“-x”，那么，自变量取值为与“x”相反的数“-x”时所对应的函数值就是“f(-x)”!

　　老王出示一下正统教科书上的图片资料：（老王以正统教科书上的理论为依据来发言）  

　　图1-11(a)中，点A的坐标为(x，f(x))，点A' 的坐标为(-x，f(-x))；

　　图1-11(b)中，点A的坐标为(x，f(x))，点A'' 的坐标为(-x，f(-x))；

　　函数曲线上的点的坐标(x，y)，其横坐标为“自变量值”，纵坐标为对应的“函数值”！

　　我们研究函数的“奇偶性”，并不等于说我们所研究的函数f(x)非奇则偶！因为函数f(x)除了奇函数、偶函数之外，还有非奇非偶的函数。

　　譬如，判断函数f(x)=x^3+x^(-1/3)是否具有奇偶性：

　　根据此例函数f(x)的对应法则f( )=( )^3+( )^(-1/3)可知该函数f(x)的定义域是x∈R，且x≠0 ，所以该函数f(x)的定义域是关于实数“0”对称的，自变量的任意一个非零取值x，在函数定义域内都有其对应的相反数“-x”存在，故在该函数f(x)的值域内都有其对应的“函数值 f(-x)”存在.

　　解：利用函数值f(-x)去考察该函数是否具有奇偶性，把“-x”代入该函数的对应法则 f( )=( )^3+( )^(-1/3) 得：

　　　f(-x)=(-x)^3+(-x)^(-1/3) = -x^3 －x^(-1/3)= -(x^3+x^(-1/3))

　　　即：f(-x)= -f(x) 　　所以，f(x)=x^3+x^(-1/3)　是奇函数.　

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　又譬如，判断函数f(x)=2x^4+3x^2 是否具有奇偶性：

　　根据此例函数f(x)的对应法则f( )=2( )^4+3( )^2可知该函数f(x)的定义域是x∈R，所以该函数f(x)的定义域是关于实数“0”对称的，自变量的任意一个非零取值x，在函数定义域内都有其对应的相反数“-x”存在，故在该函数f(x)的值域内都有其对应的函数值“f(-x)”存在.　　

　　解：利用函数值f(-x)去考察该函数是否具有奇偶性，把“-x”代入该函数的对应法则 f( )=2( )^4+3( )^2 得：

　　　　f(-x)=2(-x)^4+3(-x)^2=2x^4+3x^2   

　　即：f(-x)=f(x)  　　所以，f(x)=2x^4+3x^2 是偶函数.

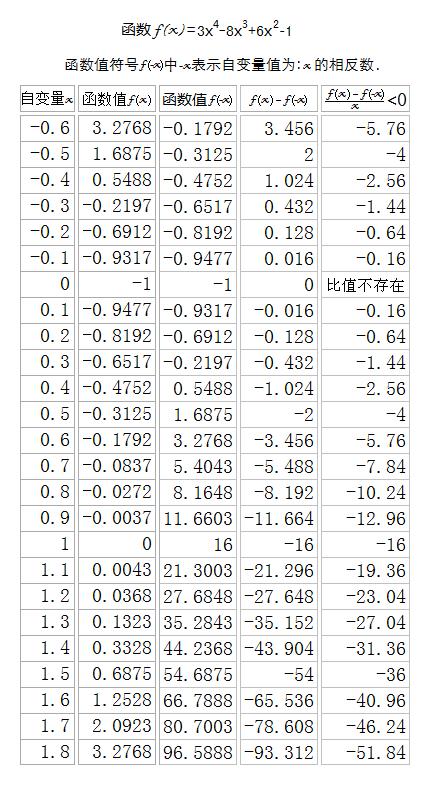
　　再譬如，判断函数f(x)=3x^4-8x^3+6x^2-1 是否具有奇偶性：

　　根据此例函数的对应法则f( )=3( )^4-8( )^3+6( )^2-1 可知函数f(x)的定义域是x∈R 。所以，该函数f(x)的定义域是关于实数“0”对称的，自变量的任意一个非零取值x，在函数定义域内都有其对应的相反数“-x”存在，故在该函数f(x)的值域内都有其对应的“函数值 f(-x)”存在.　

　　解：利用函数值f(-x)去考察该函数是否具有奇偶性，把“-x”代入该函数的对应法则 f( )=3( )^4-8( )^3+6( )^2-1 得：

　　f(-x)=3(-x)^4-8(-x)^3+6(-x)^2-1＝3x^4+8x^3+6x^2-1

　　∵ 3x^4+8x^3+6x^2-1≠ -(3x^4-8x^3+6x^2-1)　∴ f(-x)≠ -f(x)

　又∵ 3x^4+8x^3+6x^2-1≠3x^4-8x^3+6x^2-1　　∴  f(-x)≠ f(x)

　　所以，函数f(x)=3x^4-8x^3+6x^2-1 　既不是奇函数，也不是偶函数。

　　我们就说：函数f(x)=3x^4-8x^3+6x^2-1 不具有奇偶性。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

　　还譬如，判断函数f(x)=x-ln[(1+x)/2]-1是否具有奇偶性：

　　解：函数f(x)＝x-ln[(1+x)/2]-1的定义域为(-1，+∞) ，所以，其定义域(-1，+∞)内的半开区间[1，+∞)上任意一个取值“x”，其相反数“-x”都落在了定义域

(-1，+∞)之外，那么，函数f(x)＝x-ln[(1+x)/2]-1就不具有 (关于原点或y轴) 的对称性！

　　所以，函数f(x)＝x-ln[(1+x)/2]-1 既不是奇函数，也不是偶函数。

　　即：函数f(x)＝x-ln[(1+x)/2]-1 不具有奇偶性！

　　函数f(x)=x-ln[(1+x)/2]-1在定义域 (-1，+∞) 内自变量取值存在有互为相反的数的范围是开区间(-1，1)。

　　如果把对f(x)=x-ln[(1+x)/2]-1的考察范围局限在开区间(-1，1)上，那么，我们也可以利用“函数值f(-x)”来判断函数f(x)=x-ln[(1+x)/2]-1在开区间(-1，1)上是否具有奇偶性：

　　把“-x”代入题设函数的解析式f(x)=x-ln[(1+x)/2]-1 得：

　　f(-x)=(-x)-ln((1+(-x))/2)-1= -x-ln((1-x)/2)-1= -( x+ln((1-x)/2)+1)

 　　∵ -( x+ln((1-x)/2)+1)≠ -( x-ln((1+x)/2)-1) 　　 即： f(-x)≠ -f(x) 

　　所以，函数f(x)=x-ln[(1+x)/2]-1在开区间(-1，1)范围内也既不是“奇函数”；

　　又∵ - x-ln[(1-x)/2]-1≠ x-ln[(1+x)/2]-1　　　　 即： f(-x)≠f(x)

　　所以，函数f(x)=x-ln[(1+x)/2]-1在开区间(-1，1)范围内照样也不是“偶函数”.

　　所以我们说：

　　即便把考察范围局限在开区间(-1，1)上，函数f(x)=x-ln[(1+x)/2]-1 仍然也不具有奇偶性。

　　一般地，对于函数f(x)：　　 

　　1、如果对于函数定义域内任意一个x，都有f(-x)= - f(x)，那么函数f(x)就叫做奇函数。　　

　　2、如果对于函数定义域内任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。　　 

　　3、对于函数定义域内任意一个x，若有f(-x)≠ - f(x)，且f(-x)≠f(x)，那么函数f(x)既不是奇函数，也不是偶函数！此种情况我们就说函数f(x)不具有奇偶性。  

　　4、对于函数定义域内任意一个x，若其相反数“-x”都落在定义域之外，那么该函数的值域内就绝无“函数值f(-x)” ! 

　　所以，该函数f(x)也就绝无（关于y轴或原点的）对称性可言！该函数f(x)也当然的既不是奇函数，也不是偶函数！此种情况当然是函数不具有奇偶性的情况！

　　譬如：对于函数f(x)=logax ，定义域是x＞0 ，自变量的任意一个取值x，其相反数“-x”都落在定义域之外，那么，对数函数f(x)=logax 的值域内就绝无“函数值f(-x)”，即绝无“函数值loga(-x)”！

　　所以，对数函数f(x)=logax 是“非奇非偶”的函数！对数函数f(x)=logax 不具有奇偶性！ 　　　   

　　虽然，符合该题目之“f(x)在0到正无穷大是增函数，f(1)=0”条件的函数是很多的、数不胜数的，但是，对数函数 f(x)=logax  却不符合“f(x)在0到正无穷大是增函数”！因为对数函数 f(x)=logax 在“x=0”处没有定义！

　　大家都知道：“0”没有对数。即“loga0”没有意义！

　　“在0到正无穷大”即指半开区间“[0，+∞)”，而对数函数f(x)=logax 的定义域是开区间(0，+∞)。

　　这“开区间(0，+∞)”并不等于“半开区间[0，+∞)”!

　　高中学生都知道：半开区间[0，+∞)大过开区间(0，+∞)！　

　　而且，对数函数 f(x)=logax  (a＞0，且a≠1)定义域(0，+∞)内任意一个自变量值x，其相反数“-x”都落在定义域之外，即“负数没有对数”。

　　所以，在对数函数 f(x)=logax  (a＞0，且a≠1) 的值域内绝无“函数值f(-x)”存在！

　　即： 对数函数 f(x)=logax  让题目核心部分的那个不等式“(f(x)-f(-x))/x＜0”在整个定义域范围都绝不可能有获得成立的条件，从而使题目无解！

　　所以，对于<研讨会宣传员-3259>所给题目，刘志斌用对数函数f(x)=logax 来解，是明显错误的！