今天想加大点难度，提供了两年的销量（希望让Deep Seek根据两年的销售量可以计算每年的增长比例，每个月的季节因子），然后根据季节因子预测2025年的销量。

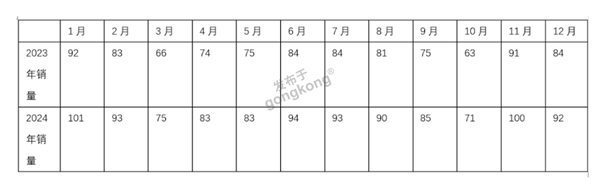
Deep Seek的预测结果:

在季节性波动预测中整合历史数据的影响时，可通过以下步骤进行系统分析：

1. 数据准备与趋势分析

• 计算年度增长趋势：

• 2023年总销量：92 + 83 + ... + 84 = 972

• 2024年总销量：101 + 93 + ... + 92 = 1077

• 增长率：(1077 - 972) / 972 ≈ 10.8%

• 趋势外推：假设线性增长，预计2025年总销量为 1077 * 1.108 ≈ 1194。

• 月度趋势校正：若增长不均衡（如某些月份增幅更高），需单独拟合线性/非线性趋势模型（如移动平均、指数平滑）。

2. 季节性指数计算

• 计算每月平均销量（取两年均值）：

  月份	1月	2月	...	12月
  均值	96.5	88.0	...	88.0

• 计算季节性指数（各月均值占全年平均的百分比）：

• 全年均月销量：(972 + 1077) / 24 ≈ 85.375

• 示例（1月）：96.5 / 85.375 ≈ 113%

• 结果：每个月份对应比例即为季节指数（如1月为旺季指数113%，某些月份可能低于100%）。

3. 预测模型构建

模型选择与步骤

• Holt-Winters三参数指数平滑：

• 水平（L）：基础销量

• 趋势（T）：增长速率

• 季节（S）：周期性波动

• 公式（乘法模型）：
  $\text{预测值} = (L + T) \times S$

• SARIMA模型：
  利用(p,d,q)(P,D,Q,s)参数捕捉趋势和季节性（s=12为年度周期）。

• 回归分析：
  $$\text{销量} = \beta_0 + \beta_1 t + \sum_{i=1}^{11} \alpha_i \text{Month}_i$$

• $t$：时间变量（趋势项）

• $\text{Month}_i$：月份虚拟变量（季节性）

4. 预测值生成

以 2025年1月销量预测 为例：

• 趋势外推：基于年均增长10.8%，预计2025年1月趋势值为 101 * 1.108 ≈ 112。

• 应用季节指数：1月季节指数113%，调整后预测值为 112 * 1.13 ≈ 127。

5. 历史数据权重的优化

• 时间衰减权重：为近期数据分配更高权重（如2024年数据权重为0.6，2023年为0.4）。

• 动态调整：根据残差分析优化季节性指数，确保模型适应变化（如促销活动导致的模式偏移）。

注意事项

• 数据局限性：仅两年数据可能导致季节性估计偏差，建议积累≥3年数据。

• 外部因素：若存在节假日、政策等干扰，需在模型中增加协变量。

通过以上方法，历史数据的趋势和季节性特征可被有效整合，提升预测的准确性。

来源：微信号xuyongshuo-work

作者：许永硕

该作品已获作者授权，未经许可，禁止任何个人及第三方转载。